Tarjan

Tarjan

前言

Tarjan算法主要能解决两类问题：

1. 强连通分量和双连通分量
2. 割点与桥

强连通分量

题目

题目传送门

什么是强连通分量

强连通

$x,y$ 强连通 等于 $x$ 能到 $y$, $y$ 也能到 $x$.

强连通图

$\forall x,y\in G$ 都有 $x,y$ 强连通，则称 $G$ 为强连通图

强连通子图

$\forall x,y\in G^{\prime }$ 并且 $G^{\prime }\subseteq G$，$x,y$ 都强连通，

强连通分量

极大的强连通子图

---

作用

1. 减小时间复杂度
2. 将有向图进行缩点转换成有向无环图

---

原理

Tarjan算法有两个重要数组：

1. dfn[i]：表示走到这个点所花的时间。
2. low[i]：表示i这个节点所能走到的小时间戳。

除此之外，还需定义一个栈（$st[]$）和一个染色数组（$col[]$），详细作用看代码。

其中有几种不同的边：

1. $红边$ 代表树边，只需更新当前节点的 $low$ 值，即low[x] = min(low[x], low[y]);。
2. $蓝边$ 代表横插边, 因为y已经遍历过了，所以啥都不用干。
3. $绿边$ 代表返祖边，也是只要更新$low$ 值，即low[x] = min(low[x], dfn[y])（或者改为low[x] = min(low[x], low[y]), 只不过是为了模板统一起见）。

最后如何知道这是一个强连通分量呢？其实很简单，只要回溯时判断一下当前这个节点的dfn[i] 是否等于 low[i] 即可。

由于较抽象，所以举个栗子, 设一张图为：

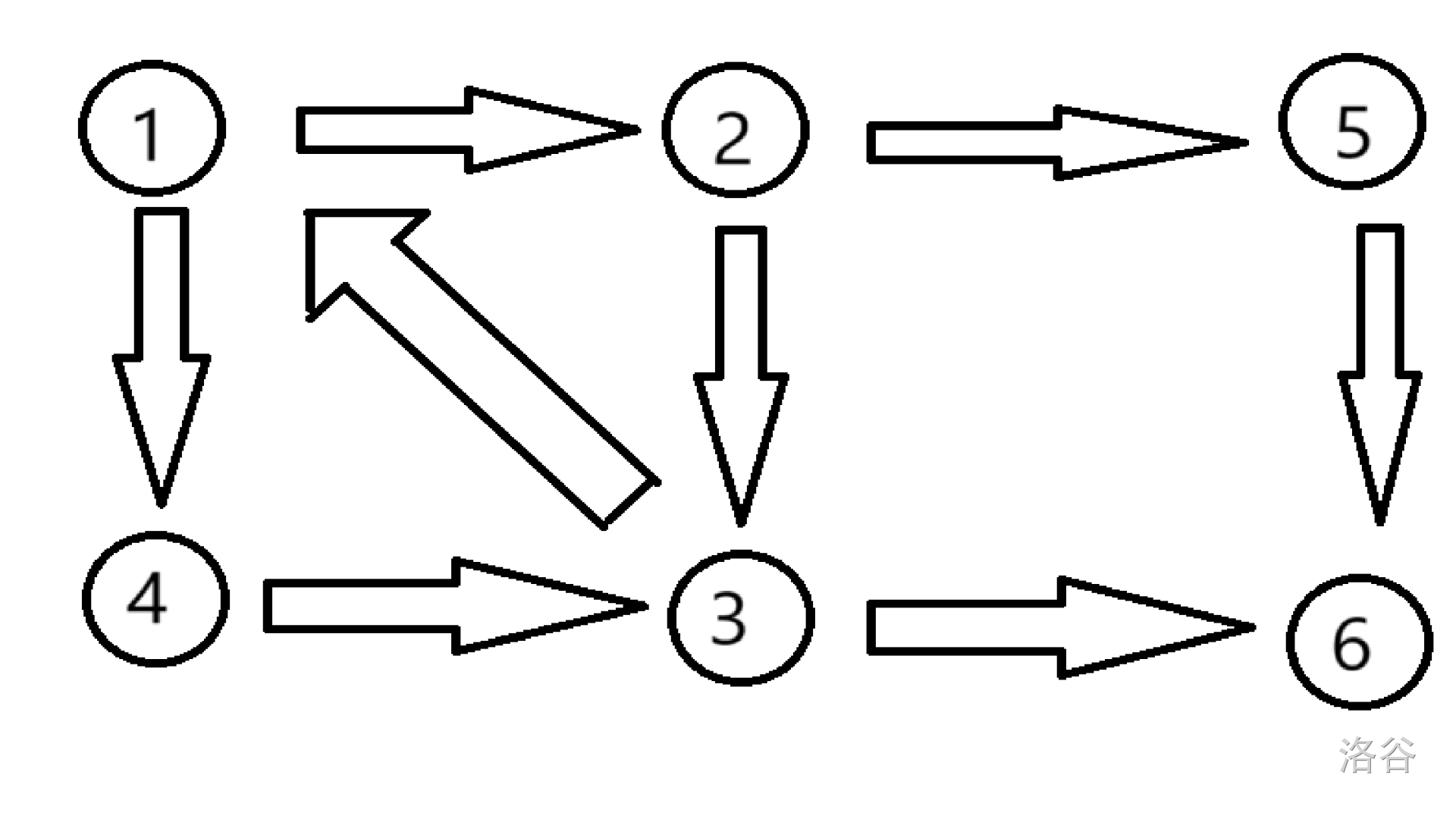
假设从1开始搜，则，它的搜索树为：

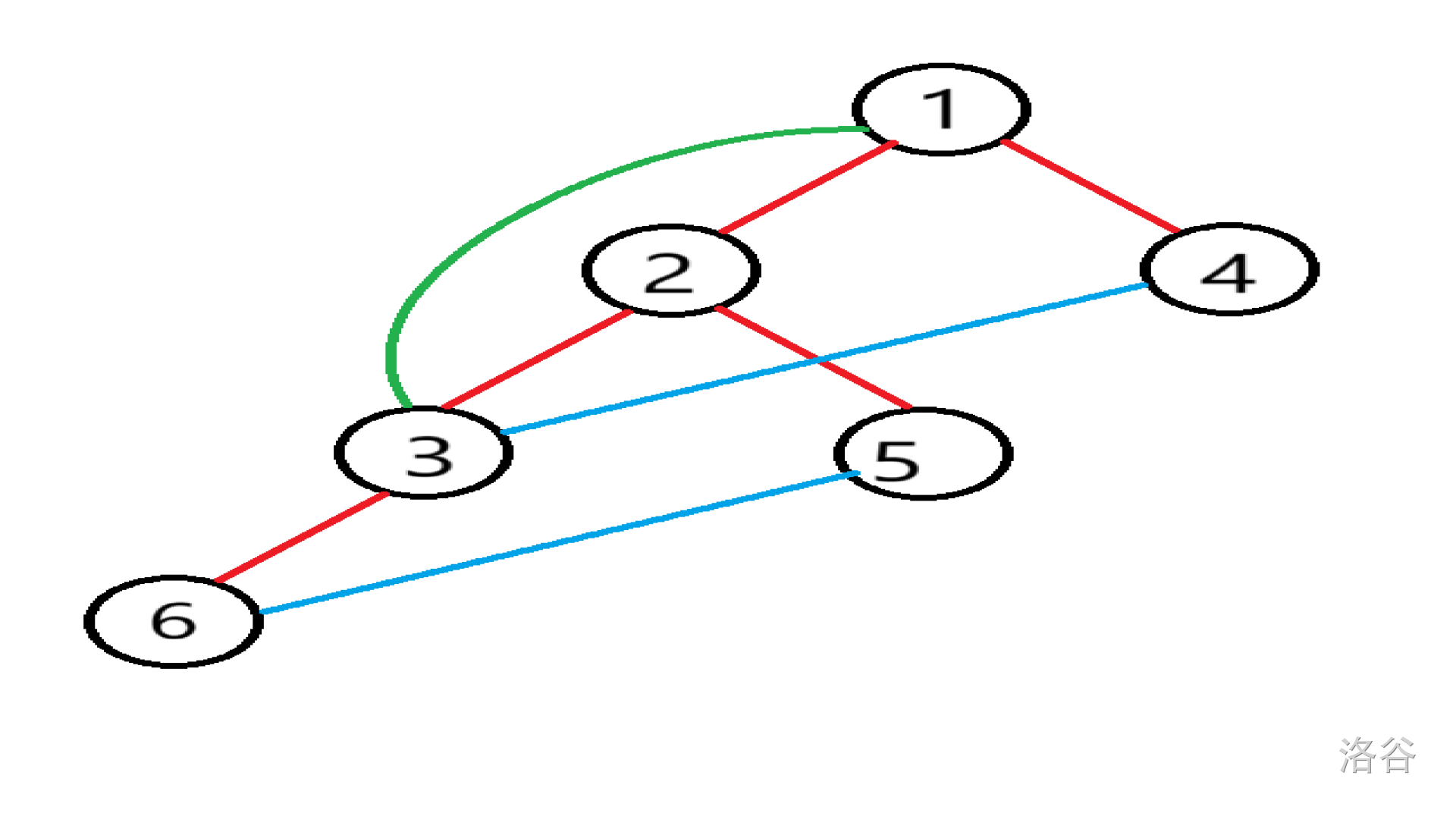
设该递归函数为Tarjan

• 遍历到①，则dfn[1] = low[1] = ++t(1)，①的所指向的节点有②，④，假设下次遍历②，先调用Tarjan(2)再low[1] = min(low[1], low[2])，此时栈为①.

• 遍历到②，则dfn[2] = low[2] = ++t(2)，②的所指向的节点有③，⑤，假设下次遍历③，先调用Tarjan(3)再low[2] = min(low[2], low[3])，此时栈为①，②.

• 遍历到③，则dfn[3] = low[3] = ++t(3)，③的所指向的节点有①，⑥，假设下次遍历①，但是①以前已经被遍历过了，且①还在栈中，即为返祖边，low[3] = min(low[3], dfn[1])就可以了，此时栈为①，②，③.

• 除此之外，③还有一个子节点⑥，dfn[6] = low[6] = ++t(4)只要更新一下 $low$ 即可，但是⑥回溯时就会发现dfn[6] == low[6], 所以⑥出栈，再将⑥染色，即col[6] = sz.

• 回溯到②，②也还有一个子节点⑤，更新low[2] = min(low[2], low[5])即可.

• 遍历到⑤，发现⑤只有一条边，且连向的这个节点已经染过色了，即为横插边，无需考虑，但是⑤的$low[5]$ 等于 $dfn[5]$，所以需要染色并出栈，此时栈为：①，②，③.

• 遍历到④，更新 $low$ 即可.

• 回溯到①，因为low[1] == dfn[1]，所以要将所有 $low$ 值为 $low[1]$ 的元素出栈，将其染色，需染色的元素即为：①，②，③，④.

代码

void Tarjan(int x) {
	dfn[x] = low[x] = ++t;
	st[++top] = x;
	for (auto y : g[x])
		if (!dfn[y]) { // 树边
			Tarjan(y);
			low[x] = min(low[x], low[y]);
		} else if (!col[y]) low[x] = min(low[x], dfn[y]); // 返祖边
		// 横插边不用考虑
	if (low[x] == dfn[x]) {
		int cnt = 0;
		++sz, ++top;
		// 颜色种类多一，因为当st[top] == x时也是强连通分量的一个节点，所以top要加一
		while (st[top--] != x) {
			col[st[top]] = sz;
			cnt++; // 强连通分量的节点个数加一
		}
		if (cnt > 1) ans++; // 如果只有一个节点，不满足题目要求
	}
}

割点与桥

割点

题目

题目传送门

什么是割点

割点的定义：去掉这个点，会使图的连通块增加（只针对无向图）。

举个例子：

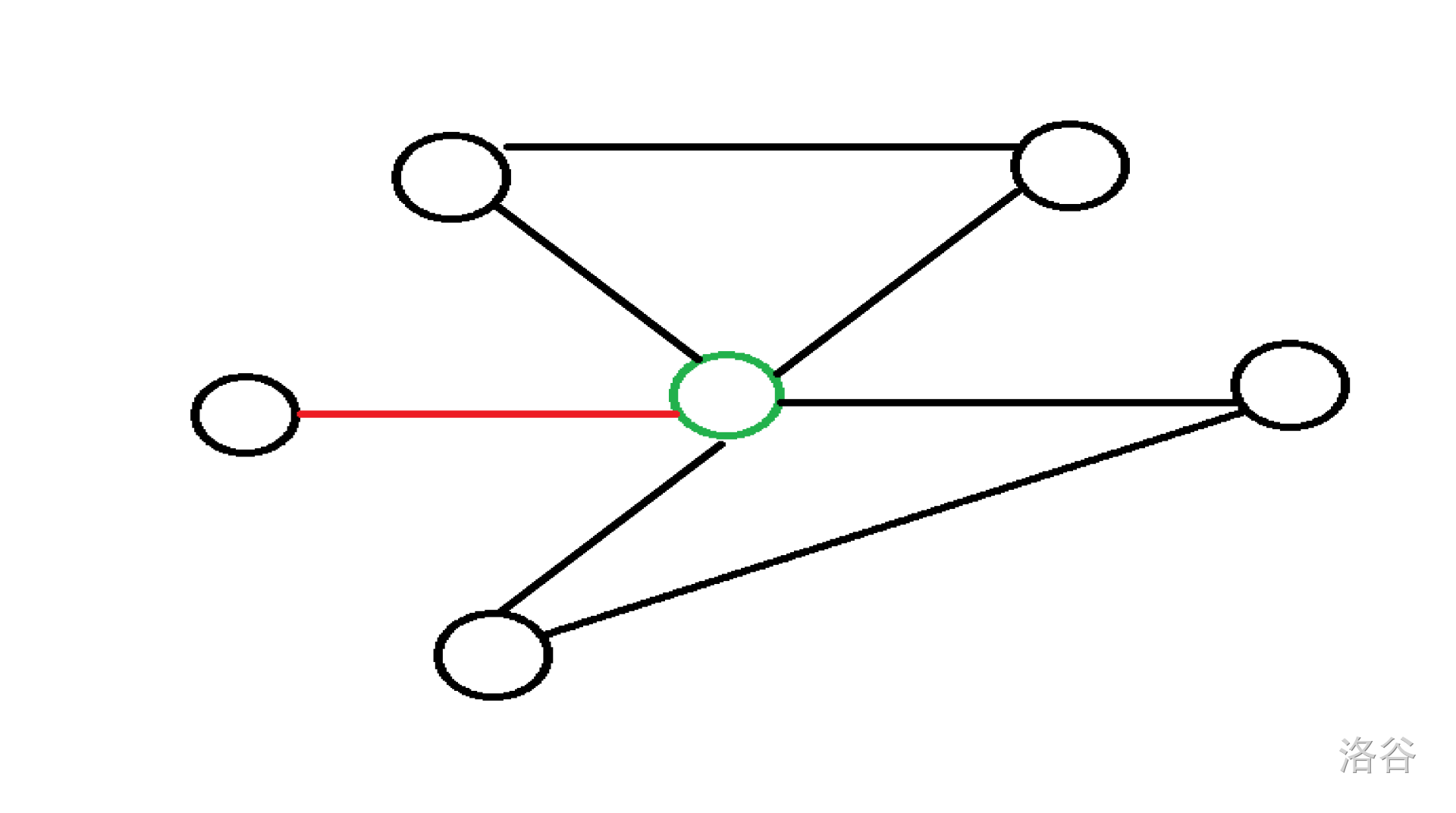
绿色的点就是割点，因为他可以将整个图分成三个部分，而其他点都不行。

原理

与强连通分量不同，因为将有向图改为了无向图，有一些性质是会变的：

1. 有向图分成三种边：树边、返祖边和横插边，而无向图只有两种边：树边和返祖边，考虑下面的图：

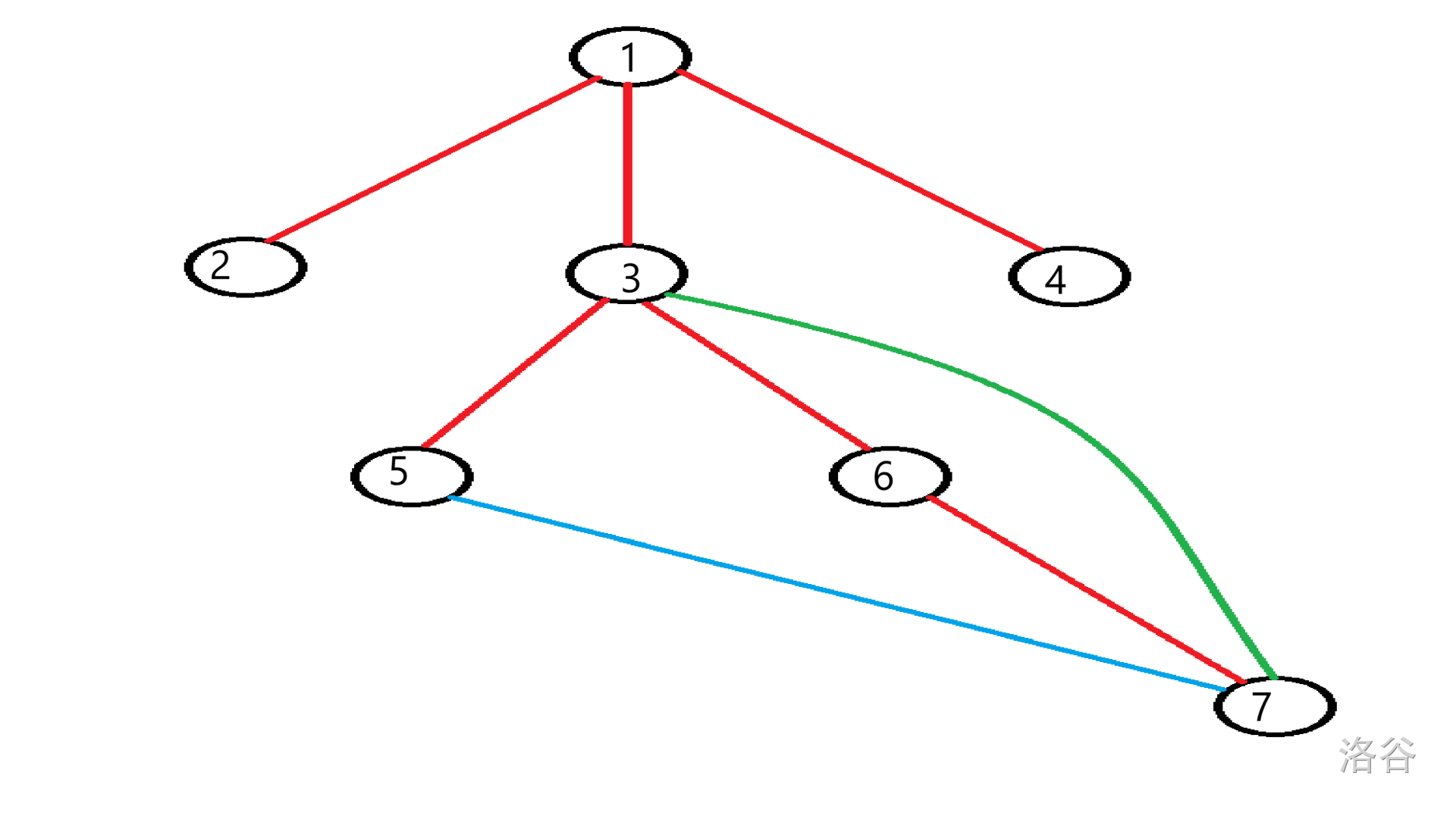
还是一样的：

• $红边$ 代表树边。
• $蓝边$ 代表横插边。
• $绿边$ 代表返祖边。

虽然开上去很合理，实际上在递归搜索是会先搜③⑤⑦⑥，再变成③⑥和③⑦为返祖边。

图是这样的：

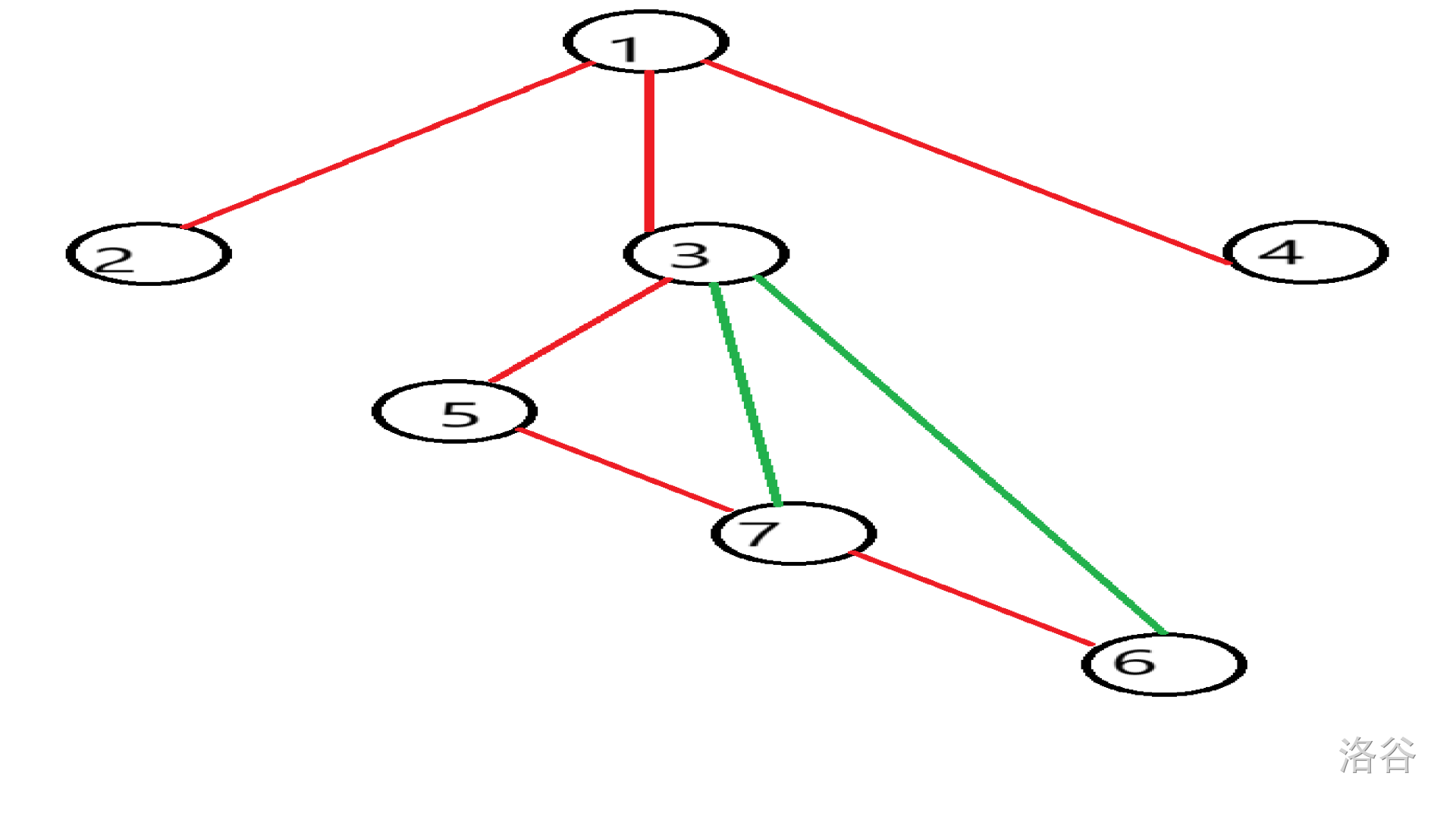
2. 割点虽然也有两个数组 low[i] 和 dfn[i]，但是 low 数组的定义稍微不同：low[i]：表示不经过其父亲节点的点与其子节点能到的最小时间戳。
3. 最后，割点不用另外开一个栈。

所以，割点的代码会比强连通分量的代码好写些。。。

假设枚举到了 $x$ 这个点，其子节点为 $y$，如下图：

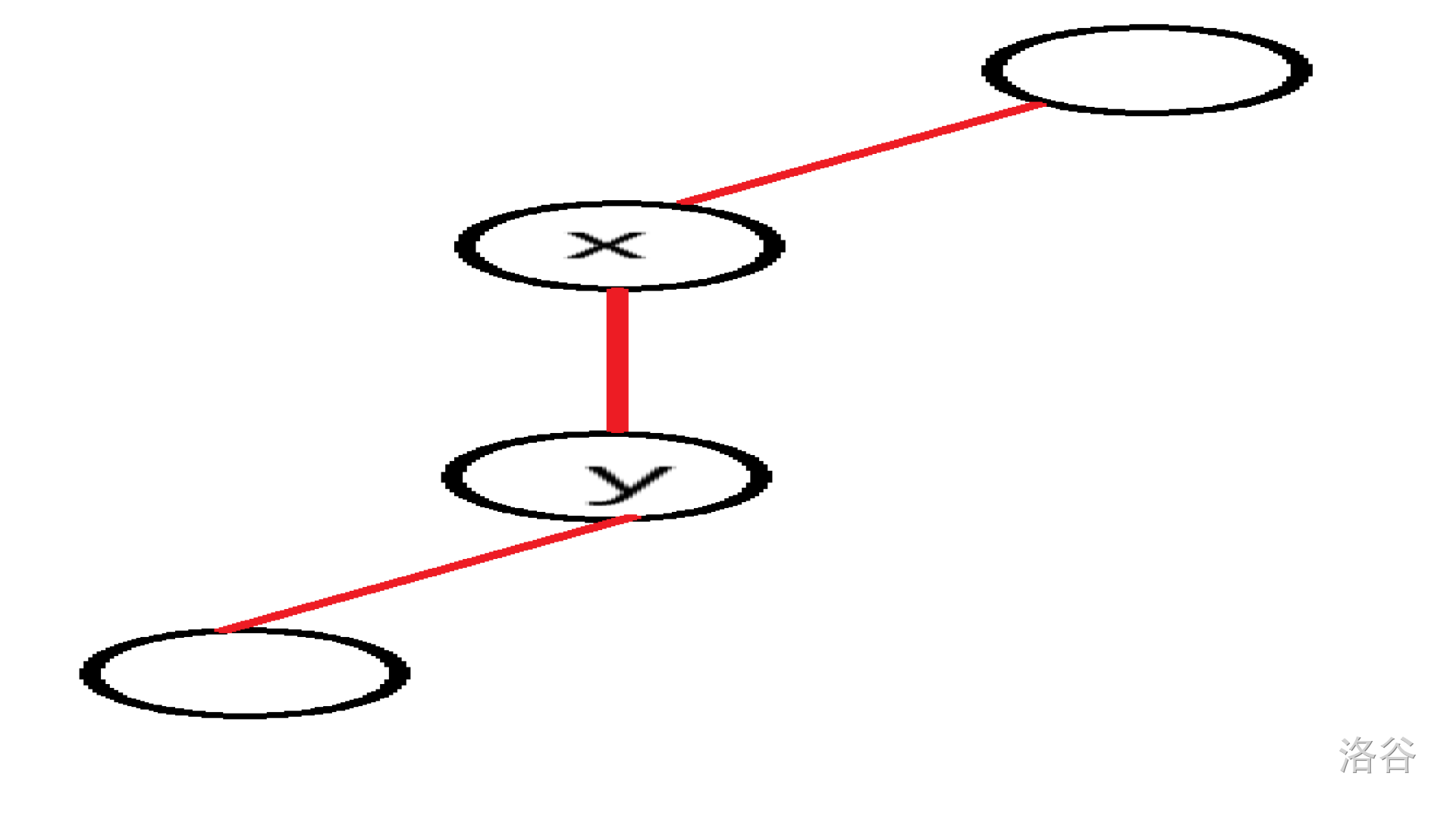
显然，$x$ 和 $y$ 都为割点，可是要在什么情况下 $x$ 不是割点呢？要想他不是割点，那么当 $x$ 去掉后还是只有一个连通块，即在搜索树的情况下是在 $x$ 这个点下边的点有至少一个节点连向了 $x$ 这个点的上方的点，即在 $x$ 下方至少有一个点与 $x$ 上方的点有一条返祖边（不能连向 $x$ 本身），但是还有一个特殊情况：当 $x$ 为根节点是上方是没有点的，设 $x$ 有 $cnt$ 个子节点：

• $cnt=1$：去掉这个点并没有影响。
• $cnt>1$：$x$ 成为割点。

最后，因为我们一般存图是 $u$ -> $v$建一条边，再建一条 $v$ -> $u$ 的边，知道了这些，就可以进行下面的处理了。

若$x$ 为割点，即上图所示，此时的 dfn[x] = 2, low[x] = 1(因为有一条连向节点 $1$ 的边)，同理，dfn[y] = 3, low[y] = 2，显然，dfn[] 是越来越大的，而 low 若没有返祖边也是越来越大的，所以就可以用这个条件为判断当前这个点是否为割点，即若 $low[y]\ge dfn[x]$ 并且 $x$ 不为根节点或 $x$ 为根节点且 $cnt>2$，就可以将 $x$ 标记为割点。

这个算法的正确性显而易见，这里就不过多的赘述了。

代码

void Tarjan(int x) { // 当前递归到了节点x
	dfn[x] = low[x] = ++t; // 更新
	int cnt = 0; // 统计有多少个儿子
	for (auto y : g[x])
		if (!dfn[y]) { // 树边
			cnt++; // 统计儿子
			Tarjan(y); // 展开子树
			low[x] = min(low[x], low[y]); // 更新low，这个不懂的先去看下我的另外一篇文章。
			if (dfn[x] <= low[y]) // 如果没有返祖边向上连
				if (root != x || cnt > 1) // 并且不能为根节点或者有两个子树以上
					flag[x] = true; // 标记
		} else low[x] = min(low[x], dfn[y]); // 返祖边
}

桥

题目

题目传送门

什么是桥

桥的定义：去掉这条边，会使连通块数量增加（只针对无向图）。

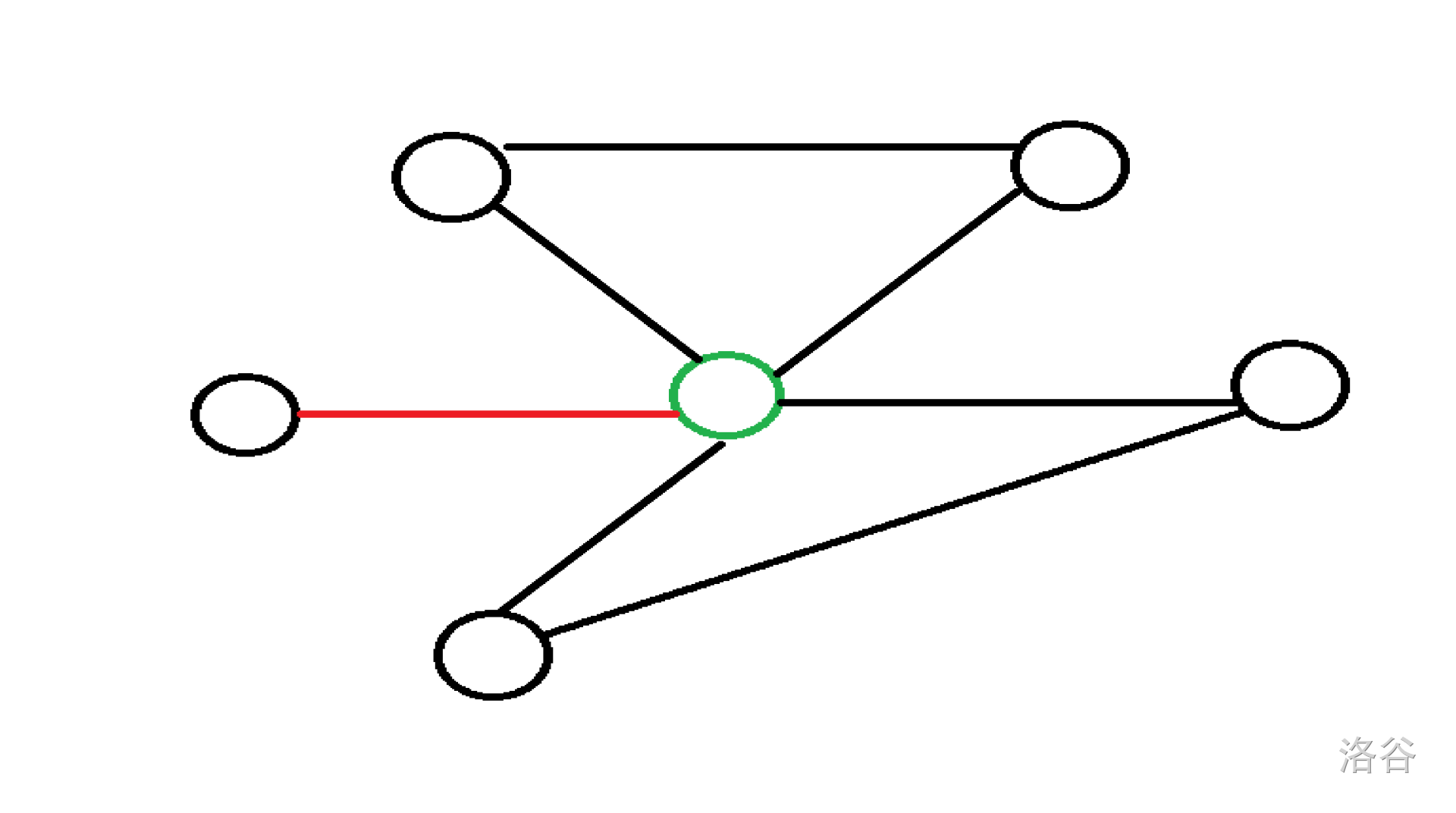
这个红色的边就是桥，因为删掉这条边可以让图变成两个部分，而其他的边都不是桥。

原理

与割点类似，$low$ 数组的含义也一样，只是再分析上有略微不同。

相同的内容就不在过多的赘述了，这里就讲不同点。
还是一样的图：

若 $x$ -> $y$，要是桥，就一定没有一条返祖边起点在 $x$ 下方，终点在 $y$ 的上方（在 $x$ 或者 $x$ 的上方），这也是与割点的最大的不同点，而且他不用判断当前是否为根节点，但是因为存双向边是存两个单向边，对判断桥是有影响的，所以在 tarjan 这个递归函数的参数还得多加一个参数 $id$，表示上次递归过的边的编号，如果这次还是遍历这条边，直接 continue 即可。

代码

Tarjan

void tarjan(int x, int id) {
	dfn[x] = low[x] = ++t;
	for (auto [y, wi] : g[x]) {
		if (id == wi) continue;
		if (!dfn[y]) {
			tarjan(y, wi);
			low[x] = min(low[x], low[y]);
			if (low[y] > dfn[x]) flag[wi] = true;
		} else low[x] = min(low[x], dfn[y]);
	}
}

主程建图

for (int i = 1; i <= m; i++) {
			int u, v;
			cin >> u >> v;
			g[u].push_back({v, i});
			g[v].push_back({u, i});
		}

完结撒花~~~~