论文阅读-地理感知顺序位置推荐

这是一篇发表在2020年KDD上的一篇文章，在本文中，作者提出了一种基于自注意力网络的地理感知序列推荐模型，其主要有以下三种特点：（1）提出了一个基于重要性采样的的损失函数，通过使用信息负样本来解决数据稀疏的问题。（2）提出了一个基于自注意力的地理编码器，来表示地理位置。（3）提出了具有地理感知的负样本，来提高负样本的信息性。

1.符号定义

用户的一条移动轨迹定义为：
$S^u=r_1^u\to r_2^u\to \cdots \to r_n^u$
其中，$r_i^u=\left(u,t_i,l_i,p_i\right)$代表用户在时间$t_i$访问某一经纬度的位置。

本文所研究的问题是根据当前轨迹信息预测下一个位置。

2. 模型结构

2.1 地理感知自注意力网络

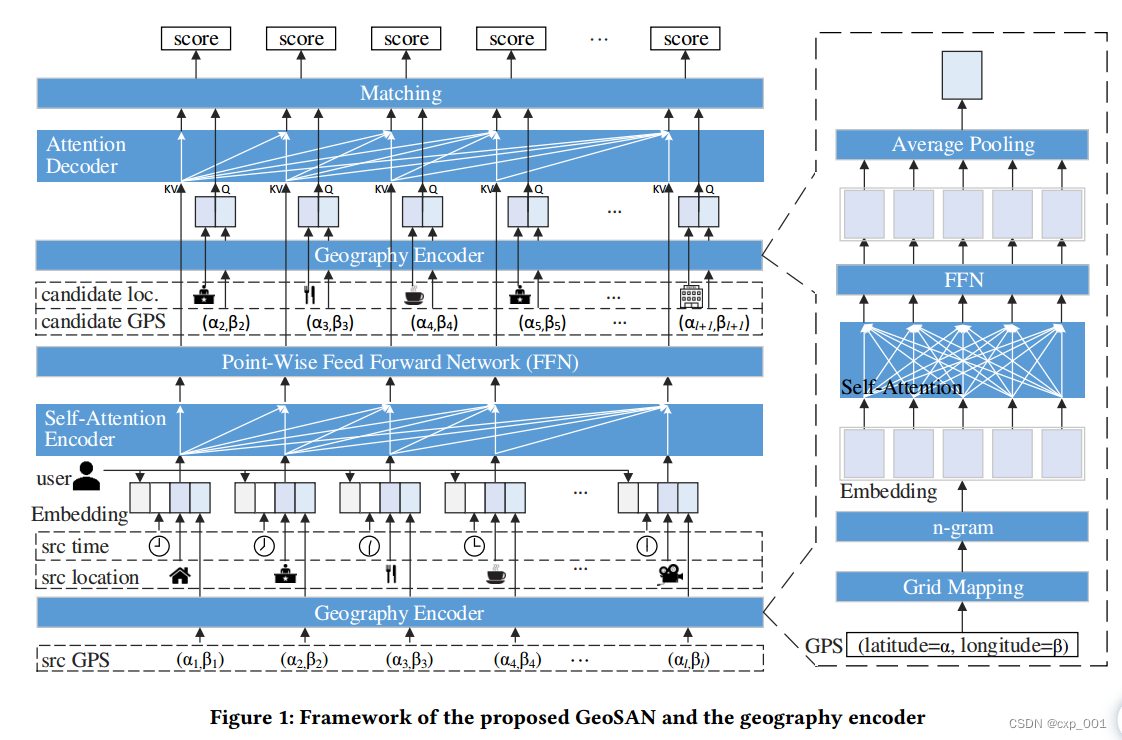
作者将轨迹划分为长度为m的序列，分别对序列中的user、hour、location信息进行嵌入，并使用地理编码器对精确地址(GPS)进行编码。然后将这些特征拼接，得到$\mathbf{E}\in {\mathbb{R}}^{m\times d}$.

然后作者使用自注意力来转换$E$，使用三个不同的矩阵$W_Q,W_K,W_V\in {\mathbb{R}}^{d\times d}$，
$$S=\mathrm{SA}(E)=\mathrm{attention}(E{W}_Q,E{W}_K,E{W}_V)(1)$$

2.1.1 注意力编码器

其中attention使用的是自注意点积注意力，

$$\mathrm{Atention}(Q,K,V)=\mathrm{softmax}(\frac{Q{K}^T}{\sqrt{d}})V(2)$$

最终s的维度是${\mathbb{R}}^{m\times d}$。
然后将s输入到前馈神经网络：

$$F_i=\mathrm{FFN}(S_i)=\max (0,S_i{W}_1+{\mathbf{b}}_1)W_2+{\mathbf{b}}_2(3)$$

其中，$W_1\in {\mathbb{R}}^{d\times d_h},W_2\in {\mathbb{R}}^{d_h\times d}$。
在堆叠多个自注意块时，在FFN和自注意层中使用残差连接和层归一化，以稳定和加速训练过程。

2.1.2 地理感知注意力解码器

为了改善输入序列相对于目标位置的表示，作者引入了目标感知注意力解码器，
$$A=\mathrm{decoder}(F^{(l)}|\mathbf{T})=\mathrm{Attempt}(\mathbf{T},{\mathbf{F}}^{(l)}W,{\mathbf{F}}^{(l)})(4)$$
其中，$T\in {\mathbb{R}}^{n\times d_T}$是输出序列的表示矩阵，由候选位置的嵌入向量与其地理信息的表示向量拼接而成。

W是一个矩阵，用于将查询和键映射到相同的潜在空间。

2.1.3 计算匹配函数

作者将输入序列$A_i$和候选位置$T_j$进行匹配，得到一个匹配分数，
$$y_{i,j}=f({\mathbf{A}}_i,{\mathbf{T}}_j),(5)$$
其中，$T_j$是候选位置$j$的表示向量。

2.2 地理编码器

为了捕捉地理位置之间的相互关系，作者提出了地理编码器来将位置的经纬度信息进行网格划分，然后使用自注意力网络来对网格的quadkey表示进行嵌入。

作者使用Tile Map System将地图投影到一个平面上，然后，每次将平面一分为4，再继续划分，最终平面的索引组成地理位置的quadkey。

然后，对包含经纬度信息的位置表示quadkey，作者对其进行了编码。如果直接对最后一层的quadkey直接进行编码会丧失位置之间的距离关系，作者将quadkey视为一个序列，然后对其进行n-gram划分，使用自注意力网络对序列进行编码，然后使用平均池化对来聚合n-gram表示的序列。

2.3 重要性采用损失函数

作者认为随着候选位置数量的增加，传统的交叉熵损失函数是无效的（？why），现阶段大部分使用二元交叉熵损失函数（和我理解的不太一样）：
$$-\sum _{S^u\in S}\sum _{i=1}^n\left(\log \sigma (y_{i,o_i})+\sum _{k\notin L^u}\log (1-\sigma (y_{i,k}))\right),(7)$$
其中，$L^u$是用户曾经到过的位置的集合，该公式每次都从用户未到过的地方采样一个负样本（不是可以采样k个吗）。

作者认为只采样一个负位置会导致数据利用不充分，因此应该多采几个。但是，如果以偏好得分前k个作为负样本是不可取的，因为它们可能是用户接下来要访问的位置；根据偏好得分计算概率进行采样也是不可行的，因为效率问题。

作者提出了建议对所有未访问过的位置进行加权，
$$-\sum _{S^u\in S}\sum _{i=1}^n\left(\log \sigma (y_{i,o_i})+\sum _{k\ne L^u}P(k|i)\log (1-\sigma (y_{i,k}))\right),(8)$$
其中，$P(k|i)$是所有负样本中偏好分数的概率：
$$P(k|i)=\frac{\exp (r_{i,k}/T)}{{\sum }_{k^{\prime }\notin L^u}\exp (r_{i,k^{\prime }}/T)}(9)$$
其中，$r_{i,k}$是第i步对位置k的偏好分数。
同样，在计算概率归一化的时候，仍然会存在之前提到的效率很低的问题。

作者使用非归一化概率$\begin{array}{r}\tilde{Q}(k|i)\end{array}$来代替原始的概率分布$Q(k|i)$，最终损失函数计算如下：
$$-\sum _{S^a\in S}\sum _{i=1}^n\left(\log \sigma (y_{i,o_i})+\sum _{k=1}^K{w}_k\log \left(1-\sigma (y_{i,k})\right)\right),(10)$$
(脑子懵懵的，不是很懂)
其中，$w_k=\frac{\exp \left(r_{i,k}/T-\ln \tilde{Q}(k|i)\right)}{{\sum }_{k^{\prime }=1}^K\exp \left(r_{i,k^{\prime }}/T-\ln \tilde{Q}(k^{\prime }|i)\right)}$。
在K个地点中，偏好分数越大的地点被赋予的权重越大。（why）

2.4 地理感知负采样器

作者认为位置中的地理信息也可以帮助区分未访问位置的消极性，例如当前访问位置的周围位置更有可能是消极的（？？？？）。作者建议在地理感知的负样本中，建议首先检索K个离目标位置最近的位置，然后从这K个候选点中随机抽取负样本。作者考虑了基于均匀分布和基于流行度分布的两种抽样方式。在基于流行度的抽样方式中，作者建议使用概率分布$\widetilde{Q(k|i)}\propto \text{ln}(c_k+1)$，其中，$c_k$是轨迹历史中出现的频率。

模型的结构图放上来：

3.实验

3.1 数据集

作者使用了三个真实世界的数据集，: Gowalla, Brightkite,
Foursquare

对于每个用户的签入序列，作者使用以前未访问过的位置的最后一个签入记录进行评估，并在此之前的所有签到序列进行培训。

3.2 baseline

（1）PRME-G：度量学习
（2）FPMC-LR：因式分解
（3）GRU
（4）SASRec：使用自注意力机制
（5）STGN：使用时空门增强LSTM网络

3.3 metrics

命中率和NDCG

3.4 result

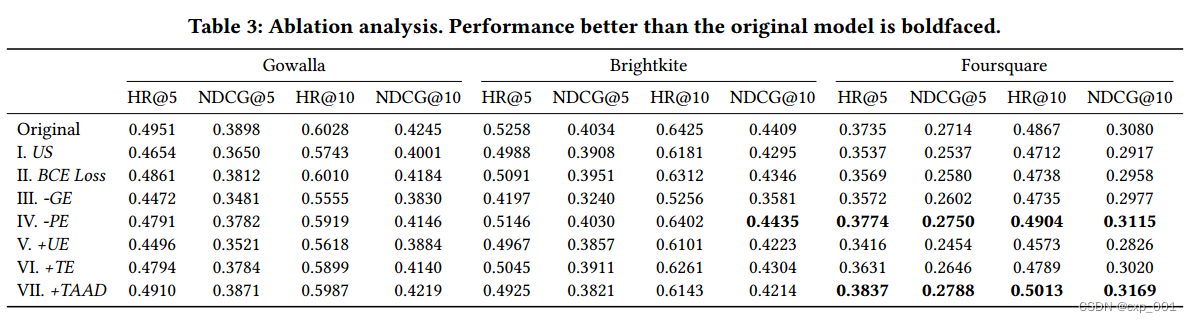
3.5 消融实验

作者考虑了以下几个模型的变体：
（1）US（Uniform Sampler）:在所有位置使用统一负采样器。
（2）BCE(二元交叉熵)损失:使用二元交叉熵损失，不给负样本分配权重。
（3）Remove GE (Geography Encoder)：移除地理编码器，只使用位置嵌入来表示。
（4）Remove PE (Positional Embedding) in GE:去掉了地理编码器中使用的位置嵌入，它会在一个quadkey中注入每个n-gram token的相对位置信息。（不懂）
（5）Add UE (User Embedding): 将用户嵌入添加到签入序列编码器。
（6）Add TE (Time Embedding):添加一个时间嵌入。
（7）Add TAAD (Target-Aware Attention Decoder):添加了目标感知注意力解码器。

最终结果：

4.结论

简单来说，本文作者提出了一个新的模型来实现下一个位置的推荐，主要贡献课总结为三点：（1）提出了一种新的基于重要性抽样的损失函数，可以更好地利用信息性负样本。（2）提出了一种新的地理编码器来融合地理信息。（3）提出了地理感知的负向采样器，以提高样本负向位置的信息量。

论文链接：paper