OpenCV(四十三)：分水岭法

什么是分水岭算法？

分水岭算法（Watershed Algorithm）是一种经典的基于数学形态学的图像分割方法，常用于解决相互接触或重叠目标的分割问题，在医学图像、显微镜图像、工业检测等领域应用广泛。

“分水岭”这一名称来源于地理学中的概念：
将灰度图像看作一幅地形图（Topographic Surface）：

• 像素灰度值 → 地形高度
• 灰度低的区域 → 山谷（盆地）
• 灰度高的区域 → 山峰（分水岭）

通过模拟从低洼处“注水”的过程，当不同盆地的水即将汇合时，建立“堤坝”，这些堤坝即构成分割边界。

分水岭算法的基本思想

1. 地形模型

给定一幅灰度图像 I(x,y)，将其视为一个三维地形：

• (x,y)：空间位置
• I(x,y)：高度值

算法从局部最小值（Local Minima）开始注水，每一个最小值对应一个初始区域。

2. 注水与合并过程

分水岭的核心过程可以描述为：

1. 从所有局部极小值开始“注水”
2. 水位逐渐升高
3. 相邻区域的水即将接触时，构建分水岭边界
4. 最终形成多个互不连通的区域

如果不加限制，分水岭算法会产生大量细碎区域（过分割），这是其最大缺点。

数学与形态学基础

1. 极小值与集水盆（Catchment Basin）

• 集水盆：所有最终流向同一极小值的像素集合
• 分水岭线：不同集水盆之间的边界像素集合

形式化定义中，分割结果可以表示为：

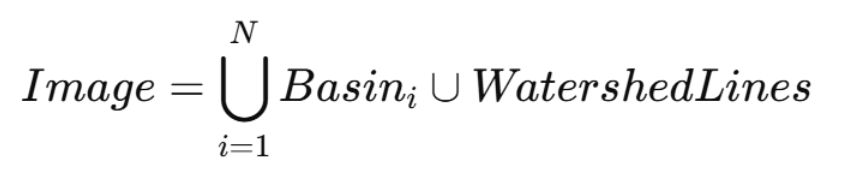
2. 梯度图的重要性

在实际应用中，分水岭通常不直接作用于原始图像，而是作用于梯度图像：

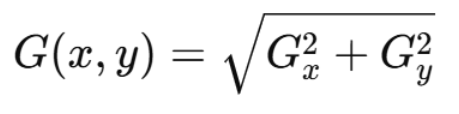
原因是：

• 区域内部梯度小
• 区域边界梯度大
• 更容易在边界处形成分水岭

OpenCV 中常用 Sobel 或 Laplacian 计算梯度。

过分割问题与标记控制分水岭

1. 过分割现象

由于噪声、纹理和微小灰度变化，分水岭会产生大量局部极小值，导致：

• 目标被切割成许多小块
• 分割结果难以使用

2. 标记控制分水岭（Marker-based Watershed）

为解决过分割问题，OpenCV 实际使用的是标记控制分水岭算法，核心思想是：

人为指定“可靠的前景”和“可靠的背景”，限制分水岭的生长范围

标记图（Markers）中：

• 不同整数 → 不同区域
• 0 → 未知区域
• -1 → 分水岭边界（OpenCV 输出）

示例

分水岭算法整体流程：

1. 读取图像
2. 灰度化
3. 二值化（阈值或 Otsu）
4. 形态学去噪
5. 距离变换（Distance Transform）
6. 确定前景 markers
7. 确定背景 markers
8. 构造 marker 图
9. 调用 cv2.watershed()
10. 可视化分割结果

import cv2
import numpy as np
import matplotlib.pyplot as plt

def watershed_demo(image_path):
    # 1. 读取图像
    img = cv2.imread(image_path)
    if img is None:
        raise ValueError("图像读取失败，请检查路径")

    img_show = img.copy()
    img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

    # 2. 灰度化
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

    # 3. 二值化（Otsu + 反色）
    ret, binary = cv2.threshold(
        gray, 0, 255,
        cv2.THRESH_BINARY_INV + cv2.THRESH_OTSU
    )

    # 4. 形态学开运算（去噪）
    kernel = np.ones((3, 3), np.uint8)
    opening = cv2.morphologyEx(
        binary, cv2.MORPH_OPEN, kernel, iterations=2
    )

    # 5. 膨胀，确定“确定背景”
    sure_bg = cv2.dilate(opening, kernel, iterations=3)

    # 6. 距离变换，确定“确定前景”
    dist_transform = cv2.distanceTransform(opening, cv2.DIST_L2, 5)
    ret, sure_fg = cv2.threshold(
        dist_transform,
        0.7 * dist_transform.max(),
        255,
        0
    )
    sure_fg = np.uint8(sure_fg)

    # 7. 未知区域
    unknown = cv2.subtract(sure_bg, sure_fg)

    # 8. 连通域标记
    ret, markers = cv2.connectedComponents(sure_fg)

    # markers + 1，保证背景不是 0
    markers = markers + 1

    # 未知区域标记为 0
    markers[unknown == 255] = 0

    # 9. 分水岭算法
    markers = cv2.watershed(img, markers)

    # 10. 可视化分水岭边界（-1）
    img_show[markers == -1] = [0, 0, 255]  # 红色边界

    # 11. 显示结果
    titles = [
        "Original",
        "Binary",
        "Opening",
        "Sure Background",
        "Sure Foreground",
        "Watershed Result"
    ]
    images = [
        img_rgb,
        binary,
        opening,
        sure_bg,
        sure_fg,
        cv2.cvtColor(img_show, cv2.COLOR_BGR2RGB)
    ]

    plt.figure(figsize=(12, 8))
    for i in range(len(images)):
        plt.subplot(2, 3, i + 1)
        plt.imshow(images[i], cmap='gray')
        plt.title(titles[i])
        plt.axis('off')
    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    # 示例图片路径（如 coins.png、cells.png）
    watershed_demo("coins.png")

执行结果：

总结

OpenCV 分水岭算法本质上是一种：

基于拓扑地形和数学形态学的区域分割方法

通过引入标记控制机制，分水岭从理论方法转变为工程可用算法。
在实际项目中，它常与阈值分割、距离变换、形态学处理联合使用，是解决粘连目标分割问题的经典方案。