论文理解【RL - Exp Replay】—— 【DisCor】Corrective Feedback in RL via Distribution Correction

• 标题：DisCor: Corrective Feedback in Reinforcement Learning via Distribution Correction
• 文章链接：DisCor: Corrective Feedback in Reinforcement Learning via Distribution Correction
• 作者博客：Does On-Policy Data Collection Fix Errors in Off-Policy Reinforcement Learning?
• 发表：NIPS 2020
• 领域：强化学习 —— Experience Replay

---

• 摘要：Deep RL 可以学习各种任务的有效策略，但由于不稳定性和对超参数的敏感性难以使用，其原因尚不清楚。在本文中，我们研究了基于 Bootstrap Q-learning 的 RL 方法如何因 “函数近似” 和 “用于训练Q函数的数据分布” 之间的病态相互作用受到损害：在标准监督学习中，on-line 数据收集应引起纠正反馈，新收集的数据会纠正旧预测中的错误。而使用 Q-Learning 等动态编程方法时可能没有此类反馈，这可能导致潜在的不稳定性，次优收敛性，以及在从嘈杂，稀疏或延迟的奖励中学习时性能不佳。基于这些观察结果，我们提出了一种新算法 Discor，该算法显式地优化了可以校正值函数中累积错误的数据分布。Discor 计算出一个可以最好地纠正 Q 价值估计误差的纠正性采样数据分布的可行近似值，其结果指导我们根据 Q 价值估计的准确性重新加权样本进行训练。实验表明，Discor 在一系列具有挑战性的 RL 设置中实现了大量提升，例如多任务学习和从嘈杂的奖励信号中学习
  

1. 背景

• 本文方法是针对价值学习设计的，目标是减少学习 $Q^{\ast }$ 时的误差。对于不学习价值估计器的方法（比如使用 MC return 的方法）不适用
• 作者 idea 的核心是 “（需要估计价值的）强化学习通常使用的近似动态规划方法（ADP）中，缺少监督学习中常见的纠正性反馈”，我们首先对此进行说明

1.1 强化学习的特点

• 先看一下 RL 和普通 SL 的几个区别，这里每一个点都可以引出很多 RL 独有的问题和挑战，本文关注的问题主要是由于后两点导致的
  1. Balance between exploration and exploitation
  2. Agent’s action affect the subsequent data it received (action affects the environment)
  3. Delayed reward
  4. Time matters (sequential data, not i.i.d)

1.2 近似动态规划算法（Approximate Dynamic Programming, ADP）

• 一句话说，ADP 就是使用函数近似法，基于 Bellman operator 或 Bellman optimal operator 进行价值估计的方法，也就是摘要中所谓的 “基于 Bootstrap Q-learning 的 RL 方法”

• 以估计 $Q^{\ast }$ 为例

  1. 动态规划 DP 方法反复迭代以下等式直到价值收敛，这是我们初学 RL 时在 model-based 那块就接触过的
     $$Q\left(S_t,A_t\right)\leftarrow Q\left(S_t,A_t\right)+\alpha \left[R_{t+1}+\gamma \underset{a}{\max }Q\left(S_{t+1},a\right)-Q\left(S_t,A_t\right)\right]$$
  2. 近似动态规划 ADP 引入了一个函数估计器来代替 DP 中的价值表格，并通过优化基于 TD error 的损失函数来优化这个估计器。比如 DQN 就是引入了一个价值网络
     $$\theta \leftarrow \arg \underset{\theta }{\min }{\mathbb{E}}_{s,a\sim \mathcal{D}}\left[{\left(Q_{\theta }(s,a)-\left(r(s,a)+\gamma {\mathbb{E}}_{s^{\prime }\mid s,a}\left[\underset{a^{\prime }}{\max }\bar{Q}\left(s^{\prime },a^{\prime }\right)\right]\right)\right)}^2\right]$$

  注意，无论是 DP 还是 ADP，本质都是基于时序差分方法 TD 的，终极目标是让所有 $(s,a)$ 处的价值估计尽量靠近 TD target

• 为了便于后续分析，这里先说明 TD 方法和函数近似方法的特点

  1. TD 本质是一种以匹配 Bellman equation 或 Bellman optimal equation 为目标的非平稳增量式 MC 方法。因此某个 $(s,a)$ 处进行的更新越多，该位置及其相邻 $(s,a)$ 之间的 Q 价值估计越符合 Bellman equation 或 Bellman optimal equation。相关公式分析可以参考 强化学习拾遗 —— 强化学习的样本效率 2.1.3 节
  2. 函数近似方法本质是一种利用先验知识，通过计算优化少量参数来估计大量参数的方法，我们利用先验知识设计估计器的结构（线性回归、决策树、随机森林、神经网络…），然后优化它来拟合少数位置的数据，最后利用其泛化性来得到所有位置的估计值。这种情况下，显然在哪里算得多哪里就拟合得更准确，越利用泛化性得到估计值就越不准确；另一方面由于泛化性的存在，在某个位置计算更新时，与该位置有相似特征的位置的估计值也会变化，而且这种附带的变化可能是有害的

1.3 纠正性反馈（Corrective Feedback）

• 在监督学习中数据服从 i.i.d 分布，我们认为样本标记都是从真实的目标分布中直接采样出来的。学习过程中的任意一次更新，都是在让估计器更加靠近这个 ground truth 分布。换句话说，一旦估计器偏离真实分布，那么下一个样本学习时就能对他进行纠正，使得估计越来越靠近 ground truth，这就是所谓的 纠正性反馈

• 从强化学习的视角来看，上下文赌博机（context bandit）是一种具有纠正性反馈的类 RL 设置，在这个情景（或环境）中，agent 面对数台不同的赌博机，每一台都有多个摇臂，每个摇臂对应一个 reward 分布，拉动即可获得即时 reward。赌博机、上下文赌博机都是早期 RL 研究的重点，它们和完整 RL 设置的主要区别如下
  
  对于赌博机环境的详细说明请参考 强化学习笔记（2）—— 多臂赌博机，对于上下文赌博机而言，其有一个重要特点是 “某个 $(s,a)$ 位置的即时奖励，仅和此 $(s,a)$ 位置的价值估计相关”，因此就像监督学习那样，每个 transition 样本的 “标签”（即时reward）可以看做从一个 $Q^{\ast }(s,a)$ 的 ground truth 中 i.i.d 采样得到的，这时损失为
  $$\mathcal{L}(Q)={\mathbb{E}}_{s\sim \beta (s),a\sim {\pi }_k(a\mid s)}\left[\left|Q_k(s,a)-Q^{\ast }(s,a)\right|\right]$$ “纠正性反馈” 在这种 RL 设定的情形下的体现如下，可见这时对任意交互动作的学习，都能针对性地纠正价值估计的偏差

  1. Some state value over-estimated
  2. Policy chooses action correspond to it
  3. Observes the corresponding $r(s,a)$, or $Q^{\ast }(s,a)$
  4. Minimize $\mathcal{L}(Q)$, which correct the Q-values precisely

• 总之，纠正性反馈使得数据收集过程和误差矫正过程之间可以建设性地交互（constructive interaction），使得价值估计快速且稳定地收敛

2. 本文方法

2.1 思想

2.1.1 RL 缺乏纠正性反馈 ADP

• 作者认为 RL 方法中缺乏纠正性反馈 ADP，对比一下 1.3 节中上下文赌博机和常见 DRL 方法的损失
  $$\begin{array}{rl}\text{Context bandit}:& \mathcal{L}(Q)={\mathbb{E}}_{s\sim \beta (s),a\sim {\pi }_k(a\mid s)}\left[\left|Q_k(s,a)-Q^{\ast }(s,a)\right|\right]\\ \text{RL}:& \mathcal{L}(Q)={\mathbb{E}}_{s\sim \beta (s),a\sim {\pi }_k(a\mid s)}\left[\left|Q_k(s,a)-{\mathcal{B}}^{\ast }{Q}_k(s,a)\right|\right]\end{array}$$ 可见对于上下文赌博机，其优化目标 $Q^{\ast }$ 一定是准确的（即是采样自 ground truth 的）；而在一般的 RL 设定中，其优化目标 TD target 可能不准确

  • 如果深究 TD target 不准确的原因，这和 1.1 节中提到的强化学习的后两个特点有关。由于无法获取即时反馈，一个 transition 准确的标记（即 return）必须等待该 episode 终止才能获得，这样做（MC方法）的效率太低了，有时甚至无法实现（没法得到完整轨迹）。TD 是这种情况下不得不使用的折衷方法，它使用 bootstrap 技巧，基于当前的估计构造优化目标，虽然这样可以得到即时标记（TD target），但它是基于当前估计的，而且学习这个估计使用的样本标记不是来自 ground truth 的 i.i.d 采样，这样就出现了偏差，纠正性也就不存在了。一般 RL 的设定下，agent 执行一个 $(s,a)$ 不但影响即时 reward，而且也会影响下一个时刻的 reward 和状态，任意一个 $(s,a)$ 的 reward 不仅和自身的 $Q$ 价值绑定，还会影响其他状态的价值估计，这就导致最终的价值估计和策略有关，而学习过程中的策略又是非平稳的，学习样本不可能来自 ${\pi }^{\ast }$，因此价值估计时使用的样本也不可能是来自 $Q^{\ast }$ 的 i.i.d 采样
  • 给出一个更加直观的例子：agent 从左上角出发，上下左右运动，仅在右下角位置可以获得 25 的 reward，使用 $ϵ$ 衰减的 $ϵ$-greedy 探索策略，Q-learning 方法，价值收敛过程如下。可见很多位置颜色忽明忽暗，价值收敛过程中出现过很多震荡，这也能说明 TD target 是渐进准确的
    

  如果优化目标不准确，每一步的价值更新就会缺乏纠正性，最终收敛的价值也会不准确

• 当引入函数近似时，上述问题会更加严重，回顾下 1.2 中说明的函数近似方法的两个特点 “计算越多的位置越准确” 和 “有相似特征的位置会受到泛化性影响”，看以下示例
  
  这是一个有 7 个状态的树状 MDP，agent 从根状态出发（最上面）向叶子状态（最下面）移动。其中形状一样的状态有相似的特征，每张图的虚线框表明了该轮更新时使用的交互轨迹（on-policy 设定），状态颜色越绿说明其价值估计越准确，越红则越不准确。从图中可以发现优化过程出现多次震荡（由于当前轨迹更新时使用不准确的 TD target 以及对相似状态状态的泛化性，打圈部分原本估计较好的状态估计又变坏了），仔细来看有以下三点

  1. 叶子状态：访问（采样计算）较少，Bellman optimal equation 符合性较差，（使用函数近似时）拟合较差，由于在轨迹尾部，这会提供有较大误差的 TD target
  2. 根状态：访问（采样计算）较多，Bellman optimal equation 符合性较好，（使用函数近似时）拟合较好，学到了误差很大的 TD target
  3. 使用函数近似时，具有相似特征的状态在更新时互相影响（有可能原本在叶子处一个误差较小的状态，受到根部状态更新时的泛化影响后误差变大了，进而其提供的 TD target 也变差了）

  这个例子很好地说明了 RL 中缺乏纠正性反馈的表现和本质原因

2.1.2 缺乏纠正性反馈 ADP 导致的问题

• 先定义一个 value error 的概念，它是当前价值估计相对最优 $Q^{\ast }$ 的差距关于当前策略下 $(s,a)$ 分布 $d_k^{\pi }$ 的期望，即
  $${\mathcal{E}}_k:={\mathbb{E}}_{d_k^{\pi }}[|Q_k-Q^{\ast }|]$$

  1. 如果学习过程中 ${\mathcal{E}}_k$ 没有平稳地减小，说明学习过程中经常缺失纠正性反馈；
  2. 如果 ${\mathcal{E}}_k$ 最终稳定在非零位置，说明价值估计过早收敛

• 作者在一个 grid world MDP 环境中进行了实验，并绘制了 $d_k^{\pi }$ 和 ADP 更新前后 Bellman error $|Q_{k+1}-{\mathcal{B}}^{\ast }{Q}_k|(s,a)$ 及 value error difference ${\mathcal{E}}_{k+1}(s,a)-{\mathcal{E}}_k(s,a)$ 的相关性，实验中每轮更新都使用了 MDP 的所有 transition（按 $d_k^{\pi }$ 加权）从而消除采样误差，结果如下
  

  1. 虚线说明：无论训练的什么阶段，某个 $(s,a)$ 访问频率越高，越符合 Bellman optimal equation
  2. 实线说明：训练过程早期，由于 TD target 不准，$(s,a)$ 访问频率越高，其价值估计和 $Q^{\ast }$ 的偏差越大；随着训练进行 TD target 会逐渐准确，很多 (s,a) 的 TD target 变准确了，这个正相关性逐渐下降，直到最终收敛时二者不再具有相关性。我们可以简单地总结为：某个 $(s,a)$ 访问频率越高，其价值估计和 $Q^{\ast }$ 的偏差越大

• 作者进一步对 on-policy、off-policy+replay buffer、均匀采样等设定进行了实验，说明了缺乏纠正性反馈导致的三大问题
  

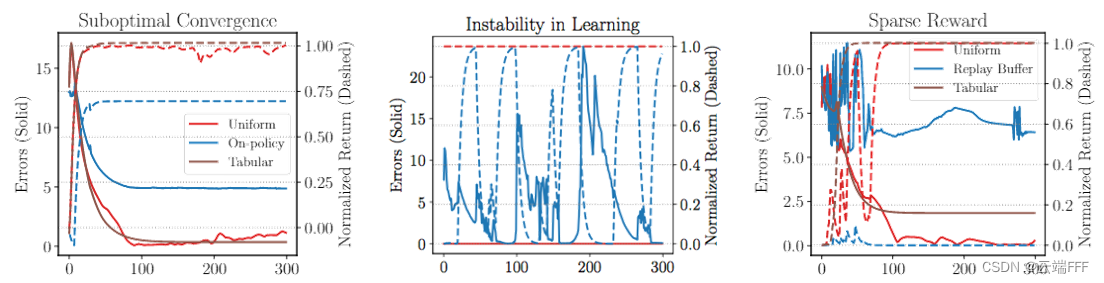
  1. 次优收敛：看最左边图蓝色线，${\mathcal{E}}_k$ 最初快速下降，最终收敛到一个明显大于0的值，说明在没有采样误差的情况下，on-policy 采样也会导致ADP收敛到一个次优解。另外当使用均匀采样（相当于增加2.1.1节叶状态计算概率；减少根状态计算概率）或使用表格型方法（不做函数近似，回避了泛化和估计器误差）时会改善
  2. 学习过程不稳定：看中间图蓝色线（off-policy + replay buffer 设定），我们观察到即使最新策略获得的回报非常接近最佳回报（红色线），算法也容易退化
  3. 当信噪比太高时（奖励稀疏时）无法学习：看右图蓝色虚线，可见稀疏奖励时学习无法进行，这里给 agent 提供了所有 transition 进行学习，因此并不是探索问题。另外当使用均匀采样（相当于增加2.1.1节叶状态计算概率；减少根状态计算概率）或使用表格型方法（不做函数近似，回避了泛化和估计器误差）时会改善

2.1.3 作者的思路

• 回头看 1.2 节中 ADP 的更新公式
  $$\theta \leftarrow \arg \underset{\theta }{\min }{\mathbb{E}}_{s,a\sim \mathcal{D}}\left[{\left(Q_{\theta }(s,a)-\left(r(s,a)+\gamma {\mathbb{E}}_{s^{\prime }\mid s,a}\left[\underset{a^{\prime }}{\max }\bar{Q}\left(s^{\prime },a^{\prime }\right)\right]\right)\right)}^2\right]$$ 注意其中 $(s,a)$ 是从一个分布 $\mathcal{D}$ 中采样出来的

  1. 对于 on-policy 方法而言 $\mathcal{D}$ 是当前策略诱导的 $(s,a)$ 的边际分布$${\mathcal{D}}_k(s,a)=d^{\pi }(s,a)=d^{\pi }(s)\pi (a|s)=\sum _{t=0}^{\infty }{\gamma }^{t}p(S_t=s|\pi )\pi (a|s)$$
  2. 对于 off-policy 方法而言 $\mathcal{D}$ 是构成 replay buffer 的过往策略的混合 $${\mathcal{D}}_k=\frac{1}{k}\sum _{i=1}^k{d}^{{\pi }_i}$$

  根据前文分析，无论哪种情况下都会缺失纠正性反馈，因此作者的想法是优化一个最好的采样分布 $\mathcal{D}$，按它进行采样学习可以最好地纠正当前价值估计的偏差，从而使最后收敛的价值尽量靠近真实 $Q^{\ast }$。

• 不妨把第 $k$ 轮迭代时优化得到的最佳分布表示为 $p_k$，把此时 replay buffer 中的混合数据分布表示为 ${\mu }_k$，直接把 $\frac{p_k}{{\mu }_k}$ 作为重要性采样比对损失函数重加权，即
  $$Q_k\leftarrow \arg \underset{Q}{\min }\frac{1}{N}\sum _{i=1}^N{w}_i(s,a)\cdot {\left(Q(s,a)-\left[r(s,a)+\gamma Q_{k-1}\left(s^{\prime },a^{\prime }\right)\right]\right)}^2$$ 示意图如下
  

• 可以看到这篇文章最后做的还是一个非均匀经验回放的事情，我前面也分享过几篇关于这个的文章，比如 PER、PAL/LAP 等，不过该文章和他们的一个重要区别是

  1. 那些文章都默认均匀重放时的收敛结果是好的，所以保持非均匀重放后损失的期望梯度不变，试图在增加收敛速度的同时保持收敛结果尽量不变
  2. 本文认为由于 ADP 缺乏纠正性反馈，均匀重放时的收敛结果不好，因此在重加权时没有考虑保持期望梯度

• 最后再举个例子，对于 2.1.1 节的树状 MDP，一个较好的更新优先级可能是先关注叶子部分，再逐层向上，从而保证 TD target 始终比较准确，即
  

2.2 计算最优纠正分布

2.2.1 符号说明

1. MDP：$(\mathcal{S},\mathcal{A},P,R,\gamma ,{\rho }_0)$
2. 策略 $\pi$ 的边际状态折扣分布：$d^{\pi }(s)={\sum }_{t=0}^{\infty }{\gamma }^{t}p(S_t=s|\pi )$
3. 策略 $\pi$ 的边际状态动作折扣分布：$d^{\pi }(s,a)=d^{\pi }(s)\pi (a|s)$
4. 策略 $\pi$ 的状态动作转移矩阵 $P^{\pi }$（这是个 $(|\mathcal{S}|\times |\mathcal{A}|)\times (|\mathcal{S}|\times |\mathcal{A}|)$ 的矩阵）：$$P^{\pi }Q(s,a):={\mathbb{E}}_{s^{\prime }\sim P(\cdot |s,a),a^{\prime }\sim \pi (a|s)}[Q(s^{\prime },a^{\prime })]$$

   Note: Bellman quation: $Q(s,a)={\mathbb{E}}_{s^{\prime }\sim P(\cdot |s,a),a^{\prime }\sim \pi (a|s)}[r(s,a)+\gamma Q(s^{\prime },a^{\prime })]$

5. Bellman optimal operator ${\mathcal{B}}^{\ast }$：$({\mathcal{B}}^{\ast }Q)(s,a)=r(s,a)+\gamma {\mathbb{E}}_{s^{\prime }|s,a}[{\max }_{a^{\prime }}\bar{Q}(s^{\prime },a^{\prime })]$
6. 策略诱导的状态动作分布 $\mu$
   1. 对于 on-policy 方法而言 $\mu$ 是 $(s,a)$ 的边际分布，${\mu }_k=d^{{\pi }_k}$
   2. 对于 off-policy 方法而言 $\mu$ 是构成 replay buffer 的过往策略的混合，${\mu }_k=\frac{1}{k}{\sum }_{i=1}^k{d}^{{\pi }_i}$
7. 函数近似的本质是对把 ${\mathcal{B}}^{\ast }$ 的结果投影到 $Q$ 函数空间 $\mathcal{Q}$ 上，使得 $Q_{k+1}\leftarrow {\Pi }_{\mu }({\mathcal{B}}^{\ast }Q)$，其中投影函数 $\Pi$ 定义为
   $${\Pi }_{\mu }(Q)\stackrel{\text{ def }}{=}\arg \underset{Q^{\prime }\in \mathcal{Q}}{\min }{\mathbb{E}}_{s,a\sim \mu }\left[{\left(Q^{\prime }(s,a)-Q(s,a)\right)}^2\right].$$

2.2.2 计算最优纠正分布

• 我们希望优化每一轮迭代中使用的 $(s,a)$ 分布能使每一轮的 ${\mathcal{E}}_k$ 最小化，得到以下优化目标
  $$\begin{array}{rl}& \underset{p_k}{\min }{\mathbb{E}}_{d^{{\pi }_k}}\left[\left|Q_k-Q^{\ast }\right|\right]\\ & \text{ s.t. }{Q}_k=\arg \underset{Q}{\min }{\mathbb{E}}_{p_k}\left[{\left(Q-{\mathcal{B}}^{\ast }{Q}_{k-1}\right)}^2\right],\sum _{s,a}{p}_k(s,a)=1,\forall s,a{p}_k(s,a)\ge 0\end{array}$$ 这个优化问题的解是
  $$p_k(s,a)\propto \exp \left(-\left|Q_k-Q^{\ast }\right|(s,a)\right)\frac{\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|(s,a)}{{\lambda }^{\ast }}$$ 其中 ${\gamma }^{\ast }\in {\mathbb{R}}^{+}$ 是优化问题中约束项 ${\sum }_{s,a}{p}_k(s,a)=1$ 的拉格朗日乘子的值，证明请参考第 5 节

• 在做 re-weight 的时候，简单地对 replay-buffer 中的数据分布应用重要度采样比 $w_k=p_k(s,a)/\mu (s,a)$ 有两个问题

  1. 高方差，学习不稳定
  2. replay buffer 中数据采样自的混合分布 $\mu (s,a)$ 不好估计

  这里第 2 点尤其棘手，因此作者选择将 $\mu$ 重加权到 $p_k$ 的一个投影 $q_k$ $$q_k=\arg \underset{q}{\min }-{\mathbb{E}}_{q(s,a)}[\log p_k(s,a)]+\tau D_{KL}(q(s,a)||\mu (s,a))$$ 其中 $\tau >0$ 是一个常数。这个式子就是说我们希望 $q_k$ 既要和 $p_k$ 靠近又要和 $\mu$ 靠近，使用 $\tau$ 来控制二者比例

  注：原文中这里没有一开始的负号，但那就意味着 $q_k$ 要远离 $p_k$，没有道理。这里也希望能和大家讨论

  下面我们来解 $q_k$，令梯度为 0，有
  $$\begin{array}{rl}\frac{\partial -q_k\log p_k+\tau q_k\log \frac{q_k}{{\mu }_k}}{\partial q_k}& =-\log p_k+\tau (\log \frac{q_k}{{\mu }_k}+\frac{{\mu }_k}{q_k}\frac{1}{{\mu }_k}{q}_k)\\ & =-\log p_k+\tau (\log \frac{q_k}{{\mu }_k}+1)\\ & \stackrel{令}{=}0\\ \Rightarrow \log \frac{q_k^{\ast }}{{\mu }_k}+1& =\frac{\log p_k}{\tau }\\ \Rightarrow e\frac{q_k^{\ast }}{{\mu }_k}& =\exp (\frac{\log p_k}{\tau })\\ \Rightarrow q_k^{\ast }& \propto {\mu }_k\cdot \exp (\frac{\log p_k}{\tau })\\ \Rightarrow \frac{q_k^{\ast }}{{\mu }_k}& \propto \exp (\frac{\log p_k}{\tau })\end{array}$$ 于是得到
  $$\frac{q_k^{\ast }}{{\mu }_k}\propto \exp \left(\frac{-\left|Q_k-Q^{\ast }\right|(s,a)}{\tau }\right)\frac{\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|(s,a)}{{\lambda }^{\ast }}$$ 这样就回避掉 $\mu$ 的计算了

• 注意上面 $Q^{\ast }$ 和 $Q_k$ 都是直接得不到的（$Q_k$ 是这一轮更新后得到的，而我们更新做重加权时就要用到 $Q_k$）。所以要考虑如何做替代，因为估计不准，所以替代时的核心思想是做 “降权”，即替代后得到的 $p_k$ 要小于公式表示的真实 $p_k$。具体而言，$\left|Q_k-Q^{\ast }\right|$ 要用其 upper bound 代替 ；$\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|$ 要用其 lower bound 代替

  1. 找 $|Q_k-Q^{\ast }|$ 的上界：

     • 设训练历史中折扣并传递的 Bellman 误差的累计总和为 ${\Delta }_k$，
       $$\begin{array}{rl}& {\Delta }_k=\sum _{i=1}^k{\gamma }^{k-i}\left(\prod _{j=i}^{k-1}{P}^{{\pi }_j}\right)\left|Q_i-\left({\mathcal{B}}^{\ast }{Q}_{i-1}\right)\right|.\text{ (vector-matrix form of }\Delta \text{ ) }\\ ⟹& {\Delta }_k(s,a)=\left|Q_k(s,a)-\left({\mathcal{B}}^{\ast }{Q}_{k-1}\right)(s,a)\right|+\gamma \left(P^{{\pi }_{k-1}}{\Delta }_{k-1}\right)(s,a).\end{array}$$ 其中 $P^{{\pi }_j}$ 是 ${\pi }_j$ 下的状态动作转移矩阵

     • Theorem 4.2 存在 $k_0\in \mathbb{N}$ 使得 $\forall k>k_0$ 有 ${\Delta }_k$ 满足以下不等式，且对于每个 $(s,a)$，随着 ${\pi }_k\to {\pi }^{\ast }$ 有 ${\Delta }_k\to |Q_k-Q^{\ast }|$
       $${\Delta }_k(s,a)+\sum _{i=1}^k{\gamma }^{k-i}{\alpha }_i\ge \left|Q_k-Q^{\ast }\right|(s,a),{\alpha }_i=\frac{2R_{\max }}{1-\gamma }\underset{s}{\max }{\mathrm{D}}_{\mathrm{TV}}\left({\pi }_i(\cdot \mid s),{\pi }^{\ast }(\cdot \mid s)\right)$$ 这样我们可以用 ${\Delta }_k+{\sum }_{i=1}^k{\gamma }^{k-i}{\alpha }_i$ 作为 $|Q_k-Q^{\ast }|$ 的上界。Theorem 4.2的证明请参考原文

  2. 找 $\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|$ 的下界：

     • 使用上一轮迭代中 $\left|Q_{k-1}-{\mathcal{B}}^{\ast }{Q}_{k-2}\right|$ 的最大和最小值来 bound 住，即认为
       $$\begin{gathered} \forall s,a{c}_1\le \left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|(s,a)\le c_2 \\ where{c}_1=\underset{s,a}{\min }\left|Q_{k-1}-{\mathcal{B}}^{\ast }{Q}_{k-2}\right|,c_2=\underset{s,a}{\max }\left|Q_{k-1}-{\mathcal{B}}^{\ast }{Q}_{k-2}\right| \end{gathered}$$
     • 回去看下上面，${\Delta }_k(s,a)$ 的计算中有 $\left|Q_k(s,a)-\left({\mathcal{B}}^{\ast }{Q}_{k-1}\right)(s,a)\right|$，那边要求上界，所以用 $c_2$ 代替

  把上述讨论全部结合起来

  1. 对于指数部分，用 ${\Delta }_k$ 作为 $|Q_k-Q^{\ast }|$ 的上界进行替代
  2. 在计算 ${\Delta }_k$ 时需要用到 $\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|$，用 $\left|Q_{k-1}-{\mathcal{B}}^{\ast }{Q}_{k-2}\right|$ 的最大值 $c_2$ upper bound 它
  3. 对于指数外部分，用 $\left|Q_{k-1}-{\mathcal{B}}^{\ast }{Q}_{k-2}\right|$ 的最小值 $c_1$ lower bound 它，以上三步得到
     $$w_k\propto \exp \left(\frac{-c_2-\gamma \left[P^{{\pi }_{k-1}}{\Delta }_{k-1}\right](s,a)}{\tau }\right)\frac{c_1}{{\lambda }^{\ast }}$$
  4. 把常数项 $c_1,c_2,{\lambda }^{\ast }$ 都简化掉，得到 $w_k$ 的可处理近似为
     $$w_k(s,a)\propto \exp \left(-\frac{\gamma \left[P^{{\pi }_{k-1}}{\Delta }_{k-1}\right](s,a)}{\tau }\right)$$

  注意替代 $|Q_k-Q^{\ast }|$ 时的推导，首先我们先找到了 $|Q_k-Q^{\ast }|$ 的上界为 $${\Delta }_k+\sum _{i=1}^k{\gamma }^{k-i}{\alpha }_i=\left|Q_k(s,a)-\left({\mathcal{B}}^{\ast }{Q}_{k-1}\right)(s,a)\right|+\gamma \left(P^{{\pi }_{k-1}}{\Delta }_{k-1}\right)(s,a)+\sum _{i=1}^k{\gamma }^{k-i}{\alpha }_i\ge |Q_k-Q^{\ast }|$$ 接下来又将 $\left|Q_k(s,a)-\left({\mathcal{B}}^{\ast }{Q}_{k-1}\right)(s,a)\right|+\gamma \left(P^{{\pi }_{k-1}}{\Delta }_{k-1}\right)(s,a)$ 替换为其上界 $c_2+\gamma \left(P^{{\pi }_{k-1}}{\Delta }_{k-1}\right)(s,a)$，然后直接作为 $|Q_k-Q^{\ast }|$ 上界了，在最终的结果中缺少了一个 $\alpha$ 的累计折扣和 ${\sum }_{i=1}^k{\gamma }^{k-i}{\alpha }_i$。注意 $${\alpha }_i=\frac{2R_{\max }}{1-\gamma }\underset{s}{\max }{\mathrm{D}}_{\mathrm{TV}}\left({\pi }_i(\cdot \mid s),{\pi }^{\ast }(\cdot \mid s)\right)$$ 其中

  1. $\frac{R_{\max }}{1-\gamma }={\sum }_{i=0}^{\infty }{\gamma }^i{R}_{\max }$，这是每一步都获取最大奖励 $R_{\max }$ 的无限长轨迹的最大收益
  2. $2{\max }_s{\mathrm{D}}_{\mathrm{TV}}\left({\pi }_i(\cdot \mid s),{\pi }^{\ast }(\cdot \mid s)\right)$ 这是 ${\pi }^{\ast }(\cdot \mid s)$ 和 ${\pi }_i(\cdot \mid s)$ 在整个动作空间上的总差距的最大值

  也就是说 ${\alpha }_i$ 表示了第 $i$ 轮迭代时策略 ${\pi }_i$ 和最优策略 ${\pi }^{\ast }$ 能对价值估计起到的影响的上界，这应该不是一个小数目，所以我不太清楚为何此处可以忽略掉它。但仔细想想这个 ${\mathrm{D}}_{\text{TV}}$ 好像也没法计算（因为 ${\pi }^{\ast }$ 不知道），而且这个值是和 $(s,a)$ pair 无关的一个常数，可能这里可能是先替代再简化掉了

• 最后我们可以直观地理解一下公式，看看我们要强调那些样本

  1. 先看原始形式
     $$\frac{q_k^{\ast }(s,a)}{{\mu }_k(s,a)}\propto \exp \left(\frac{-\left|Q_k-Q^{\ast }\right|(s,a)}{\tau }\right)\frac{\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|(s,a)}{{\lambda }^{\ast }}$$ 这里 $\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|(s,a)$ 是 Bellman 更新本身决定的无法控制，所以我们想强调的是那些 $\left|Q_k-Q^{\ast }\right|(s,a)$ 较小的 $(s,a)$，也就是对当前估计精度较高的样本给与更高的权重
  2. 再看替代后的可处理形式
     $$w_k(s,a)\propto \exp \left(-\frac{\gamma \left[P^{{\pi }_{k-1}}{\Delta }_{k-1}\right](s,a)}{\tau }\right)$$ 在第 $k$ 轮迭代时使用这个 $w_k$ 对损失加权，更新后得到 $Q_k$。其中起作用的主要是 ${\Delta }_{k-1}$ 项，注意其定义
     $${\Delta }_k(s,a)=\left|Q_k(s,a)-\left({\mathcal{B}}^{\ast }{Q}_{k-1}\right)(s,a)\right|+\gamma \left(P^{{\pi }_{k-1}}{\Delta }_{k-1}\right)(s,a)$$ ${\Delta }_{k-1}$ 记录的是前 $k-1$ 轮迭代中 Bellman 更新时误差的累计折扣和，这个误差完全是由于神经网络的泛化性导致的。如果是表格型算法且 batch 设为 1，这里的 $\Delta$ 将始终为 0，$w_k$ 全部为 1，相当于没有做加权。也就是说作者的方法实质上只解决了 “神经网络泛化性导致的价值误差”，没有解决 “由于 TD target 中累计误差所导致的价值误差”

     分析到这里再往回看忽略的 $\alpha$ 项，它其实可以表示这里缺失的部分

2.3 伪代码

• 仅体现核心思路的伪代码
  
• 实验时使用的更加 practical 的伪代码如下
  
  注意，其中的变化有
  1. 使用 target network 减少价值的高估
  2. 引入一个policy network来处理连续控制任务
  3. 设置了一个可以自动调整 $q_k=\arg {\min }_q-{\mathbb{E}}_{q(s,a)}[\log p_k(s,a)]+\tau D_{KL}(q(s,a)||\mu (s,a))$ 中温度参数 $\tau$ 的方案，注意到 $\tau$ 是追踪 $\Delta$ 的均值的，当累计偏差 $\Delta$ 较大时就调大 $\tau$，使 $q_k$ 更靠近 ${\mu }_k$ 来减小偏差

3. 实验

• 作者在 grid16（离散控制）、MetaWorld（很难的连续控制）、MT10（多任务设置）、Atari（经典游戏控制） 等环境中进行测试，由于本文本质是一个非均匀重放方法，主要的对比方法是 PER 和 DQN（均匀重放），为了体现性能优势还对比了 SAC，总之就是都有性能提升，具体结果请参考原文

4. 总结

1. 分析部分写得很不错，配合可视化例子，说理很清晰，并配有实验结果支持其发现。作者指出的问题也是一个非常重要但常常被忽视的问题，值得进一步探索
2. 可惜的是，虽然作者用很多篇幅说明价值估计误差是由于 “TD target 中累计误差” 和 “神经网络泛化性” 共同导致的，但是其提出的方法在做替代后其实只修正了神经网络泛化性导致的偏差，因此仍然有改进空间，尽管如此，其计算得到的 $p_k$ 表达式是准确的，这很有指导意义
3. 本文的理论证明部分写得不错，注意到计算时遇到了很多无法计算的项，作者在放缩时巧妙选择了可以调整的部分，把这些项都放缩掉了；另外那个对于不精确权重进行 “降权” 放缩的思想也值得学习

5. 关键结论的证明

• 本节给出 2.2.2 节中最优纠正分布 $p_k$ 的证明，公式编号和原文保持一致。优化目标是
  $$\begin{array}{rl}& \underset{p_k}{\min }{\mathbb{E}}_{d^{{\pi }_k}}\left[\left|Q_k-Q^{\ast }\right|\right]\\ & \text{ s.t. }{Q}_k=\arg \underset{Q}{\min }{\mathbb{E}}_{p_k}\left[{\left(Q-{\mathcal{B}}^{\ast }{Q}_{k-1}\right)}^2\right],\sum _{s,a}{p}_k(s,a)=1,\forall s,a{p}_k(s,a)\ge 0\end{array}\text{\hspace{1em}(8)}$$

  1. 引入 Fenchel-Young Inequality：$\forall x,yx,y\in {\mathbb{R}}^d$，对任意凸函数 $f$ 及其 Fenchel 共轭 $f^{\ast }$，有
     $${xx}^{\top }yy\le f(xx)+f^{\ast }(yy)$$ 这个不等式是显然的，因为共轭函数的定义就是 $f^{\ast }(yy)=\sup (x^{\top }y{x}^{\top }y-f(xx))$。注意到优化目标正是 $d^{{\pi }_k}$ 和 $\left|Q_k-Q^{\ast }\right|$ 两个向量内积的形式，所以带入 Fenchel-Young Inequality，得到
     $${\mathbb{E}}_{d^{{\pi }_k}}\left[\left|Q_k-Q^{\ast }\right|\right]\le f(\left|Q_k-Q^{\ast }\right|)+f^{\ast }(d^{{\pi }_k})\text{\hspace{1em}(9)}$$ 由于两边都在 $Q_k=Q^{\ast }$ 时取得最小值，所以可以用 (9) 中右式的 upper bound 代替 (8) 中的优化目标，求解这个松弛后的优化问题。为了便于处理，$f$ 选择为 $\text{soft-min}$ 函数
     $$f(x)=-\log (\sum _i{e}^{-x_i}),f^{\ast }(y)=\mathcal{H}(y)\text{\hspace{1em}(10)}$$ 这种选择下 $f^{\ast }$ 和香农熵的形式一致，这意味替换 (8) 中优化目标后，我们要同时最小化边际状态动作折扣分布 $d^{{\pi }_k}$ 的熵。为了避免优化得到的 $p_k$ 使得 $d^{{\pi }_k}$ 的熵大幅下降，作者使用 $(s,a)$ 均匀分布的熵 $\mathcal{H}(\mathcal{U})$ 作为 $\mathcal{H}(y)$ 的 upper bound 代替，这样 $f^{\ast }$ 项就变成常数可以省略了，最终得到的优化问题为
     $$\begin{array}{rl}& \underset{p_k}{\min }-\log \left(\sum _{s,a}\exp \left(-\left|Q_k-Q^{\ast }\right|(s,a)\right)\right)\\ & s.t.Q_k=\arg \underset{Q}{\min }{\mathbb{E}}_{p_k}\left[{\left(Q-{\mathcal{B}}^{\ast }{Q}_{k-1}\right)}^2\right],\sum _{s,a}{p}_k(s,a)=1,\forall s,a{p}_k(s,a)\ge 0\end{array}\text{\hspace{1em}(11)}$$

  2. 计算拉格朗日函数：使用拉格朗日乘子法解优化问题 (11)，写出拉格朗日函数
     $$\mathcal{L}\left(p_k;\lambda ,\mu \right)=-\log \left(\sum _{s,a}\exp \left(-\left|Q_k-Q^{\ast }\right|(s,a)\right)\right)+\lambda \left(\sum _{s,a}{p}_k(s,a)-1\right)-{\mu }^T{p}_k\text{\hspace{1em}(12)}$$ 接下来需要计算梯度 $\frac{\partial \mathcal{L}}{\partial p_k}=\frac{\partial \mathcal{L}}{\partial Q_k}\frac{\partial Q_k}{\partial p_k}$

  3. 使用 implicit function theorem (IFT)： 考虑如何计算 $\frac{\partial Q_k}{\partial p_k}$，这是两个长 $|\mathcal{S}|\times |\mathcal{A}|$ 向量间求导，最终会得到 $(|\mathcal{S}|\times |\mathcal{A}|)\times (|\mathcal{S}|\times |\mathcal{A}|)$ 的矩阵，注意 $Q_k$ 是一个对应元素相乘的形式，不好用求导公式，可以根据定义从元素对元素求导的角度出发。这里为了简化运算使用隐函数求导法，先找隐函数，假设 $Q_k$ 满足 $$Q_k=\arg \underset{Q}{\min }{\mathbb{E}}_{p_k}\left[{\left(Q-{\mathcal{B}}^{\ast }{Q}_{k-1}\right)}^2\right]$$ 则此处对 $Q_k$ 的梯度为零向量（数对向量求导得到等尺寸向量），这就是目标隐函数，即
     $$\begin{array}{rl}F(p_k,Q_k)& ={\left[\begin{array}{ccc}2p_k(s_0,a_0)[Q_k(s_0,a_0)-{\mathcal{B}}^{\ast }{Q}_{k-1}(s_0,a_0)]& \dots & 2p_k(s_{|\mathcal{S}|},a_{|\mathcal{A}|})[Q_k(s_{|\mathcal{S}|},a_{|\mathcal{A}|})-{\mathcal{B}}^{\ast }{Q}_{k-1}(s_{|\mathcal{S}|},a_{|\mathcal{A}|})]\end{array}\right]}^{\top }\\ & =\text{Diag}(Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1})p_k\\ & =\text{Diag}(p_k)(Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1})\\ & ={00}_{(|\mathcal{S}|\times |\mathcal{A}|)\times 1}\end{array}$$ 利用隐函数求导法，有
     $$\begin{array}{c}{H}_Q=2\mathrm{Diag}\left(p_k\right)H_{Q,p_k}=2\mathrm{Diag}\left(Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right)\\ \frac{\partial Q_k}{\partial p_k}=-{\left[H_Q\right]}^{-1}{H}_{Q,p_k}=-\mathrm{Diag}\left(\frac{Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}}{p_k}\right)\end{array}\text{\hspace{1em}(14)}$$

  4. 计算最优 $p_k$：令 $\frac{\partial \mathcal{L}(p_k;\lambda ,\mu )}{\partial p_k}=00$ 来求解最优 $p_k$（本质是对偶问题中的内层极小化问题），这是数对向量求导，还是按定义法从元素对元素求导角度考虑
     $$\frac{\partial \mathcal{L}\left(p_k;\lambda ,\mu \right)}{\partial p_k}=0\Rightarrow \frac{\mathrm{sgn}\left(Q_k-Q^{\ast }\right)\exp \left(-\left|Q_k-Q^{\ast }\right|(s,a)\right)}{{\sum }_{s^{\prime },a^{\prime }}\exp \left(-\left|Q_k-Q^{\ast }\right|\left(s^{\prime },a^{\prime }\right)\right)}\cdot \frac{\partial Q_k}{\partial p_k}+\lambda -{\mu }_{s,a}=0\text{\hspace{1em}(15)}$$带入上面计算的 $\frac{\partial Q_k}{\partial p_k}$ 得到
     $$p_k(s,a)=\frac{\mathrm{sgn}\left(Q_k-Q^{\ast }\right)\exp \left(-\left|Q_k-Q^{\ast }\right|(s,a)\right)}{{\sum }_{s^{\prime },a^{\prime }}\exp \left(-\left|Q_k-Q^{\ast }\right|\left(s^{\prime },a^{\prime }\right)\right)}\cdot \frac{(Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1})(s,a)}{\mu (s,a)-\lambda }$$当最优解存在且与原问题一致时，KKT条件成立，有 ${\mu }^{\ast }(s,a)p_k(s,a)=0(\forall s,a)$，令所有 $(s,a)$ 都有概率访问到，即 $p_k(s,a)>0$（极值点是约束面的内点），则 ${\mu }^{\ast }(s,a)=0$，且外层最大化解得的 ${\lambda }^{\ast }$ 要满足 $p_k(s,a)>0$，有
     $$p_k(s,a)\propto \exp \left(-\left|Q_k-Q^{\ast }\right|(s,a)\right)\frac{\left|Q_k-{\mathcal{B}}^{\ast }{Q}_{k-1}\right|(s,a)}{{\lambda }^{\ast }}\text{\hspace{1em}(16)}$$