强化学习笔记（2）—— 多臂赌博机

云端FFF

已于 2022-09-28 15:48:47 修改

阅读量649

点赞数 2

分类专栏： # 强化学习文章标签：算法贪心算法

于 2021-07-13 03:40:19 首次发布

本文链接：https://blog.csdn.net/wxc971231/article/details/118612486

版权

强化学习专栏收录该内容

21 篇文章 28 订阅

订阅专栏

参考：Richard S.Sutton 《Reinforce Learning》第2章
本节，我们在只有一个状态的简化情况下讨论强化学习中评估与反馈的诸多性质，在RL研究早期，很多关于评估性反馈的研究都是在这种 “非关联性的简化情况” 下进行的

1. k 臂赌博机问题

1.1 问题描述

想象你面对一台特殊的老虎机，它有k个摇臂，每拉动一个摇臂，都会落下一些金币。每个拉杆都对应一个金币收益的期望，我们称此为这个动作的 “价值”。那么，应该使用什么策略，才能在有限的尝试次数中获得最多金币呢？
如果你知道每个动作的价值，那么解决 k 赌博机非常简单：每次选择最高价值动作即可。但当不知道动作价值时，问题就变得复杂起来。

1.2 十臂测试平台

假设赌博机有十个拉杆，某个赌博机示例形式化描述如下
1. 每个动作 $a$ 的真实价值 $q_*(a)$ 从标准正态分布 $N (0, 1)$ 中采样得到，再将此动作的收益分布设定为正态分布 $N(q_*(a),1)$
2. 在一个赌博机问题上进行 $T$ 个时刻的交互，称为 “一轮实验”，使用 $N$ 个不同设定的赌博机问题独立重复实验 $N$ 轮次，即得到对这个学习算法平均表现的评估。为了提升评估准确度，测试量不宜太小，比如取 $T = 1000, N = 2000$

1.3 难点：平衡开发和试探

稍微对问题进行一些定义，将在时刻 t 时选择的动作记作 $A_t$ ，并将对应的收益记作 $R_t$ ，任意动作 $a$ 对应的价值（即收益的期望）记作 $q_*(a)$ ，即
$q_*(a) \doteq \mathbb{E}[R_t|A_t=a]$ 虽然我们不知道 $q_*(a)$ 的具体值，但我们可以进行估计，将 t 时刻对动作 $a$ 的价值估计记作 $Q_t(a)$ ，我们希望它接近 $q_*(a)$
如果我们持续对动作价值进行估计，那么任一时刻都会至少有一个动作的估计价值是最高的，我们将这些对应最高估计价值的动作成为 贪心动作。在选择动作时，有两种选择
1. 开发：利用当前所知的关于动作价值的知识，从贪心动作中选择一个执行
2. 试探：选择某个非贪心动作执行
显然，“开发” 可以最大化当前时刻的期望收益，但是合理地 “试探” 从长远来看可能带来总体收益的最大化，因为 “试探” 有助于我们更准确地估计当前非贪心动作的价值，进而找到真正的最优动作。注意，同一次动作选择时，开发和试探是不可能同时进行的，这就要求我们在开发和试探间进行平衡
在一个具体问题中，对于不同的数学建模，有多种复杂的方法可以直接求解最好的平衡方法，但是这些方法往往都对平稳情况和先验知识做出了很强的假设，在复杂一些的问题中，这些假设要么难以满足，要么难以验证，使得这些方法的最优性或有界损失性缺乏保证。本文中讨论的方法避开了这些强假设，虽然性能稍差，但是通用性更强，且易于推广到真正的强化学习问题。
平衡开发和试探是强化学习中的一个关键问题，k 臂赌博机的简单抽象让我们可以清楚地了解这一点。

2. 动作-价值方法

2.1 采样平均方法

我们使用对动作价值的估计作为选择动作的指导，这类方法统称为 “动作-价值方法”
如前所述，每个动作的价值为器收益的期望，欲估计动作，一个直观的想法就是使用 “采样平均方法”：使用实际收益的均值来估计期望，即
$Q_t(a) \doteq \frac{t时刻前执行动作a获得的总收益}{t时刻前执行动作a的次数} = \frac{\sum_{i=1}^{t-1}R_i \Bbb{1}(A_i=a)}{\sum_{i=1}^{t-1} \Bbb{1}(A_i=a)}$ 我们可以给 $Q_t(a)$ 设置任意默认初值（比如0），根据大数定律，当分母趋向于无穷大时， $Q_t(a)$ 将收敛到 $q_*(a)$

2.2 增量式实现

下面我们讨论一种增量式计算方法，以高效地计算上述均值。为了简化标记，我们这里仅关注单个动作，令 $R_i$ 表示这一动作被选中 $i$ 次后获得的收益， $Q_n$ 表示选中 n-1 次后对其动作价值的估计，则有
$Q_n \doteq \frac{R_1+R_2+...+R_{n-1}}{n-1}$ 这种计算方式要求维护所有收益记录，然后在每次需要估计价值时计算，随着记录增加，内存和计算资源的需求随之增长。
使用下面这种递推式计算方法，可以以小而恒定的计算资源来更新均值，给出 $Q_n$ 和第n次收益 $R_n$ ，价值更新如下
$\begin{aligned} Q_{n+1} &= \frac{1}{n} \sum_{i=1}^n R_i \\ &= \frac{1}{n}(R_n+\sum_{i=1}^{n-1}R_i) \\ &= \frac{1}{n}(R_n+(n-1)\frac{1}{(n-1)}\sum_{i=1}^{n-1}R_i) \\ &= \frac{1}{n}(R_n+(n-1)Q_n) \\ &= \frac{1}{n}(R_n + nQ_n-Q_n) \\ &= Q_n + \frac{1}{n}[R_n-Q_n] \end{aligned}$ 这个式子对于 n=1 也有效，可得 $Q_2 = R_1$ ，对于每个新的收益，只需要存储 $Q_n$ 和 n 即可
上式的一般形式为
$\begin{aligned} 新估计值 &\leftarrow 旧估计值 + 步长 \times [目标 - 旧估计值] \\ &\leftarrow 旧估计值 + 步长 \times 误差 \end{aligned}$ 虽然 “目标” 可能存在噪声，但我们假定 “目标” 会告诉我们前进的方向，上述例子中，“目标” 就是第 n 次的收益
值得注意的是，“步长” 可能随时间变化，比如上述例子中的步长就是关于动作 a 执行次数 n 的函数 $\frac{1}{n}$ ，通常把步长记作 $\alpha$ ，或更普适地记作 $\alpha_t(a)$

2.3 $\epsilon$ -贪心

现在考虑如何利用动作价值的估计来选择动作
贪心：总是贪心地选择目前具有最大价值的动作，即
$A_t \doteq \argmax_{a} Q_t(a)$ 这种策略只最大化眼前的收益，但是完全不去尝试目前看来劣质的动作，事实上，如果进行一些试探，很可能发现现在看来劣质的动作其实更好
ϵ-贪心：大部分时候表现得贪心，但偶尔（以小概率 $\epsilon$ ）以独立与动作-价值估计值的方式从所有动作中等概率地做出随机选择。这种方式的好处在于：如果时刻可以无限长，则所有动作都会被无限次采样，从而确保所有的 $Q_t(a)$ 收敛到 $q_*(a)$ ，这也意味着选择最优动作的概率会收敛到大于 $1-\epsilon$
ϵ-贪心相比普通贪心方法的优势依赖于任务
1. 假设任务是一个确定性任务，收益方差为0（只需一次尝试即可找出动作的真实收益），这时普通贪心可能效果更好，因为它能很快找到最优动作，然后再也不会进行试探
2. 假设任务是一个非确定性任务，收益方差为很大，那么显然 $\epsilon$ -贪心更有利于跳出局部最优，效果好于普通贪心
3. 即使对于确定性任务，如果任务是非平稳的（动作的价值可能会不停变化），那么 $\epsilon$ -贪心也更有利于及时找出新的贪心动作，效果好于普通贪心。事实上，非平稳性是强化学习中常常遇到的情况。
总之，对于绝大多数情况，尤其是非平稳、非确定性任务， $\epsilon$ -贪心都由于普通贪心方法

2.4 一个简单的多臂赌博机算法

用 $\epsilon$ -贪心选择动作，用采样平均方法评估动作价值

2.5 测试

用 1.3 节描述的十臂测试平台对比动作选择时的 ϵ-贪心和贪心方法。动作价值估计都使用采样平均方法，实验结果如下
1. 贪心：在最初增长得略快一点，但随后稳定在较低水平。如下方图所示，贪心方法只在约 $\frac{1}{3}$ 的任务中找到最优动作，其他情况下最初采样的动作很差，贪心方法无法跳出优解
2. ϵ-贪心：持续试探提升了找到最优动作的机会，其表现优于贪心。当 $\epsilon$ 值较大时，试探更多，但是选择最优动作的概率会较低。如图所示， $\epsilon$ 值较大时性能提升更快，而 $\epsilon$ 值较小时收敛性能更好。为了充分利用这一特点，可以随着时刻推移逐步减小 $\epsilon$ 取值

示例代码

# 十臂赌博机
import numpy as np
import matplotlib.pyplot as plt

class Bandit:
    def __init__(self,K):
        self.K = K

        self.values = np.random.randn(K)            # 从标准正态分布采样K个拉杆的收益均值
        self.bestAction = np.argmax(self.values)    # 最优动作索引

        self.QValues = np.zeros(K)  # 价值评估值 
        self.N = np.zeros(K)        # 动作选择次数

        self.setPolicy()            # 缺省策略为greedy

    def setPolicy(self,mode='greedy',epsilon=0):
        self.mode = mode
        self.epsilon = epsilon
        
    def greedy(self):
        return np.random.choice([a for a in range(self.K) if self.QValues[a] == np.max(self.QValues)])

    def epsilonGreedy(self):
        if np.random.binomial(1,self.epsilon) == 1:
            return np.random.randint(self.K)
        else:
            return self.greedy()

    def takeAction(self):
        if self.mode == 'greedy':
            return self.greedy()
        else:
            return self.epsilonGreedy()

    def play(self,times):
        G = 0   # 当前收益
        B = 0   # 当前最优选择次数
        returnCurve = np.zeros(times)       # 收益曲线
        proportionCurve = np.zeros(times)   # 比例曲线
        
        self.QValues = np.zeros(self.K)
        self.N = np.zeros(self.K)

        for i in range(times):
            a = self.takeAction()
            r = np.random.normal(self.values[a],1,1) 
            B += a == self.bestAction

            self.N[a] += 1
            self.QValues[a] += 1/self.N[a]*(r-self.QValues[a])  # 增量式计算均值

            returnCurve[i] = G/(i+1)
            proportionCurve[i] = B/(i+1)
            G += r
    
        return returnCurve,proportionCurve

if __name__ == '__main__':
    K = 10          # 摇臂数
    Num = 100       # 赌博机数量
    times = 2000    # 交互次数
    paraList = [('greedy',0,'greedy'),('epsilon',0.1,'0.1-greedy'),('epsilon',0.01,'0.01-greedy')]

    # 解决 plt 中文显示的问题
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    
    fig = plt.figure(figsize=(12,8))
    a1 = fig.add_subplot(2,1,1,label='a1')
    a2 = fig.add_subplot(2,1,2,label='a2')

    a1.set_xlabel('训练步数')
    a1.set_ylabel('平均收益')
    a2.set_xlabel('训练步数')
    a2.set_ylabel('最优动作比例')
    
    # 实例化 Num 个赌博机
    bandits = []
    for i in range(Num):
        bandit = Bandit(K)
        bandit.setPolicy('greedy')
        bandits.append(bandit)

    # 测试三种策略
    for paraMode,paraEpsilon,paraLabel in paraList:
        aveRCurve,avePCurve = np.zeros(times),np.zeros(times)
        for i in range(Num):
            print(paraLabel,i)
            bandits[i].setPolicy(paraMode,paraEpsilon)
            returnCurve,proportionCurve = bandits[i].play(times)
            aveRCurve += 1/(i+1)*(returnCurve-aveRCurve)        # 增量式计算均值
            avePCurve += 1/(i+1)*(proportionCurve-avePCurve)    # 增量式计算均值

        a1.plot(aveRCurve,'-',linewidth=2, label=paraLabel)
        a2.plot(avePCurve,'-',linewidth=2, label=paraLabel)
    
    a1.legend(fontsize=10)  # 显示图例，即每条线对应 label 中的内容
    a2.legend(fontsize=10)  

    plt.show()

3. 跟踪一个非平稳问题

上述我们讨论的都是平稳问题（stationary bandit problems），即收益的概率分布不会随着时间变化的问题，如果赌博机的收益概率随着时间变化，前述方法就不再合适。事实上，在强化学习中，我们经常会遇到这种非平稳问题（nonstationary Problem）

3.1 指数近因加权平均

在非平稳情况下，一种合理的处理方式是给近期的收益赋予较大的权重，最流行的方法之一是使用固定的步长，这时，如下更新动作价值估计
$Q_{n+1} \doteq Q_n+\alpha[R_n-Q_n]$ 其中，步长参数 $\alpha \in (0,1]$ 是一个常数
这本质上是进行了一个加权平均处理，把 $Q_{n+1}$ 展开
$\begin{aligned} Q_{n+1} &= Q_n+\alpha[R_n-Q_n] \\ &= \alpha R_n + (1-\alpha) Q_n\\ &= \alpha R_n + (1-\alpha)[ \alpha R_{n-1} + (1-\alpha) Q_{n-1}] \\ &= \alpha R_n + (1-\alpha) \alpha R_{n-1} + (1-\alpha)^2 Q_{n-1} \\ &= \alpha R_n + (1-\alpha) \alpha R_{n-1} + (1-\alpha)^2 R_{n-2} +...+(1-\alpha)^{n-1}\alpha R_1+(1-\alpha)^n Q_1\\ &= (1-\alpha)^n Q_1+\sum_{i=1}^n \alpha(1-\alpha)^{n-i} R_i \end{aligned}$ 可见 $Q_{n+1}$ 是对过去收益 $R_i(i=1,2,...,n)$ 和初始估计值 $Q_1$ 的加权和，分析权重，有

$\begin{aligned} (1-\alpha)^n + \sum_{i=1}^n \alpha(1-\alpha)^{n-i} &= (1-\alpha)^n+\alpha[(1-\alpha)^0\frac{(1-\alpha)^n-1}{-\alpha}] \\ &= (1-\alpha)^n + 1- (1-\alpha)^n \\ &= 1 \end{aligned}$ 权重之和为1，因此 $Q_{n+1}$ 是对过去收益 $R_i(i=1,2,...,n)$ 和初始估计值 $Q_1$ 的加权平均，赋予 $R_i$ 的权重随着相隔次数的增加而递减，如果 $1-\alpha=0$ ，根据 $0^0=1$ ，所有权重都赋予最近收益 $R_n$ 。注意到收益权重以指数形式递减，因此这个方法有时也称为 “指数近因加权平均”

3.2 收敛条件

设 $\alpha_n(a)$ 表示第n次选择动作 $a$ 并得到收益时，更新价值估计的步长参数。注意到，当选择 $\alpha_n(a) = \frac{1}{n}$ 时，我们得到 2.1 节中的 “采样平均方法”，大数定律保证它可以收敛到真值。然而，不一定所有的 $\{\alpha_n(a)\}$ 序列都满足收敛条件
随机逼近理论中的一个著名结果给出了保证收敛概率为1所需的条件
$\sum_{n=1}^\infin \alpha_n(a) = \infin 且 \sum_{n=1}^\infin\alpha_n^2(a) < \infin$
1. $\sum_{n=1}^\infin \alpha_n(a) = \infin$ ：保证有足够大的步长，最终克服任何初始条件或随机扰动
2. $\sum_{n=1}^\infin\alpha_n^2(a) < \infin$ ：保证最终步长变小，以保证收敛
注意到
1. 采样平均：步长随时刻变化， $\alpha_n(a) = \frac{1}{n}$ 。这时 $\sum_{n=1}^\infin\frac{1}{n}$ 是调和级数，发散到 $\infin$ ，满足条件1； $\sum_{n=1}^\infin\frac{1}{n^2}$ 是p=2的p级数，收敛，因此采样平均法最终可以收敛
2. 指数近因加权平均：常数步长参数 $\alpha_n(a) = \alpha$ 。这时虽然满足第一个条件，但第二个条件不满足，说明估计值永远不会收敛，而是会随着最近得到收益而变化，这正是非平稳问题中我们想要的特性。

3.3 测试

利用十臂测试平台对比采样平均方法和指数近因加权平均方法。这个测试中，所有动作初始的真实价值 $q_*(a)$ 设为 0，在每一步迭代时都加上一个从正态分布 $N (0, 0.01)$ 采样的增量。除了估计动作价值方式不同外，选择动作时两种方法都使用 $\epsilon=0.1$ 的 $\epsilon$ -贪心方法

代码

# 十臂赌博机
import numpy as np
import matplotlib.pyplot as plt

class Bandit:
    def __init__(self,K):
        self.K = K

        self.values = np.zeros(K)                   # 所有动作初始价值为0
        self.bestAction = np.argmax(self.values)    # 最优动作索引

        self.QValues = np.zeros(K)  # 价值评估值 
        self.N = np.zeros(K)        # 动作选择次数

        self.setPolicy()            # 缺省策略为greedy

    def setPolicy(self,mode='SA',epsilon=0.1):
        self.mode = mode
        self.epsilon = epsilon

    def takeAction(self):
        if np.random.binomial(1,self.epsilon) == 1:
            return np.random.randint(self.K)
        else:
            return np.random.choice(np.argwhere(self.QValues == np.max(self.QValues)).flatten().tolist())
    

    def play(self,times):
        G = 0   # 当前收益
        B = 0   # 当前最优选择次数
        returnCurve = np.zeros(times)       # 收益曲线
        proportionCurve = np.zeros(times)   # 比例曲线
        
        self.QValues = np.zeros(self.K)
        self.N = np.zeros(self.K)

        for i in range(times):
            self.values += np.random.normal(0,0.01,self.K)      # 价值随机游走
            self.bestAction = np.argmax(self.values)

            a = self.takeAction()
            r = np.random.normal(self.values[a],1,1) 
            
            if self.mode == 'SA':
                self.N[a] += 1
                self.QValues[a] += 1/self.N[a]*(r-self.QValues[a])  # 采样平均
            else:
                self.QValues[a] += 0.1*(r-self.QValues[a])          # 指数近因加权平均

            returnCurve[i] = G/(i+1)
            proportionCurve[i] = B/(i+1)
            G += r
            B += a == self.bestAction

        return returnCurve,proportionCurve

if __name__ == '__main__':
    K = 10          # 摇臂数
    Num = 200       # 赌博机数量
    times = 10000   # 交互次数
    paraList = [('SA',0.1,'Sample Average'),('ERW',0.1,'Exponential Recency Weighted')]

    # 解决 plt 中文显示的问题
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    
    fig = plt.figure(figsize=(12,8))
    a1 = fig.add_subplot(2,1,1,label='a1')
    a2 = fig.add_subplot(2,1,2,label='a2')

    a1.set_xlabel('训练步数')
    a1.set_ylabel('平均收益')
    a2.set_xlabel('训练步数')
    a2.set_ylabel('最优动作比例')
    
    # 实例化 Num 个赌博机
    bandits = []
    for i in range(Num):
        bandit = Bandit(K)
        bandit.setPolicy('greedy')
        bandits.append(bandit)

    # 测试策略
    for paraMode,paraEpsilon,paraLabel in paraList:
        aveRCurve,avePCurve = np.zeros(times),np.zeros(times)
        for i in range(Num):
            print(paraLabel,i)
            bandits[i].setPolicy(paraMode,paraEpsilon)
            returnCurve,proportionCurve = bandits[i].play(times)
            aveRCurve += 1/(i+1)*(returnCurve-aveRCurve)        # 增量式计算均值
            avePCurve += 1/(i+1)*(proportionCurve-avePCurve)    # 增量式计算均值

        a1.plot(aveRCurve,'-',linewidth=2, label=paraLabel)
        a2.plot(avePCurve,'-',linewidth=2, label=paraLabel)
    
    a1.legend(fontsize=10)  # 显示图例，即每条线对应 label 中的内容
    a2.legend(fontsize=10)  

    plt.show()

测试结果如下，可见指数近因加权平均法在非平稳问题上远优于采样平均方法

3.4 无偏恒定步长技巧

上述的指数近因加权平均方法，由于使用恒定步长，虽然适用于非平稳问题，但其对价值的估计是有偏的。
要兼顾恒定步长和无偏估计，可以使用如下步长
$\beta_n \doteq \frac{\alpha}{\bar{o}_n}$ 其中 $\alpha>0$ 是一个传统的恒定步长， $\bar{o}_n$ 是一个从零时刻开始计算的修正系数

$\bar{o}_n \doteq \bar{o}_{n-1} + \alpha(1-\bar{o}_{n-1}),对 n\geq 0,满足 \bar{o}_0 \doteq 0$

4. 乐观初始价值

上述我们的方法都在一定程度上依赖于初始设定的动作价值估计 $Q_1(a)$ ，这对价值估计引入了偏差。对于采样平均法，最终可以逐渐修正到无偏估计；对于指数近因加权平均法，偏差会逐渐减少但不会消失。通过这些初始估计，我们可以简单地设置关于预期收益水平的先验知识。
把所有的初始价值估计都设为 “过于乐观”，是鼓励智能体进行试探的一个小技巧。因为无论智能体选择哪个动作，收益都比最初的估计要小，这导致智能体感到 “失望”，进而转向试探其他动作。其结果是，所有动作在估计值收敛前都被试探了好几次，即使每次都按贪心法选择动作，系统也会进行大量试探
这种鼓励试探的方法称为 乐观初始价值，需要注意的是，这不是一个鼓励试探的普适方法，因为其试探的驱动力天生是暂时的，一旦任务发生变化，这种方法就无法再提供帮助。
1. 对于平稳任务：这种技巧非常有效
2. 对于非怕平稳任务：不是很有效，事实让，任何仅仅估计初条件的方法对于一般的非平稳问题都不太有用。
利用十臂测试平台，赌博机设定同第 1.2 节，对比乐观初始价值的贪心方法和普通初始化的 $\epsilon$ -贪心的性能，如下
1. 乐观初始化技巧在初始阶段鼓励了试探，这使得贪心方法也能进行足够的试探，并找出最优动作。明确优动作后，由于不进行随机试探，智能体性能提升比 $\epsilon$ -贪心快很多。
2. 注意乐观初始化的曲线在早期有一个峰，我们可以推测最优动作的实际价值小于5，虽然早期找到了一回最优动作，但在若干次价值更新后，对最优动作价值的估计逐渐准确，此时没有充分更新的次优动作价值仍过于乐观，因此智能体又转向选择次优动作。

5. 基于置信度上界的动作选择（UCB）

因为对动作价值的估计总是存在不确定性，所以试探是必须的。 $\epsilon$ -贪心允许试探，但是其试探是盲目的。
在非贪心动作中，最好是根据它们的潜力来选择可能事实上最优的动作，这就要考虑它们的估计有多接近最大值，以及这些估计的不确定性。
综合考虑这两个因素，可以使用 “基于置信度上界的动作选择方法”（UCB），它根据下式选择动作
$A_t \doteq \argmax_a[Q_t(a)+c\sqrt{\frac{lnt}{N_t(a)}}]$
其中， $N_t(a)$ 代表时刻 $t$ 之前 a 被选择的次数，若 $N_t(a) = 0$ ，则认为a是满足最大化条件的动作之一
该方法思想源自 霍夫丁不等式Hoeffding's inequality，它给出了 “随机变量的和” 与其 “期望值” 偏差的概率上限。具体而言，令 $X_1,...,X_n$ 为 $n$ 个独立同分布的随机变量，取值范围 $[0, 1]$ ，其样本值的经验期望为 $\bar{x}_n=\frac{1}{n}\sum_{j=1}^n X_j$ ，则有
$P\big[\mathbb{E}[X]\geq \bar{x}_n+u\big]\leq \exp({-2nu^2})$ 其中 $u$ 代表当前经验期望的不确定度， $\geq$ 右边形成 $X$ 真实期望 $\mathbb{E}[X]$ 的一个上界，这个式子反映了该当前经验期不确定度超过 $u$ 的最大概率。把该不等式应用到多臂赌博机问题中，有
1. 真实价值 $Q (a)$ 相当于上面被估计的 $\mathbb{E}[X]$
2. 当前估计的经验期望 $\hat{Q}_t(a)=\frac{1}{N_t(a)}\sum_{i=1}^{N_t(a)}r_i(a)$ 相当于上面的 $\bar{x}_n$
3. 当前估计的不确定度 $u$ 记为 $\hat{U}_t(a)$ ，设 $p = \exp({-2N_t(a)U_t(a)^2})$ ，给定一个概率 $p$ 就能找到对应的不确定度为 $\hat{U}_t(a) = \sqrt{\frac{-\log p}{2N_t(a)}}$
这样处理后，可以直观地理解为：在当前时刻 $t$ ，真实价值 $Q (a)$ 和当前估计 $\hat{Q}_t(a)$ 的差距大于 $\hat{U}_t(a) = \sqrt{\frac{-\log p}{2N_t(a)}}$ 的概率不超过 $p$ ，当 $p$ 很小时 $\hat{Q}_t(a)+\hat{U}_t(a)$ 就成为 $Q (a)$ 的可靠上界。这样我们的策略就可以设计为 “挑选期望奖励上界最大的拉杆”，从而选择最有可能获得最大期望奖励的拉杆，即
$A_t = \argmax_{a} \big[\hat{Q}_t(a)+\hat{U}_t(a)\big]$ 在实际操作中，可以设 $p=\frac{1}{t}$ 使其逐渐减小，实现早期偏重探索，后期偏向利用的效果（类似 $\epsilon$ 逐渐减小的 $\epsilon$ -greedy），并用系数 $c$ 来控制不确定性的比重，并且在开方项分母加 1 来避免分母为 0，此时
$A_t =\argmax_a\big[\hat{Q}_t(a)+c\sqrt{\frac{lnt}{2(N_t(a)+1)}}\big]$
从直观上看 $\sqrt{\frac{lnt}{N_t(a)}}$ 项，随着动作a被选中次数 $N_t(a)$ 增加，这一项会随之减小，而选则其他动作时， $l n t$ 增大，这一项也随之增大，因此开方项是对动作a估计价值的不确定性或方差的度量，系数 c 决定置信水平。随着时间的流逝，所有动作最终都将被选中，但具有较低估计价值或已经被选中更多次的动作，被选中的概率较低
利用十臂测试平台，赌博机设定同第 1.2 节，对比 UCB 和 $\epsilon$ -贪心
1. UCB表现超过 $\epsilon$ -贪心，但它更难推广到其他更一般的学习问题中，一个困难是其处理非平稳问题时会变得很复杂；另一个问题是要处理大的状态空间
2. 注意到第11步时UCB方法有一个尖峰，这是由于：前10步中，总有动作的 $N_t(a) = 0$ ，满足最大化条件，因此这个阶段可以看作一轮试探。而第11步时，智能体根据第一轮试探结果贪心地选择，这个动作会不停被选择，直到其 $\sqrt{\frac{lnt}{N_t(a)}}$ 项减小到一定程度，才会被其他动作替代。这个被不停选择的动作可能是一个价值较高的动作，因此造成了尖峰。
从长远来看， $N_t$ 和 t 是同一个数量级，而 $lim_{t\to\infin} \frac{lnt}{t} =0$ ，因此 UCB 方法是 “渐进贪心” 的

6. 梯度赌博机

上述我们讨论的都是 “动作-价值” 方法，即使用对动作价值的估计作为选择动作的指导。这通常是一个好方法，但并不是唯一可用的方法。本节我们讨论一个基于随机梯度上升的动作选择算法

6.1 梯度赌博机算法

我们针对每个动作a考虑学习一个数值化的偏好函数 $H_t(a)$ 。偏好函数越大，动作就越频繁地被选择。需要注意的是，偏好函数并不是从 “收益” 的意义上提出的，而是从动作间比较优势的角度提出
利用偏好函数 $H_t(a)$ ，使用 softmax 分布定义 t 时刻各个动作被选中的概率为
$Pr\{A_t=a\} \doteq \frac{e^{H_t(a)}}{\sum_{b=1}^k e^{H_t(b)}} \doteq \pi_t(a)$ 在初始时刻，所有动作的初始值都设为相同（比如全为0），这时各个动作被选中的概率是相等的。
注意：当只有两个动作 ${a_1,a_2\}$ 的情况下，softmax 分布与 logistic 回归或 sigmoid 函数给出的结果相同
$Pr\{A_t=a_1\} = \frac{e^{H_t(a_1)}}{e^{H_t(a_1)}+e^{H_t(a_2)}} = \frac{1}{1+e^{-x}}\\$ 其中 $x = H_t(a_1)-H_t(a_2)$
在每个步骤中，选中动作 $A_t$ 并获得收益 $R_t$ 后，偏好函数按照以下方式更新
$\left\{ \begin{aligned} H_{t+1}(A_t) &\doteq H_t(A_t) + \alpha(R_t-\bar{R_t})(1-\pi_t(A_t)) &&,A_t是选中动作\\ H_{t+1}(a) &\doteq H_t(a) - \alpha(R_t-\bar{R_t})\pi_t(a) &&,a\neq A_t是非选中动作 \end{aligned} \right.$
1. 步长 $\alpha$ 是一个大于0的数
2. $\bar{R_t} \in \mathbb{R}$ 是时刻 t 内平均收益，可以使用前述的 “指数近因加权平均” 或 “采样平均” 方法计算。这被称为 “基准项”（baseline），它用于比较收益，若选中动作 $A_t$ 的收益 $R_t$ 高于 $\bar{R_t}$ ，那么未来选中 $A_t$ 的概率就会增大；反之则减小选中 $A_t$ 的概率，增大选中其他动作的概率。注意：基准项正是这个方法的核心，它代表当前选中动作相比历史平均动作的比较优势，若取消这一项（ $\bar{R_t} \doteq 0$ ），则此方法某种程度上又变回动作-价值方法
利用十臂测试平台进行测试，这个测试中所有动作的真实价值 $q_*(a)$ 从正态分布 $N (4, 1)$ 中采样得到，其他设定同第3节。步长 $\alpha$ 分别设定为0.1和0.4，对比基准项存在和不存在（ $\bar{R_t} \doteq 0$ ）时的性能

可见，基准项使得智能体可以马上适应新的收益水平，若取消基准项，性能显著下降。

6.2 本质：随机梯度上升

梯度赌博机算法可以理解为梯度上升的随机近似，这有助于我们深入理解此算法的本质

6.2.1 梯度上升算法

使用总体的期望收益作为性能的衡量指标，即
$\mathbb{E}[R_t] = \sum_x \pi_t(x)$
在精确的梯度上升算法中，每一个动作的偏好函数 $H_t(a)$ 更新增量与其对性能的影响成正比，而增量产生的影响可以用性能衡量指标对偏好函数的偏导数表示，即
$H_{t+1}(a) \doteq H_t(a) + \alpha\frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)}$
我们无法实现精确的梯度上升，因为真实的 $q_*(a)$ 是不知道的。但事实上，前文 7.1 节中提到的偏好函数更新方式，与这个更新方式是等价的，即梯度赌博机算法是梯度上升方法的一个实例

6.2.2 分析

把性能梯度展开
$\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} &= \frac{\partial}{\partial H_t(a)}[\sum_x\pi_t(x)q_*(x)] \\ &= \sum_xq_*(x)\frac{\partial \pi_t(x)}{\partial H_t(a)} \\ &= \sum_x(q_*(x)-B_t) \frac{\partial \pi_t(x)}{\partial H_t(a)} \end{aligned}$
其中 $B_t$ 称为 “基准项”，可以是任意不依赖于 $x$ 的标量。注意到概率之和 $\sum_x\pi_t(x) = 1$ 是一个常数，因此随着 $H_t(a)$ 的变化，一些动作的概率会增加和减少，但这些变化的总和为0，即 $\sum_x\frac{\partial \pi_t(x)}{\partial H_t(a)} = 0$ ，因此引入 “基准项” 后等号仍然成立。
接下来将求和公式中每项都乘以 $\pi_t(x)/\pi_t(x)$ ，转换为求期望
$\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} &= \sum_x \pi_t(x) (q_*(x)-B_t) \frac{\partial \pi_t(x)}{\partial H_t(a)}\frac{1}{\pi_t(x)} \\ &= \mathbb{E}_{A_t}[(q_*(A_t)-B_t) \frac{\partial \pi_t(A_t)}{\partial H_t(a)}\frac{1}{\pi_t(A_t)} ] \\ &= \mathbb{E}_{A_t}[(R_t-\bar{R_t}) \frac{\partial \pi_t(A_t)}{\partial H_t(a)}\frac{1}{\pi_t(A_t)} ] \end{aligned}$ 这里我们选择 $B_t = \bar{R_t}$ ，注意到有 $\mathbb{E}[R_t|A_t] = q_*(A_t)$ ，因此这里用 $R_t$ 代替 $q_*(A_t)$
下面展开偏导项 $\frac{\partial \pi_t(A_t)}{\partial H_t(a)}$ ，这里要用到商的求导法则
- 其中第四个等号推导使用了下式
  $\left\{ \begin{aligned} &\frac{\partial e^{H_t(x)}}{\partial H_t(a=x)} = e^{H_t(x)} \\ &\frac{\partial e^{H_t(x)}}{\partial H_t(a\neq x)} = 0 \end{aligned} \right.$
回代，有
$\begin{aligned} \frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)} &= \mathbb{E}_{A_t}[(R_t-\bar{R_t}) \frac{\partial \pi_t(A_t)}{\partial H_t(a)}\frac{1}{\pi_t(A_t)} ] \\ &= \mathbb{E}_{A_t}[(R_t-\bar{R_t})\pi_t(A_t)(\mathbb{1}_{a=A_t}-\pi_t(a))\frac{1}{\pi_t(A_t)} ] \\ &= \mathbb{E}_{A_t}[(R_t-\bar{R_t})(\mathbb{1}_{a=A_t}-\pi_t(a)) ] \end{aligned}$
这样，我们就把性能指标的梯度写成了 $(R_t-\bar{R_t})(\mathbb{1}_{a=A_t}-\pi_t(a))$ 关于 $A_t$ 的期望，这样我们就可以在每个时刻进行采样，再进行与采样成比例的更新，即
$\begin{aligned} H_{t+1}(a) = H_t(a) + \alpha (R_t-\bar{R_t})(\mathbb{1}_{a=A_t}-\pi_t(a)), 对所有a \end{aligned}$ 即

$\left\{ \begin{aligned} H_{t+1}(A_t) &\doteq H_t(A_t) + \alpha(R_t-\bar{R_t})(1-\pi_t(A_t)) &&,A_t是选中动作\\ H_{t+1}(a) &\doteq H_t(a) - \alpha(R_t-\bar{R_t})\pi_t(a) &&,a\neq A_t是非选中动作 \end{aligned} \right.$
这正是梯度赌博机算法中的更新公式，这样我们就证明了梯度赌博机算法是随机梯度上升算法的一种，这就保证了其有很强的收敛性
注意，对于 “基准项”，除了要求它不依赖于所选择动作外，不需要任何其他假设，我们可以将其设为0或1000，算法依然是随机梯度上升的特例。虽然 “基准项” 不影响算法的预期更新，但它确实影响更新值的方差，从而影响收敛速度。使用收益均值作为基准项可能不是最好的，但很简单，且在实践中表现良好

7. 关联搜索（上下文相关的赌博机）

到目前为止，前述内容都仅考虑了非关联任务，即不需要把不同的动作和不同的情境联系起来。前述所有内容都仅有一台赌博机，在这一台机器上，对于平稳任务，我们试图找到最优动作；对于非平稳任务，我们试图跟踪最优动作。这里仅仅只有一台机器，一个情境。
对于一个多情境任务，想象你面对五台不同的k摇臂赌博机，它们有着不同的颜色和价值设定，这种情况下，为了获取最多金币（收益），你必须根据根据不同情境来改变策略。比如，面对红色赌博机，选择1号拉杆；面对蓝色赌博机，选择2号拉杆…
以上是一个关联搜索任务的例子，它有两个核心特点
1. 智能体要使用试错学习去搜索最优动作
2. 智能体要把情境和最优动作关联在一起
在文献中，关联搜索任务常常被称为 “上下文相关的赌博机”，这种任务介于k摇臂赌博机任务和完整的强化学习任务之间
1. 类似完整的RL任务，它需要智能体学习一种策略，即根据不同的情境（状态）选择不同的动作
2. 类似kk摇臂赌博机，每个动作仅仅影响即时收益，而不影响下一时刻的收益与情境（状态）
对比

8. 总结

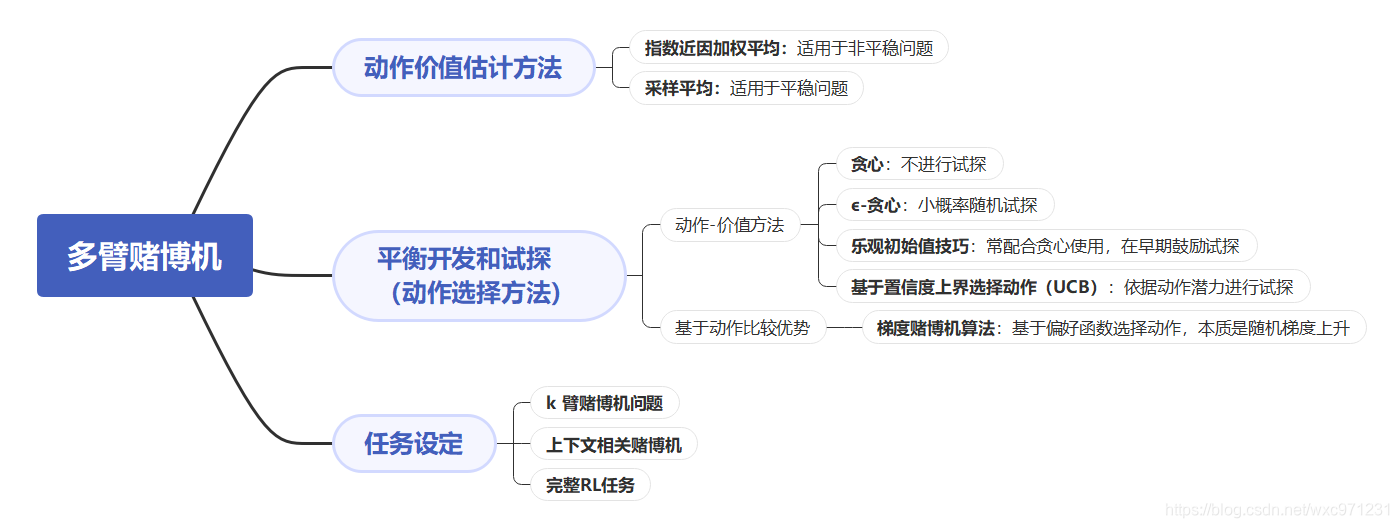
8.1 本文内容导图

在这里插入图片描述

8.2 对比所有动作选择方法

本章介绍了五种动作选择方法，我们在十臂测试平台上对比它们的性能。这个比较的困难之处在于，各个方法都有一个参数，难以进行有意义的比较。
为了进行对比，我们把每种算法的性能看作关于其参数的函数，这种类型的图表称为 “参数研究图”。下图总结了一个完整而精简的学习曲线，展示了每种算法和参数超过1000步的平均收益值，这个值与学习曲线下的面积成正比。
1. 图中每一个点表示特点算法在特定参数下执行超过1000步以后的平均收益
2. 注意 x 轴的参数变化是2的倍数，且以对数坐标表示
3. 如图所示，在这个问题上，UCB表现最好
在评估一种方法时，我们不仅要关注它在最佳参数设定上的表现，还要注意它对参数的敏感性，如图所示，所有这些算法都是相等不敏感的，在一系列参数值上表现良好。

8.3 更复杂的动作选择方法

对于k臂赌博机问题，平衡试探和开发的一个经典动作选择方法是计算一个名为 “Gittins指数” 的特殊函数，这为一些赌博机问题提供了一个最优的解决方案，而且比本文介绍的五种方法更具一般性，但前提是已知可能问题的先验分布。不幸的是，这种方法的理论和计算性都不能推广到完整强化学习问题
贝叶斯方法假定已知动作价值的初始分布，然后在每步之后更新分布，这样我们就能根据动作价值的后验概率，在每一步中选择最优动作。这种方法有时称为 “后验采样” 或 “Thompson采样”，其性能通常与本文中最好的方法（不需要先验分布）性能相近
贝叶斯方法甚至可以计算试探和开发间的最优平衡，虽然计算量会非常大，但是可以有效地近似，进而可以把赌博机问题转换为一种完整强化学习问题，这样就能使用 RL 方法求解，但这已经成为一个科研问题了，在此不做讨论。