补充知识----欧拉公式:
____________________________________________________________________________________________________________________________________
首先先给出一维离散傅里叶变换定义及求解:
已知离散数列
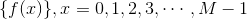
问题:是否存在离散数列
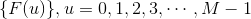
使得:
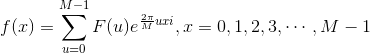
答案是肯定的。下面我们就来求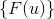
假设我们求该数列的第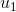
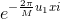
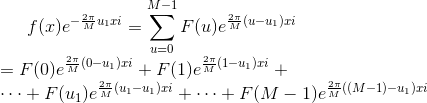
然后上式,我们两边对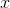
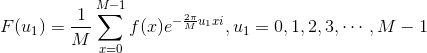
所以,我们找到了数列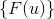
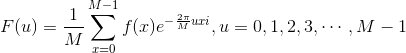
那么上式就称为:一维的离散的傅里叶变换。
—————————————————————————————————————————————————————————————————————————————
推广:二维离散的傅里叶变换:
已知离散的数列
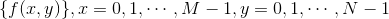
问题:是否存在数列
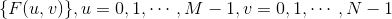
使得:

答案依然是肯定的,下面我们来求
假设我们求该数列的第

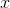
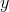
其中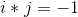
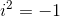
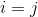
然后,我们称上式为二维离散的傅里叶变换。
————————————————————————————————————————————————————————————————————————————
关于傅里叶变换常用的一些术语:
傅里叶谱(幅度谱):
频率谱(功率谱):
相角:
其中: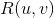
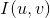
————————————————————————————————————————————————————————————————————————————
opencv中已经实现DFT,并有实例代码显示傅里叶谱,这里就不再啰嗦!







 本文详细解释了一维和二维离散傅里叶变换的定义与求解过程,包括变换公式推导和常见术语如傅里叶谱、幅度谱、功率谱、相角等概念。此外,还展示了如何在OpenCV中实现DFT及其应用实例。
本文详细解释了一维和二维离散傅里叶变换的定义与求解过程,包括变换公式推导和常见术语如傅里叶谱、幅度谱、功率谱、相角等概念。此外,还展示了如何在OpenCV中实现DFT及其应用实例。
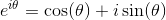
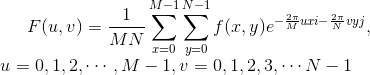
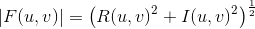
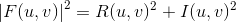
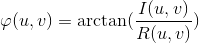
















 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








