Rongmao Chen, Yi Mu,
Senior Member, IEEE
, Guomin Yang,
Member, IEEE
, and Fuchun Guo
解决问题
为了实现加密文件的安全去重,Bellare等人在2013年的Eurocrypt上提出了一种新的密码学原语——消息锁定加密(MLE)。虽然可以通过扩展MLE方案来实现大文件的安全去重,但它需要终端用户和云服务器维护大量的元数据。这篇文章提出了一种新的方法来实现对大文件(加密)更有效的去重。所提出的方法称为块级消息锁定加密(BL-MLE),可以使用少量元数据集同时实现文件级和块级的去重、块密钥管理和所有权证明。同时,BL-MLE方案易于扩展以支持存储证明,从而适用于安全云存储。
贡献
1)提出了BL-MLE的形式化定义,双层去重、块密钥管理和所有权证明。安全模型还为每个功能单独定义,以获取明确的安全保证。
2)提出了一种具体的,易于修改以支持高效的存储证明的BL-MLE方案。,并且可以得到一个安全性更强的改进PoW协议,这使得我们的方案适用于安全云存储。
预备知识
猜测概率
给定一个具有最小熵的随机变量X, X的猜测概率为
。给定随机变量Y,具有条件最小熵
的随机变量X的条件猜测概率GP(X|Y)为
。
不可预测的块源
块源是一个多项式时间算法,它在输入
上返回
,其中M是
上的消息向量,
表示一些辅助信息。用
表示向量长度,即块的数量。对于所有的i ∈[1,n(λ)], M[i]表示消息M的第i个块。如果
可以忽略,则称M是一个不可预测的块源。
块级消息锁定加密
定义
语法:块级消息锁定加密方案由以下算法指定
Setup: 将安全参数λ作为输入,并返回系统参数P.
KeyGen:以公共参数P和文件消息M = M[1]||...||M[n]作为输入,并分别返回使用以下两个子算法生成的主密钥和块密钥
密钥生成算法:

![B-KeyGen(P,M[i])\rightarrow k_i](https://latex.csdn.net/eq?B-KeyGen%28P%2CM%5Bi%5D%29%5Crightarrow%20k_i)
加密算法:
![Enc(P,M[i],k_i)\rightarrow C[i]](https://latex.csdn.net/eq?Enc%28P%2CM%5Bi%5D%2Ck_i%29%5Crightarrow%20C%5Bi%5D)
解密算法:
![Dec(P,C[i],k_i)\rightarrow M[i]/ \bot](https://latex.csdn.net/eq?Dec%28P%2CC%5Bi%5D%2Ck_i%29%5Crightarrow%20M%5Bi%5D/%20%5Cbot)
标签生成算法:
![TagGen : F-TagGen(P,M)\rightarrow T_0 ; \ \ \ \ \ \ B-TagGen(P,M[i])\rightarrow T_i](https://latex.csdn.net/eq?TagGen%20%3A%20F-TagGen%28P%2CM%29%5Crightarrow%20T_0%20%3B%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20B-TagGen%28P%2CM%5Bi%5D%29%5Crightarrow%20T_i)
标签密文一致性检测:
![ConTest(T_i,C[i])\rightarrow True/False](https://latex.csdn.net/eq?ConTest%28T_i%2CC%5Bi%5D%29%5Crightarrow%20True/False) ;
;
(需要确保区块标识符(即区块标签)与上传的数据块实际上是一致的,以防止重复伪造攻击。)
标签验证算法:

密钥恢复算法:
![B-KeyRet(k_{mas},T_i,C[i])\rightarrow k_i/\bot](https://latex.csdn.net/eq?B-KeyRet%28k_%7Bmas%7D%2CT_i%2CC%5Bi%5D%29%5Crightarrow%20k_i/%5Cbot)
所有权证明生成算法:

所有权校验算法:

安全定义
如果在以下PRV$-CDA-B博弈中没有多项式时间对手a具有不可忽略的优势,那么在选择分布攻击下,BL-MLE方案是安全的:
Setup:敌手
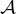 向挑战者发送不可预测的块源
向挑战者发送不可预测的块源
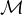 的描述。然后,挑战者生成系统参数
的描述。然后,挑战者生成系统参数
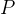 并向
并向
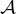 发送。
发送。
Challenge:挑战者挑选随机的 .如果
.如果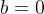 ,执行块源
,执行块源
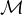 ,
,
 ,否则从
,否则从
 中均匀随机选择
中均匀随机选择
 .令
.令
 , 假设有
, 假设有
 个数据块,挑战者为每一个数据块生成密钥并生成密文C[i].最后生成文件标签和块标签。
个数据块,挑战者为每一个数据块生成密钥并生成密文C[i].最后生成文件标签和块标签。
![F-TagGen(P,M)\rightarrow T_0 ; \ \ \ \ \ \ B-TagGen(P,M[i])\rightarrow T_i](https://latex.csdn.net/eq?F-TagGen%28P%2CM%29%5Crightarrow%20T_0%20%3B%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20B-TagGen%28P%2CM%5Bi%5D%29%5Crightarrow%20T_i) 。 令
。 令
 ,最后,挑战者向对手提供辅助信息Z、标签T和密文C。
,最后,挑战者向对手提供辅助信息Z、标签T和密文C。
Output:收到(C,T,Z)之后,敌手输出他的猜测值b',如果b'=b就胜出。
文中将这样的对手
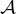 称为PRV$-CDA-B对手,并将对手
称为PRV$-CDA-B对手,并将对手
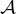 的优势定义为:
的优势定义为:
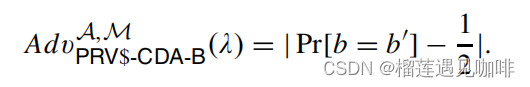
定义2:如果对于任意不可预测的块源
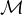 和任意多项式时间PRV$-CDA-B的敌手
和任意多项式时间PRV$-CDA-B的敌手
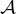 ,在选择分布攻击博弈
,在选择分布攻击博弈
 中优势可以忽略不计,则BL-MLE方案是安全的。
中优势可以忽略不计,则BL-MLE方案是安全的。
文中还定义了标签一致性,并设计了敌手的优势,感兴趣可以参看原文。
方案构造
设G, GT是两个相同素数阶p的乘法群,设g是G的生成元,I是GT的单位元。一个对称双线性映射e: G × G→GT,使得对于所有u,v∈G和A, b∈Zp。值得注意的是,e是可以有效计算的,并且e(g, g) ≠ I
Setup(
 ):输入
):输入
 ,生成素数p、两个p阶组群G,GT、G的生成器g和双线性映射e: G × G→GT。选择一个整数s∈N和三个散列函数
,生成素数p、两个p阶组群G,GT、G的生成器g和双线性映射e: G × G→GT。选择一个整数s∈N和三个散列函数 。随机选取s个元素
。随机选取s个元素 系统参数为
系统参数为
KeyGen(M)。给定一个数据文件M = M[1]||…||M[n] 其中对于所有1≤i≤n, M[i]∈{Zp}s,计算主键kmas和每个块键ki如下:
M-KeyGen(M): 以M为输入
k
mas
=
H
1
(
M
)
;
B-KeyGen(M[i
]
):
以
M
[
i
]为输入
, 输出
k
i =
H2(
M
[
i
]
)
.
Enc(
k
i
,
M[i])。以ki和M[i]为输入,输出![C[i]=H_3(k_i)\bigoplus M[i]](https://latex.csdn.net/eq?C%5Bi%5D%3DH_3%28k_i%29%5Cbigoplus%20M%5Bi%5D) .
.
Dec(
k
i
,
C[i
]). 给一个密文块和密钥作为输入,输出![M[i]=H_3(k_i)\bigoplus C[i]](https://latex.csdn.net/eq?M%5Bi%5D%3DH_3%28k_i%29%5Cbigoplus%20C%5Bi%5D) ,如果
,如果![k_i=H_2(M[i])](https://latex.csdn.net/eq?k_i%3DH_2%28M%5Bi%5D%29) ,输出M[i],否则输出错误。
,输出M[i],否则输出错误。
TagGen(M).
给每一个文件M生成文件标签T0和块标签Ti。
M-TagGen(M):
给M生成主密钥
 ,然后生成标签
,然后生成标签  .
.
B-TagGen(M
,
i
): 以M,块索引i为输入,生成主密钥,相关的块秘钥,块密文C[i],并将块密文分割成s个小的区块{![\left \{C[i][j] \right \}_{1\leq i \leq n}](https://latex.csdn.net/eq?%5Cleft%20%5C%7BC%5Bi%5D%5Bj%5D%20%5Cright%20%5C%7D_%7B1%5Cleq%20i%20%5Cleq%20n%7D) },输出
},输出![T_i=(k_i \prod \limits_{j=1}^s u_j^{C[i][j]})^{k_{mas}}](https://latex.csdn.net/eq?T_i%3D%28k_i%20%5Cprod%20%5Climits_%7Bj%3D1%7D%5Es%20u_j%5E%7BC%5Bi%5D%5Bj%5D%7D%29%5E%7Bk_%7Bmas%7D%7D) . 在生成块标签时,还生成了一些辅助数据auxi = e(ki, T0)并将其附加到块标签Ti上。
. 在生成块标签时,还生成了一些辅助数据auxi = e(ki, T0)并将其附加到块标签Ti上。
ConTest(
T
i
,
C
[i]). 给定一个块密文C[i]和带有辅助数据auxi的块标签Ti,将C[i]分成s个扇区:{C[i][j]}1≤j≤s。设T0为对应的文件标记。检查是否![e (T_i, g)\overset{\text{?}}{=} aux_i \cdot e ( \prod \limits_{j=1}^s u_j^{C[i][j] }, T_0).](https://latex.csdn.net/eq?e%20%28T_i%2C%20g%29%5Coverset%7B%5Ctext%7B%3F%7D%7D%7B%3D%7D%20aux_i%20%5Ccdot%20e%20%28%20%5Cprod%20%5Climits_%7Bj%3D1%7D%5Es%20u_j%5E%7BC%5Bi%5D%5Bj%5D%20%7D%2C%20T_0%29.) ,如果是,则输出1;否则,输出0。
,如果是,则输出1;否则,输出0。
EqTest(Ti, Ti', T0, T0').给定两个块标签Ti, Ti'和对应的文件标签T0, T0',检查是否 。如果是,输出1;否则,输出0。
。如果是,输出1;否则,输出0。

note:本文的安全性分析比较完备,我在进行安全性证明时主要参考本文。。此外,本文没有考虑完整性审计方面的内容。本文是块去重方向必须参考的一篇经典。
























 1399
1399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








