平衡二叉树（AVL）

一、 AVL树的定义

AVL树的名字来源于它的发明作者G.M. Adelson-Velsky 和 E.M. Landis。
AVL树是最先发明的自平衡二叉查找树（Self-Balancing Binary Search Tree,简称平衡二叉树）。
平衡二叉树定义(AVL)：它或者是一颗空树，或者具有以下性质的二叉排序树：它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。

• AVL树相较于二叉树，需要对每个节点跟踪一个**平衡因子（balance factor）**参数

• 平衡因子是根据节点的左右子树的高度来定义的，确切地说是：左子树高度—右子树高度

    	- 如果平衡因子大于0，称为左重
    	- 如果平衡因子小于0，称为右重
    	- 平衡因子等于0，则称为平衡
  

• 如果一个二叉树中每个节点的平衡因子都在-1，0，1之间，则把这个二叉树称为平衡树

• 在平衡树操作过程中（插入或删除），如果有节点的平衡因子超过了此范围，则需要一个重新平衡的过程。

二、插入操作

1.插入时平衡因子的变化

当在进行插入操作时：

1. 因为所有的新节点是作为叶节点插入树的，而新叶节点的平衡因子为零，所以我们对新插入的节点的平衡因子不作调整。

2. 但会影响其父节点的平衡因子

   	 - 作为左子节点插入，则父节点平衡因子会增加1
   	 - 作为右子节点插入，则父节点平衡因子会减少1
   

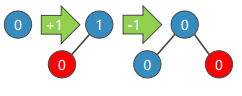
3. 这样的影响可能会随着其父节点到根节点的一直传递上去，直到：

		 - 	传递到根节点
		 -  某个父节点平衡因此被调整为0，不再影响上层节点的平衡因子

4. 代码如下：

    def _put(self, key, val, currentNode):
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                self._put(key, val, currentNode.leftChild)
            else:
                currentNode.leftChild = TreeNode(key, val, parent=currentNode)
                self.updateBalance(currentNode.leftChild)
        else:
            if currentNode.hasRightChild():
                self._put(key, val, currentNode.rightChild)
            else:
                currentNode.rightChild = TreeNode(key, val, parent=currentNode)
                self.updateBalance(currentNode.rightChild)
    def updateBalance(self, node):
        if node.balanceFactor > 1 or node.balanceFactor < -1:
            self.rebalance(node)
            return
        if node.parent != None:
        	#作为左子节点插入，则父节点平衡因子会增加1
            if node.isLeftChild():
                node.parent.balanceFactor += 1
            #作为右子节点插入，则父节点平衡因子会减少1
            elif node.isRightChild():
                node.parent.balanceFactor -= 1
            #如果父节点！=0 ，迭代，继续上传调整
            if node.parent.balanceFactor != 0:
                self.updateBalance(node.parent)

其中方法updateBalance，最核心的，与二叉树最大不同的就是rebalance，对节点进行了再平衡。

2. 树的再平衡

1. 进行平衡的规则

为了让 AVL 树恢复平衡，我们会在树上执行一个或多个“旋转”（rotation）。视左重或者右重进行旋转，同时更新相关父节点引用，更新旋转后被影响节点的平衡因子。其中有四种情况需要考虑。

• 左重右旋
• 左重且子树右重，需要先左旋，再右旋
• 右重左旋
  
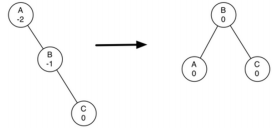
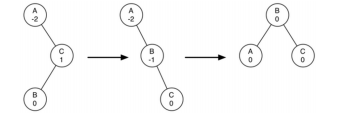
• 右重且子树左重，需要先右旋，再左旋
  

    def rebalance(self, node):
        if node.balanceFactor < 0:
            if node.rightChild.balanceFactor > 0:
                # Do an LR Rotation
                self.rotateRight(node.rightChild)
                self.rotateLeft(node)
            else:
                # single left
                self.rotateLeft(node)
        elif node.balanceFactor > 0:
            if node.leftChild.balanceFactor < 0:
                # Do an RL Rotation
                self.rotateLeft(node.leftChild)
                self.rotateRight(node)
            else:
                # single right
                self.rotateRight(node)

2.进行平衡时需要对树进行旋转，如何进行旋转
以右重为例：
一种情况：当newRoot没有左子节点

另一种情况：当newRoot有左子节点

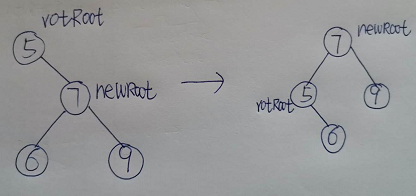
然后需要将对应的子节点，父节点都连接好就可以了

    def rotateLeft(self, rotRoot):
        newRoot = rotRoot.rightChild
        rotRoot.rightChild = newRoot.leftChild
        if newRoot.leftChild != None:
            newRoot.leftChild.parent = rotRoot
        newRoot.parent = rotRoot.parent
        if rotRoot.isRoot():
            self.root = newRoot
        else:
            if rotRoot.isLeftChild():
                rotRoot.parent.leftChild = newRoot
            else:
                rotRoot.parent.rightChild = newRoot
        newRoot.leftChild = rotRoot
        rotRoot.parent = newRoot
        rotRoot.balanceFactor = rotRoot.balanceFactor + 1 - min(newRoot.balanceFactor, 0)
        newRoot.balanceFactor = newRoot.balanceFactor + 1 + max(rotRoot.balanceFactor, 0)

三、 删除操作

1. 想要进行删除操作，首先需要在树中找到要删除的节点。

2. 平衡树在删除的时候有以下情况，但需要注意的是平衡因子的更新：

    1.当删除的节点（currentnode）是叶节点时，直接删除，对平衡因子进行更新
    2.当删除的节点有1个子节点时，有6种情况需要考虑（如下图所示），对平衡因子进行更新：
   

	 2.当删除的节点有两个子节点时，需要找到核实的节点来替代被删除的节点：
	 这个**后继节点**就是被删除节点的右子树中最小的那个。（它一定是个左子树，且再没有左子树）

在remove中最重要的是对平衡因子（balanceFactor）的更新

    def remove(self, currentNode):
        if currentNode.isLeaf():  # leaf
            if currentNode == currentNode.parent.leftChild:
            	#对平衡因子的更新，先更新，再修改，否则无法进行更新
                self.del_updateBalance(currentNode)
                currentNode.parent.leftChild = None
            else:
                self.del_updateBalance(currentNode)
                currentNode.parent.rightChild = None
        elif currentNode.hasBothChildren():  # interior
            succ = currentNode.findSuccessor()
            succ.spliceOut()
            currentNode.key = succ.key
            currentNode.payload = succ.payload
            self.del_updateBalance(currentNode)
        else:  # this node has one child
            if currentNode.hasLeftChild():
                if currentNode.isLeftChild():
                    currentNode.leftChild.parent = currentNode.parent
                    currentNode.parent.leftChild = currentNode.leftChild
                elif currentNode.isRightChild():
                    currentNode.leftChild.parent = currentNode.parent
                    currentNode.parent.rightChild = currentNode.leftChild
                else:
                    currentNode.replaceNodeData(currentNode