4邻接、8邻接、m邻接及像素的度量距离

Waygoer

于 2023-10-07 09:20:25 发布

阅读量1.8k

点赞数 4

分类专栏：数字图像处理文章标签：计算机视觉人工智能图像处理

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/wyr1849089774/article/details/133623378

版权

数字图像处理专栏收录该内容

5 篇文章 1 订阅

订阅专栏

数字图像处理中像素间的一些基本关系,在此做一下简要记录.

先引入几个邻域概念:

(1)位于坐标(x,y)处的像素p有4个水平和垂直的相邻像素,其坐标是

$\left ( x+1, y \right ) \left ( x-1,y \right )\left ( x,y+1 \right )\left ( x,y-1 \right )$

则这组像素称为p的4邻域,使用 $\mathbf{N_{4}\left ( p \right )}$ 表示.

(2)p的四个对角相邻像素的坐标是

$\left ( x+1, y+1 \right ) \left ( x+1,y-1 \right )\left ( x-1,y+1 \right )\left ( x-1,y-1 \right )$

用 $\mathbf{N_{D}\left ( p \right )}$ 表示.

(3) 以上所有的点并称为p的8邻域,用 $\mathbf{N_{8}\left ( p \right )}$ 表示.

先设定一个用于定义邻接性的灰度值集合,称为V.

在二值图像中,如果把具有1值的像素归诸于邻接像素,则V={1}.

在灰度图像中,该集合也是相同的概念,只不过V可以含有0~255的任意元素.

举个例子,V={14,37,247,255},说明这些灰度值的像素块可以来判断邻接性.

在接下来介绍时我们以二维图像为例来介绍邻接性.

4邻接

如果q在集合 $N_{4}\left ( p \right )$ 中,则具有V中数值的两个像素p和q是4邻接的.

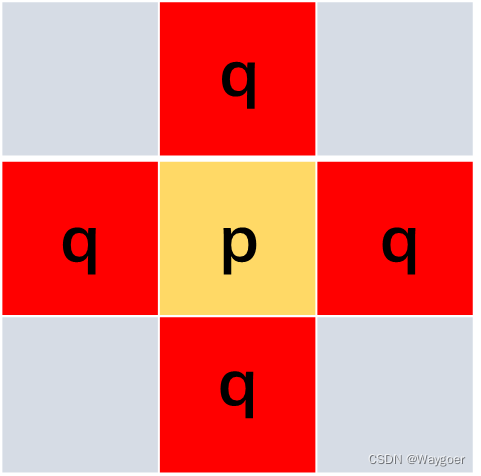
如上图所示,四周的四个红色像素块q均和p是四邻接的.

(特别注意,这是针对二维图像的情况,默认p和q都是1,若是灰度图像,还需要考虑p和q中的数值是否在V中!!! 以下例子都须注意该点,在之后不再重复说明)

8邻接

如果q在集合 $N_{8}\left ( p \right )$ 中,则具有V中数值的两个像素p和q是8邻接的.

如上图所示,四周的8个红色像素块q均和p是八邻接的.

特殊说明_8邻接的二义性

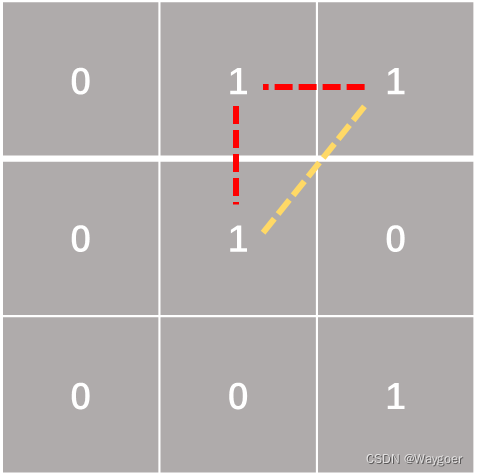
如上图所示,中间的"1"有两条路径(黄色路径&&红色路径)可到达右上角的"1" ,这就称作8邻接的二义性.在边缘检测时不希望出现这种二义性,故引入m邻接来消除采用8邻接时产生的二义性.

m邻接

如果

①q在 $N_{4}\left ( p \right )$ 中

或

②q在 $N_{D}\left ( p \right )$ 中,且集合 $N_{4}\left ( p \right )\bigcap N_{4}\left ( q \right )$ 中没有来自V中的数值的像素

则具有V中数值的两个像素p和q是m邻接的.

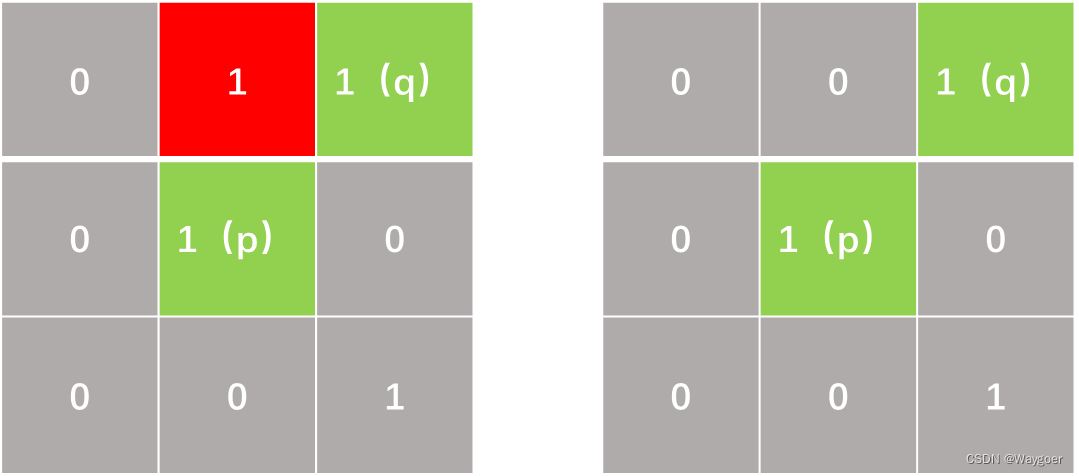
如下左图中p和q就不是m邻接,因为不满足集合 $N_{4}\left ( p \right )\bigcap N_{4}\left ( q \right )$ 中没有来自V中的数值的像素,也就是p和q除了直接连通外还有另一条折线路径可连通.

而如下右图中p和q就是m邻接的.

度量距离

定义：

对于坐标分别为 $\left ( x,y \right )\left ( s,t \right )\left ( v,w \right )$ 的像素p,q和z，如果

(a) $D\left ( p,q \right )\geqslant 0\left [ D\left ( p,q \right )= 0 \,while\,p = q\right ]$ (正定性）

(b) $D\left ( p,q \right ) = D\left ( q,p \right )$ (对称性）

(c) $D\left ( p,z \right ) \leqslant D\left ( p,q \right ) + D\left ( q,z \right )$ （距离三角不等式）

则 $D$ 是距离函数或度量。

以下介绍几个重点的距离定义——

①欧几里得（欧式）距离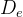 $D_{e}$

$D_{e}\left ( p,q \right ) = \left [ \left ( x-s \right )^{2} + \left ( y-t \right )^{2} \right ]^{1/2}$

对于欧式距离，距点 $\left ( x,y \right )$ 的距离小于等于某个值 $r$ 的像素，是中心在 $\left ( x,y \right )$ 且半径为 $r$ 的圆平面。

②城市街区距离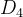 $D_{4}$

$D_{4}\left ( p,q \right ) = \left | x-s \right | + \left | y - t \right |$

对于城市街区距离，距点 $\left ( x,y \right )$ 的距离小于等于某个值 $r$ 的像素形成一个中心在 $(x,y)$ 的菱形，如下图所示。

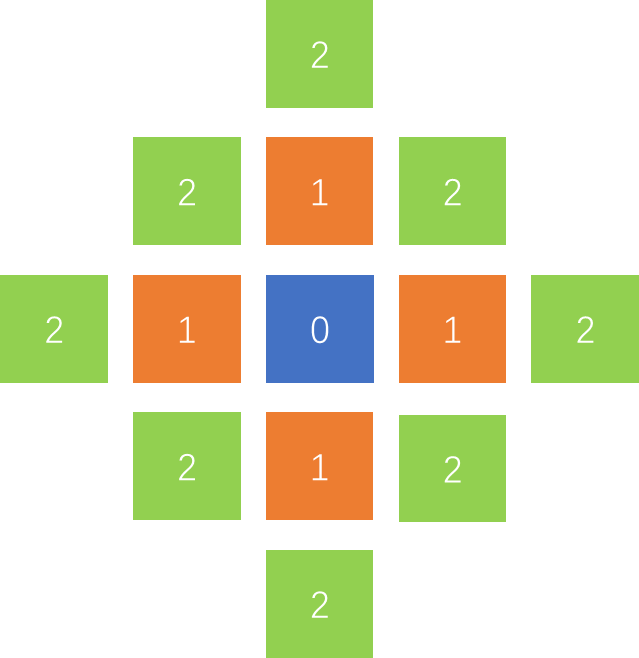
③棋盘距离 $D_{8}$

$D_{8}\left ( p,q \right ) = max(\left | x-s \right | , \left | y - t \right |)$

对于棋盘距离，距点 $\left ( x,y \right )$ 的距离小于等于某个值 $r$ 的像素形成一个中心在 $(x,y)$ 的方形，如下图所示。

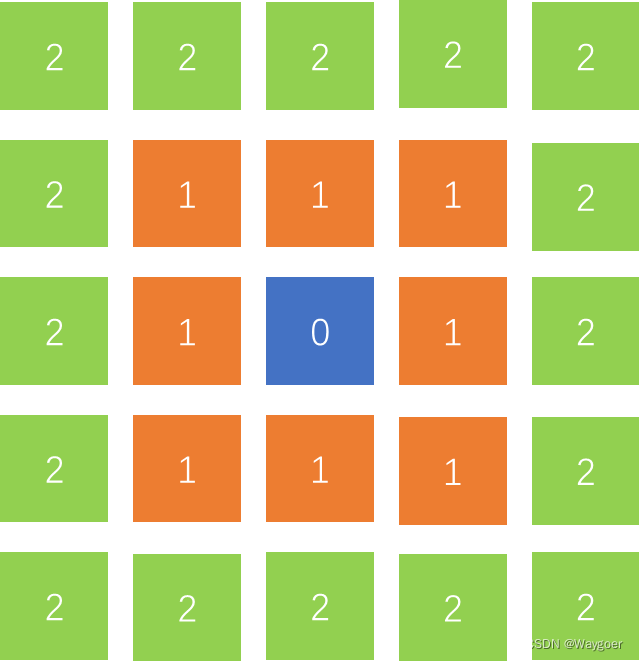
④m邻接距离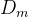 $D_{m}$

$D_{m}\left ( p, q \right ) =The\,shortest\,\,path\,\,between\,\,points\,\,\mathbf{p}\,\,and\,\,\boldsymbol{q}$

在此举例说明

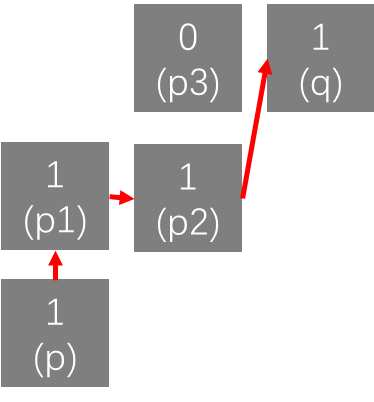
如上图所示，在这种情况下，p和p2就不是m邻接，所以p和q的m邻接距离

$D_{m}(p, q) = 3$

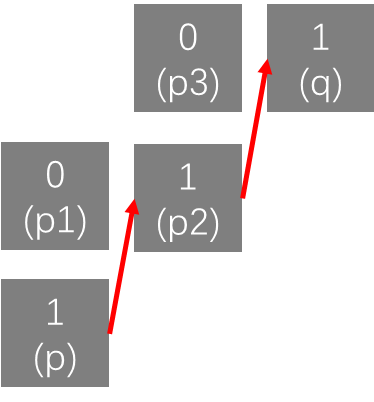
对于上图这种情况，p和p2是m邻接，p2和q也是m邻接，故p和q的m邻接距离

$D_{m}(p, q) = 2$

关注

4
点赞
踩
10

收藏

觉得还不错? 一键收藏
1
评论
4邻接、8邻接、m邻接及像素的度量距离

详细介绍数字图像处理中像素间的一些基本关系，包括4邻接、8邻接、m邻接、欧氏距离、城市街区距离、棋盘距离、m邻接距离等概念
复制链接

扫一扫

专栏目录

评论 1

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。