(6)与圆心相连的直线:给定一点p,其与圆心相连成的直线,会和圆有两个交点,如图。在上面定义的Point(点)类和Circle(圆)类基础上,设计一种方案,输出这两点的坐标。
提示:
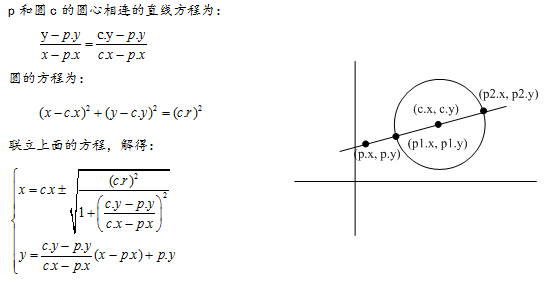
代码如下:

提示:

代码如下:
#include <iostream>
#include <Cmath>
using namespace std;
class Circle;
class Point
{
protected:
double x,y;
public:
Point(int xx=0,int yy=0):x(xx),y(yy) {}
friend ostream& operator<<(ostream&output,const Point &c);
friend void Point_intersection(Point &p,Circle &c,Point &p1,Point &p2); //求交点的友元函数
};
ostream& operator<<(ostream &output,const Point &c)
{
output<<"("<<c.x<<","<<c.y<<")"<<endl;
return output;
}
class Circle:public Point
{
protected:
double r;
public:
Circle(int xx=0,int yy=0,double rr=0):Point(xx,yy),r(rr){};
friend ostream& operator<<(ostream&output,const Circle &c);
friend void Point_intersection(Point &p,Circle &c,Point &p1,Point &p2); //求交点的友元函数
};
ostream& operator<<(ostream&output,const Circle &c)
{
output<<"("<<c.x<<","<<c.y<<","<<c.r<<")"<<endl;
return output;
}
void Point_intersection(Point &p,Circle &c,Point &p1,Point &p2)
{
p1.x=c.x+sqrt((c.r*c.r)/(1+((c.y-p.y)/(c.x-p.x)*(c.y-p.y)/(c.x-p.x))));
p2.x=c.x-sqrt((c.r*c.r)/(1+((c.y-p.y)/(c.x-p.x)*(c.y-p.y)/(c.x-p.x))));
p1.y=((c.y-p.y)/(c.x-p.x))*(p1.x-p.x)+p.y;
p2.y=((c.y-p.y)/(c.x-p.x))*(p2.x-p.x)+p.y;
}
int main( )
{
Circle c(3,2,4);
Point p(10,10),p1,p2;
Point_intersection(p,c,p1,p2);
cout<<"点p"<<p<<"与圆c"<<c<<"的圆心确定的一条直线与圆的两个交点:"<<endl;
cout<<"交点1: "<<p1<<endl;
cout<<"交点2: "<<p2<<endl;
return 0;
}

总结:
没有公式真心算不出来
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








