算法之路--前缀和与差分

茶馆大橘

已于 2023-03-10 17:30:26 修改

阅读量259

点赞数

文章标签：算法 Powered by 金山文档

于 2023-02-23 00:17:41 首次发布

本文链接：https://blog.csdn.net/wzc200406/article/details/129172292

版权

算法之路专栏收录该内容

7 篇文章 0 订阅

订阅专栏

一、学前缀和与差分有什么用？

多说无益，举个例子。

输入两个变量n,m。n表示数组长度，m表示对数组进行的操作次数。每次操作需要输入两个数l，r。现在需要你求出区间【l，r】之间的元素之和。

你可能立马就有思路了：不是很简单吗？我直接for循环暴力求解不就行了。

于是你大概会写出以下代码

const int N = 100010;
int a[N];
int n,m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
while(m--)
{
    int l, r;
    int ans = 0;
    scanf("%d%d", &l, &r);
    for(int i = l; i <= r; i++)
    { 
        ans += a[i];
    }
    printf("%d\n",sum);
}

咦，好像很对哦！那如果我再加上一个条件呢？

0<=n,m<=1000000

你会发现，好像数据稍微大一点，就会超时。这是因为上述的算法的时间复杂度大约为O（n*m）

如果你学习了前缀和就不会发生以上情况，因为前缀和的时间复杂度可以降至O（n+m）

所以，说白了，前缀和算法就是一种可以快速求出区间【j，r】的数值之和的小技巧，差分则可以看作是前缀和的一种逆运算。两者的合理运用，可以提高复杂问题的解决效率，使得问题变得简单。

二、前缀和

前缀和算法就是一种可以快速求出区间【j，r】的数值之和的小技巧，有一维和二维之分，对应的是一维数组问题以及稍微复杂的二维矩阵问题。

一维前缀和

【基本原理】 Si=a1+a2+...+ai; S[r]-S[l-1];

求【l，r】间元素 al+...+ar

S(l-1) = a1 + a2 + ... + a(l-1) ; (1)

S(r)= a1 + a2 + ... + a(l-1) + al + ... + ar; (2)

(2)-(1)即可

【练习理解】

  输入两个变量n,m。n表示数组长度，m表示对数组进行的操作次数。每次操作需要输入两个数l，r。现在需要你求出区间【l，r】之间的元素之和。

#include <iostream>
using namespace std;
const int N = 10010;
int n, m;
int a[N], sun[N];
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

    for (int i = 1; i <= n; i ++ ) sum[i] = sum[i - 1] + a[i]; // 精髓就在这，提前初始化好前缀和数组

    while (m -- )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", sum[r] - sum[l - 1]); // 区间和的计算
    }

    return 0;
}

for (int i = 1; i <= n; i ++ ) sum[i] = sum[i - 1] + a[i];

这句话就是这个算法的核心了。思路就是提前将前缀和数组初始化好，就不用再循环反复，直接可以利用

printf("%d\n", sum[r] - sum[l - 1]);

二维前缀和

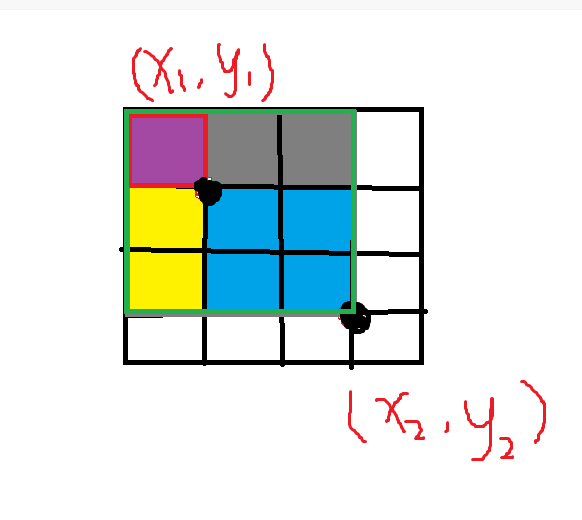
【例题】输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

即求出下图蓝色区域的数值之和

【基本思路】

首先，明白什么是二维矩阵的前缀和。如图所示，点（X1，Y1）的前缀和为红色边框的数值。点（X2，Y2）的前缀和为绿色边框的数值。（我们当作面积讨论）

为什么要加回一个红色框的面积呢？因为减去黄色面积和灰色面积时，将红色面积重复减了两次，所以要加回来。这样一来，我们解决了如何求（X1，Y1）和（X2，Y2）间的面积问题，但是我们要如何求出S【i,j】来解决问题呢？

按照刚才的求面积的思路，如下图所示

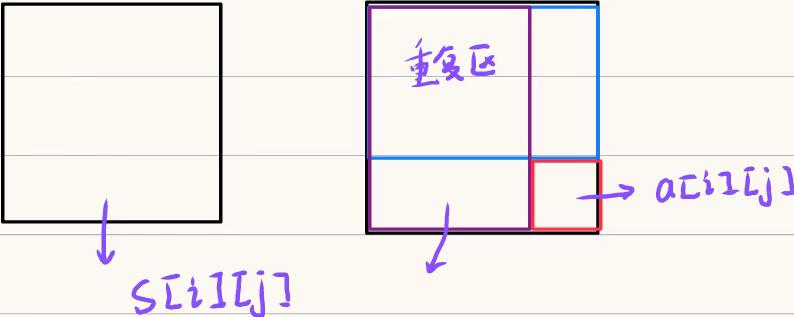
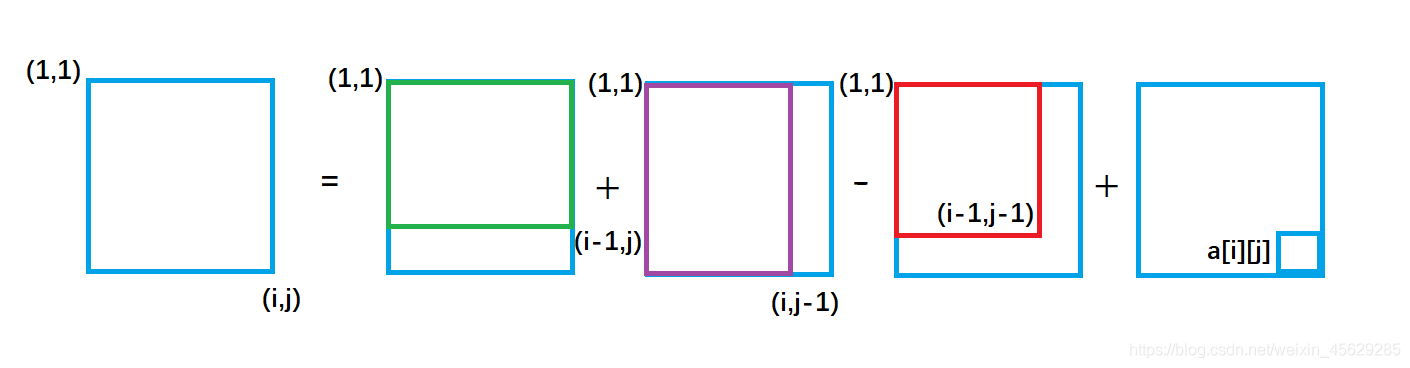
还是一样的，左上角有一个重复区我们减了两遍，需要加回来。

那么，我们就可以根据以上原理写出以下规律

如何求（X1，Y1）和（X2，Y2）间的面积？

S【x2,y2】-S【x1-1,y2】-S【X2,y1-1】+S【x1-1,y1-1】

如何求出S【i,j】

S【】=S【i；j-1】+S【i-1，j】-S【i-1，j-1】+a【i，j】

【代码实现】

【例题】输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。

#include <iostream>
using namespace std;
const int N = 1001;
int n, m, q;
int s[N][N];
int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &s[i][j]);
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]; //初始化前缀和数组
    while (q -- )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}