函数的最佳逼近问题：最小二乘法

1. 最佳逼近问题

\qquad 简单来说，最佳逼近问题就是用一些 (基)函数 φ i ( x ) , i ∈ { 0 , 1 , ⋯   , M } \varphi_{i}(\boldsymbol x),i\in \{0,1,\cdots,M\} φi​(x),i∈{0,1,⋯,M} 的线性组合来逼近某个函数 $f(\mathbf{x})$，也就是定义

\qquad\qquad $\phi (\mathbf{x})=\sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x})=a_0{\phi }_0(\mathbf{x})+a_1{\phi }_1(\mathbf{x})+\cdots +a_M{\phi }_M(\mathbf{x})$

\qquad 使得 $f(\mathbf{x})$ 和 $\phi (\mathbf{x})$ 在某种(度量)意义下最小，常见的度量包括 ${\ell }_1$ 范数，${\ell }_2$ 范数（最佳平方逼近），${\ell }_{\infty }$ 范数（最佳一致逼近）。

\qquad 例如，多项式曲线拟合的基函数可以定义为 ${\phi }_n(x)=x^n$，就有

\qquad\qquad $\phi (x)=\sum _{n=0}^M{a}_n{\phi }_n(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_M{x}^M$

\qquad 当 $f(x)$ 具有周期性质，可以采用三角多项式来逼近，就有

\qquad\qquad $\phi (x)=a_0+a_1\cos x+b_1\sin x+\cdots +a_M\cos (Mx)+b_M\sin (Mx)$

\qquad 若基函数具有正交性，则会大大简化最佳逼近问题。
\qquad

2. 最佳平方(最小二乘)逼近

\qquad 最佳平方逼近采用 ${\ell }_2$ 范数来度量 $f(\mathbf{x})$ 和 $\phi (\mathbf{x})$ 之间接近程度。

\qquad 函数 $f(\mathbf{x})$ 的最佳逼近 ${\phi }^{\ast }(\mathbf{x})$ 满足：

\qquad\qquad $\parallel f(\mathbf{x})-{\phi }^{\ast }(\mathbf{x}){\parallel }_2^2=\min \parallel f(\mathbf{x})-\phi (\mathbf{x}){\parallel }_2^2$

\qquad 因此，可定义误差函数 $E(a_0,\cdots ,a_M)$ 为：

\qquad\qquad $\begin{array}{rl}E(a_0,\cdots ,a_M)& =\parallel f(\mathbf{x})-\phi (\mathbf{x}){\parallel }_2^2\\ & =\parallel f(\mathbf{x})-\sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x}){\parallel }_2^2\\ & =\int [f(\mathbf{x})-\sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x}){]}^{2}dx\end{array}$

\qquad 此时，误差函数 $E(a_0,\cdots ,a_M)$ 为系数 $(a_0,\cdots ,a_M)$ 的二次函数，其取极值的必要条件为：

\qquad\qquad $\begin{array}{rl}\frac{\partial E(a_0,\cdots ,a_M)}{\partial a_k}& =0(k=0,1,\cdots ,M)\end{array}$

\qquad 因此

\qquad\qquad $\begin{array}{rl}\frac{\partial E(a_0,\cdots ,a_M)}{\partial a_k}& =-2\int [f(\mathbf{x})-\sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x})]{\phi }_k(\mathbf{x})dx\\ & =0(k=0,1,\cdots ,M)\end{array}$

\qquad 于是

\qquad\qquad $\begin{array}{rl}\int f(\mathbf{x}){\phi }_k(\mathbf{x})dx& =\int \sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x}){\phi }_k(\mathbf{x})dx\\ & =\sum _{n=0}^M{a}_n\int {\phi }_n(\mathbf{x}){\phi }_k(\mathbf{x})dx\end{array}$

\qquad 写成函数内积的形式：

\qquad\qquad $(f,{\phi }_k)=\sum _{n=0}^M{a}_n({\phi }_n,{\phi }_k)$

\qquad 实际上是一个关于 $a_0,\cdots ,a_M$ 的线性方程组，称为法方程$\text{(normal equation)}$：
\qquad

\qquad\qquad $\left[\begin{array}{cccc}({\phi }_0,{\phi }_0)& ({\phi }_1,{\phi }_0)& \cdots & ({\phi }_M,{\phi }_0)\\ ({\phi }_0,{\phi }_1)& ({\phi }_1,{\phi }_1)& \cdots & ({\phi }_M,{\phi }_1)\\ ⋮& ⋮& ⋮& ⋮\\ ({\phi }_0,{\phi }_M)& ({\phi }_1,{\phi }_M)& \cdots & ({\phi }_M,{\phi }_M)\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ ⋮\\ a_M\end{array}\right]=\left[\begin{array}{c}(f,{\phi }_0)\\ (f,{\phi }_1)\\ ⋮\\ (f,{\phi }_M)\end{array}\right](1)$

\qquad
\qquad 求解该线性方程组，就可以得到系数 $(a_0,\cdots ,a_M)$ 的值。

\qquad 对于连续函数的内积，通常有：

\qquad\qquad $(f,{\phi }_k)={\int }_a^{b}f(x){\phi }_k(x)dx$

\qquad 以及

\qquad\qquad $({\phi }_n,{\phi }_k)={\int }_a^b{\phi }_n(x){\phi }_k(x)dx$

\qquad

离散情况——以线性回归为例

\qquad 离散情况时，以一维线性回归为例，已知观测样本集 { x i , y i } ∣ 0 N \{x_{i},y_{i}\}\big|_{0}^{N} {xi​,yi​}∣ ∣​0N​，要求出函数 $f(x)$ 的逼近函数：

$\phi (x)=\sum _{n=0}^1{a}_n{\phi }_n(x)=a_0+a_{1}x$
\qquad
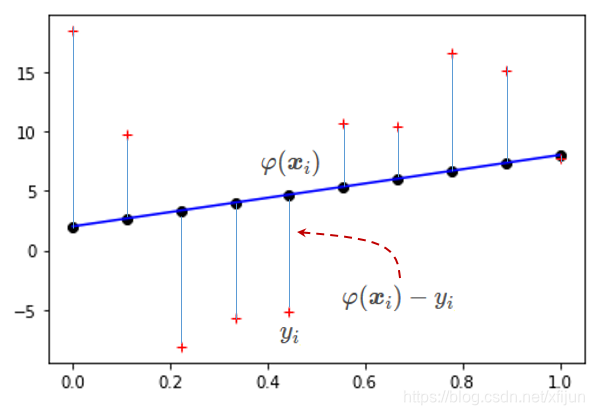
\qquad 上图中，线性回归关于每个观测点 $(x_i,y_i)$ 的 ${\ell }_2$ 损失（平方误差）为：$[\phi (x_i)-y_i{]}^2$

\qquad 误差函数定义为“误差的平方之和”：

\qquad\qquad $\begin{array}{rl}E(a_0,a_1)& =[\phi (x_0)-y_0{]}^2+[\phi (x_1)-y_1{]}^2+\cdots +[\phi (x_N)-y_N{]}^2\\ & =\sum _{i=0}^N[\phi (x_i)-y_i{]}^2\\ & =\sum _{i=0}^N(y_i-a_0-a_1{x}_i{)}^2\end{array}$

\qquad 通过求出系数 $(a_0,a_1)$ 的值，用 $\phi (x)\approx f(x)$。

• 对误差函数求 $a_0$ 的偏导：

$\frac{\partial E(a_0,a_1)}{\partial a_0}=2\sum _{i=0}^N(y_i-a_0-a_1{x}_i)(-1)=0$

\qquad\qquad 可以写成：$a_0\sum _{i=0}^{N}1+a_1\sum _{i=0}^N{x}_i=\sum _{i=0}^N{y}_i$

$⟹$$a_0=\frac{1}{N}\sum _{i=0}^N(y_i-a_1{x}_i)$

• 对误差函数求 $a_1$ 的偏导：

$\frac{\partial E(a_0,a_1)}{\partial a_1}=2\sum _{i=0}^N(y_i-a_0-a_1{x}_i)(-x_i)=0$

\qquad\qquad 可以写成：$a_0\sum _{i=0}^N{x}_i+a_1\sum _{i=0}^N{x}_i^2=\sum _{i=0}^N{y}_i{x}_i$

$⟹$$a_1=\frac{\sum _{i=0}^N(y_i-a_0)x_i}{\sum _{i=0}^N{x}_i^2}$

\qquad\qquad 代入 $a_0$，可得到：$a_1=\frac{\sum _{i=0}^N{y}_i\left(x_i-\frac{1}{N}\sum _{i=0}^N{x}_i\right)}{\sum _{i=0}^N{x}_i^2-\frac{1}{N}{\left(\sum _{i=0}^N{x}_i\right)}^2}$

\qquad\qquad 若记样本的均值为 $\bar{x}=\frac{1}{N}\sum _{i=0}^N{x}_i$，则$a_1=\frac{\sum _{i=0}^N{y}_i\left(x_i-\bar{x}\right)}{\sum _{i=0}^N{x}_i^2-N{\bar{x}}^2}$

\qquad 这种求解，实际上就是求4.1节中的解线性方程组 $(1)$ 的过程。
\qquad

3. 最小二乘学习(离散情况的另一种描述)

\qquad 如下图所示，已知观测样本集 { x i , y i } ∣ 0 N \{\boldsymbol x_{i},y_{i}\}\big|_{0}^{N} {xi​,yi​}∣ ∣​0N​，仍然采用线性模型：

\qquad\qquad $\begin{array}{rl}\phi (\mathbf{x})& =\sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x})\\ & =a_0{\phi }_0(\mathbf{x})+a_1{\phi }_1(\mathbf{x})+\cdots +a_M{\phi }_M(\mathbf{x})\\ & ={\mathbf{\theta }}^T\mathbf{\varphi }(\mathbf{x})={\mathbf{\varphi }}^T(\mathbf{x})\mathbf{\theta }\end{array}$

\qquad 其中，$\mathbf{\theta }=[a_0,a_1,\cdots ,a_M{]}^T$，
\qquad 　　　$\mathbf{\varphi }(\mathbf{x})=[{\phi }_0(\mathbf{x}),{\phi }_1(\mathbf{x}),\cdots ,{\phi }_M(\mathbf{x}){]}^T$

\qquad
\qquad 上图中，线性模型关于每个观测点 $({\mathbf{x}}_i,y_i)$ 的 ${\ell }_2$ 损失（平方误差）为：$[\phi ({\mathbf{x}}_i)-y_i{]}^2$

\qquad 将“数据集所有观测点上的平方误差之和”设为损失函数 $\text{(loss function)}$：

\qquad\qquad $\begin{array}{rl}J(\mathbf{\theta })& =[\phi ({\mathbf{x}}_0)-y_0{]}^2+[\phi ({\mathbf{x}}_1)-y_1{]}^2+\cdots +[\phi ({\mathbf{x}}_N)-y_N{]}^2\\ & =\sum _{i=0}^N[\phi ({\mathbf{x}}_i)-y_i{]}^2\\ & =\sum _{i=0}^N[{\mathbf{\theta }}^T\mathbf{\varphi }({\mathbf{x}}_i)-y_i{]}^2\\ & =\parallel \Phi \mathbf{\theta }-\mathbf{y}{\parallel }_2^2\end{array}$

\qquad 其中，$\mathbf{y}=[y_0,y_1,\cdots ,y_N{]}^T$

\qquad 　　　$\Phi =\left[\begin{array}{c}\mathbf{\varphi }({\mathbf{x}}_0{)}^T\\ \mathbf{\varphi }({\mathbf{x}}_1{)}^T\\ ⋮\\ \mathbf{\varphi }({\mathbf{x}}_N{)}^T\end{array}\right]=\left[\begin{array}{cccc}{\phi }_0({\mathbf{x}}_0)& {\phi }_1({\mathbf{x}}_0)& \cdots & {\phi }_M({\mathbf{x}}_0)\\ {\phi }_0({\mathbf{x}}_1)& {\phi }_1({\mathbf{x}}_1)& \cdots & {\phi }_M({\mathbf{x}}_1)\\ ⋮& ⋮& & ⋮\\ {\phi }_0({\mathbf{x}}_N)& {\phi }_1({\mathbf{x}}_N)& \cdots & {\phi }_M({\mathbf{x}}_N)\end{array}\right]$

\qquad
\qquad\qquad 这里的 $\Phi$ 称为设计矩阵$\text{(design matrix)}$，其元素为 ${\Phi }_{nm}={\phi }_m({\mathbf{x}}_n)$
\qquad
\qquad 损失函数 $J(\mathbf{\theta })$ 对系数 $\mathbf{\theta }$ 求偏导：

\qquad\qquad $\begin{array}{rl}\frac{\partial J(\mathbf{\theta })}{\partial \mathbf{\theta }}& =2{\Phi }^T(\Phi \mathbf{\theta }-\mathbf{y})=0\end{array}$

\qquad 可得到：

\qquad\qquad ${\Phi }^T\Phi \mathbf{\theta }={\Phi }^T\mathbf{y}(2)$

\qquad 显然，线性方程组（2）和（1）是等价的，可求得：

\qquad\qquad $\mathbf{\theta }=({\Phi }^T\Phi {)}^{-1}{\Phi }^T\mathbf{y}(3)$

线性方程组（1）和（2）的左端系数矩阵 ${\Phi }^T\Phi$ 存在是否可逆的问题，最小二乘解（3）是线性方程组（2）的解析解
在 ${\Phi }^T\Phi$ 不可逆或者观测数据集非常庞大的时候，求解析解的方式难以实现，需要采用梯度下降法之类的最优化算法来求取近似解

\qquad

最小二乘解的几何意义

\qquad 最小二乘解的几何意义如下图描述：

From 《PRML》Fig 3.2

\qquad 考虑线性方程组 $\Phi \mathbf{\theta }-\mathbf{y}=0$，可表示为：

\qquad\qquad $[{\mathbf{\phi }}_0,{\mathbf{\phi }}_1,{\mathbf{\phi }}_2,\cdots ,{\mathbf{\phi }}_M]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_M\end{array}\right]=\mathbf{y}$

\qquad 其中，${\mathbf{\phi }}_i=[{\phi }_i({\mathbf{x}}_0),{\phi }_i({\mathbf{x}}_1),{\phi }_i({\mathbf{x}}_2),\cdots ,{\phi }_i({\mathbf{x}}_N){]}^T$
\qquad 　　　$\mathbf{y}=[y_0,y_1,y_2,\cdots ,y_N{]}^T$

\qquad 图中的 $\mathcal{S}=C(\Phi )$，表示矩阵 $\Phi =[{\mathbf{\phi }}_0,{\mathbf{\phi }}_1,{\mathbf{\phi }}_2,\cdots ,{\mathbf{\phi }}_M]$ 的列空间$\text{(column space)}$。

• 如果 $\mathbf{y}\in \mathcal{S}$，线性方程组 $\Phi \mathbf{\theta }=\mathbf{y}$ 有唯一解
• 如果 $\mathbf{y}\notin \mathcal{S}$，线性方程组 $\Phi \mathbf{\theta }=\mathbf{y}$ 无解，只能到 $\mathcal{S}$ 中找一个最接近 $\mathbf{y}$ 的解，最小二乘解是指图中的 $\hat{\mathbf{y}}$（在${\ell }_2$ 范数下 $\parallel \mathbf{y}-\hat{\mathbf{y}}{\parallel }_2^2$　的值最小，$\hat{\mathbf{y}}\in \mathcal{S}$）

4. 最小二乘法实现曲线拟合

4.1 线性回归(解方程组1)

\qquad 以比较简单的曲线拟合问题为例，如果我们对于函数 $f(x)$ 的了解只有一个观测样本集 $\{(x_i,y_i)\}{|}_0^N$，如下图中绿色的 ‘+’ 所标记的这些数据点所示。

图1线性函数

\qquad 曲线拟合的目标是：基于这些观测数据 { x i , y i } ∣ 0 N \{x_{i},y_{i}\}\big|_{0}^{N} {xi​,yi​}∣ ∣​0N​，用最佳平方逼近的方式来估计真实函数 $f(x)$ 的表达式，观测值满足 $y_i=f(x_i)+{\epsilon }_i$。

\qquad 令基函数为 ${\phi }_n(x)=x^n$，则多项式函数逼近为：

\qquad\qquad $\phi (x)=\sum _{n=0}^M{a}_n{\phi }_n(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_M{x}^M$

\qquad 通过求出系数 $(a_0,\cdots ,a_M)$ 的值，用 $\phi (x)\approx f(x)$，实际上就是计算：$(f,{\phi }_k)=\sum _{n=0}^M{a}_n({\phi }_n,{\phi }_k)$

\qquad 曲线拟合问题描述的是离散的情况。考虑图1中的线性拟合问题，只需要计算两个系数 $a_0$ 和 $a_1$，近似函数 $\phi (x)=a_0{\phi }_0(x)+a_1{\phi }_1(x)=a_0+a_{1}x$。

\qquad 也就是计算线性方程组的未知数 $a_0$ 和 $a_1$：

\qquad\qquad $\left[\begin{array}{cc}({\phi }_0,{\phi }_0)& ({\phi }_1,{\phi }_0)\\ ({\phi }_0,{\phi }_1)& ({\phi }_1,{\phi }_1)\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\end{array}\right]=\left[\begin{array}{c}(f,{\phi }_0)\\ (f,{\phi }_1)\end{array}\right]$

\qquad 其中，${\phi }_0(x)=1$，${\phi }_1(x)=x$。

\qquad 对于观测样本集 $\{(x_i,y_i)\}{|}_0^N$，离散形式的内积为：

\qquad\qquad $(f,{\phi }_k)=\sum _{i=0}^N{y}_i{\phi }_k(x_i)=\{\begin{array}{ll}\sum _{i=0}^N{y}_i& (k=0)\\ \sum _{i=0}^N{y}_i{x}_i& (k=1)\end{array}$

\qquad\qquad $({\phi }_n,{\phi }_k)=\sum _{i=0}^N{\phi }_n(x_i){\phi }_k(x_i)=\{\begin{array}{cc}\sum _{i=0}^{N}1& (n=0,k=0)\\ \sum _{i=0}^N{x}_i& (n=0,k=1)\\ \sum _{i=0}^N{x}_i& (n=1,k=0)\\ \sum _{i=0}^N{x}_i^2& (n=1,k=1)\end{array}$

\qquad 因此，线性方程组为（和第2节中的过程一样）：

\qquad\qquad $\left[\begin{array}{cc}\sum _{i=0}^{N}1& \sum _{i=0}^N{x}_i\\ \sum _{i=0}^N{x}_i& \sum _{i=0}^N{x}_i^2\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\end{array}\right]=\left[\begin{array}{c}\sum _{i=0}^N{y}_i\\ \sum _{i=0}^N{y}_i{x}_i\end{array}\right]$

代码实现

import numpy as np
import matplotlib.pyplot as plt

def gen_lineardata(a,b,x):
    y = a*x + b
    y_noise = y + np.random.randn(len(x))*30
    return y, y_noise

def linear_regression(y_noise,x):
    a11 = len(x)
    a12 = np.sum(x)
    a22 = np.sum(np.power(x,2))
    f1 = np.sum(y_noise)
    f2 = np.sum(y_noise*x)
    coef = np.dot(np.linalg.inv(np.array([[a11,a12],[a12,a22]])),np.array([f1,f2]))
    return coef


if __name__ == '__main__':
    x = np.linspace(0,20,200)
    a = int(np.random.rand()*10)+1
    b = int(np.random.rand()*20)+1
    y, y_noise = gen_lineardata(a,b,x)
    plt.plot(x,y,'b')
    plt.plot(x,y_noise,'g+')
    
    coef = linear_regression(y_noise,x)
    a1 = coef[1]
    b1 = coef[0]
    print(coef)
    y1,y2 = gen_lineardata(a1,b1,x)
    plt.plot(x,y1,'r')
    plt.legend(labels=['original data','noise data','least-squares'],loc='upper left')
    plt.title('y='+str(a)+'x +'+str(b))
    plt.show()

某一次的实现结果：b=11.38812346, a=6.59033571（真实值为b=10,a=7）

\qquad 线性回归的实现也可以采用解方程组（2）的方式（M=1）：

def linear_regression_approx(y_noise,x,M):
    design_matrix = np.asmatrix(np.ones(len(x))).T
    for i in range(1,M+1):
        arr = np.asmatrix(np.power(x,i)).T
        design_matrix  = np.concatenate((design_matrix ,arr),axis=1)
    
    coef = (design_matrix.T*design_matrix).I*(design_matrix.T*(np.asmatrix(y_noise).T))
    
    return np.asarray(coef)

\quad

4.2 梯度下降法实现线性回归

梯度下降法：

1. 求误差函数 $E(\mathbf{w})$ 关于参数 $\mathbf{w}$ 的梯度 ${\nabla }_{\mathbf{w}}E(\mathbf{w})$

\qquad 考虑训练集 { x i , y i } i = 0 N − 1 \{x_i, y_i\}_{i=0}^{N-1} {xi​,yi​}i=0N−1​上的线性回归问题：

$(1)$ 假设回归函数为 $y=w_{0}x+w_1,\mathbf{w}=[w_0,w_1{]}^T$
$(2)$ 目标向量为 $\mathbf{Y}=[y_0,y_1,\cdots ,y_{N-1}{]}^T$，输入样本为 $\mathbf{X}={\left[\begin{array}{cccc}{x}_0& x_1& \cdots & x_{N-1}\\ 1& 1& \cdots & 1\end{array}\right]}^T$

$(3)$ 误差函数为 $E(\mathbf{w})=\frac{1}{N}\parallel \mathbf{Y}-\mathbf{X}\mathbf{w}{\parallel }_2^2=\frac{1}{N}(\mathbf{Y}-\mathbf{X}\mathbf{w}{)}^T(\mathbf{Y}-\mathbf{X}\mathbf{w})$

\qquad 可求得：
$\begin{array}{rl}{\nabla }_{\mathbf{w}}E(\mathbf{w})& =\frac{1}{N}(-2{\mathbf{X}}^T\mathbf{Y}+2{\mathbf{X}}^T\mathbf{X}\mathbf{w})\\ & =-\frac{2}{N}{\mathbf{X}}^T(\mathbf{Y}-\mathbf{X}\mathbf{w})\end{array}$

2. 更新参数 ${\mathbf{w}}^{(k+1)}={\mathbf{w}}^{(k)}-\eta {\nabla }_{\mathbf{w}}E(\mathbf{w})$，其中 $\eta$ 为学习率

\qquad 因此，权向量的更新公式为：

${\mathbf{w}}^{(k+1)}={\mathbf{w}}^{(k)}+\eta \frac{2}{N}{X}^T(\mathbf{Y}-\mathbf{X}\mathbf{w})$

实现代码：

import numpy as np
import matplotlib.pyplot as plt
def gen_lineardata(a,b,x):
    y = a*x + b
    y_noise = y + np.random.randn(len(x))*30
    return y, y_noise
def linear_regression_approx(y_noise,x,M):
    design_matrix = np.asmatrix(np.ones(len(x))).T
    for i in range(1,M+1):
        arr = np.asmatrix(np.power(x,i)).T
        design_matrix  = np.concatenate((design_matrix ,arr),axis=1)    
    coef = (design_matrix.T*design_matrix).I*(design_matrix.T*(np.asmatrix(y_noise).T))    
    return np.asarray(coef)
def Gradient_descent(y_noise,x,eta=0.001): #学习率过大会导致求解过程无法收敛
    w0 = np.random.randn(2,1)
    num = len(x)
    xhat = np.concatenate((x.reshape(-1,1),np.ones((num,1))), axis=1)
    while True:        
        err = 2*(y_noise.reshape(-1,1) - xhat.dot(w0))/num
    #    print(np.sum(np.abs(err)))
        w1 = w0 + eta*np.dot(xhat.T, err)
        if np.sum(np.abs(w1-w0))<0.00001:
            break
        w0 = w1.copy()
    return  w1
if __name__ == '__main__':
    x = np.linspace(0,20,200)
    a = int(np.random.rand()*10)+1
    b = int(np.random.rand()*20)+1
    y, y_noise = gen_lineardata(a,b,x)    
    plt.plot(x,y_noise,'g.')    
    coef1 = linear_regression_approx(y_noise,x,1)
    print(coef1)
    a1 = coef1[1]
    b1 = coef1[0]
    y1,y2 = gen_lineardata(a1,b1,x)
    plt.plot(x,y1,'r')
    coef2 = Gradient_descent(y_noise,x)
    print(coef2)
    a1 = coef2[0]
    b1 = coef2[1]
    y1,y2 = gen_lineardata(a1,b1,x)
    plt.plot(x,y1,'k')
    plt.legend(labels=['noise data','linear regressor','gradient descent'],loc='upper left')
    plt.title('y='+str(a)+'x +'+str(b))
    plt.show()

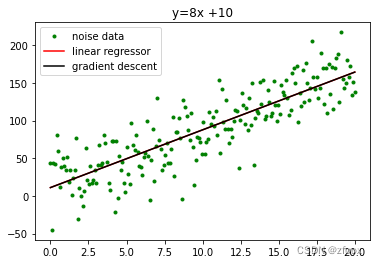
运行结果为
coef1: [[11.01307632]
　　　 [ 7.66747285]]　　　　　　 梯度下降法
coef2: [[ 7.66886398]
　　　 [10.99451616]]　　　　　　公式（3）的解析解
　　　

\qquad

4.3 周期函数的逼近(解方程组2)

\qquad 针对具有周期性质的数据集，更适合采用三角函数作为基函数，即采用公式：

\qquad\qquad $\phi (x)=a_0+a_1\cos x+b_1\sin x+\cdots +a_M\cos (Mx)+b_M\sin (Mx)$

\qquad 根据公式（3）求出系数。

import numpy as np
import matplotlib.pyplot as plt

def gen_data(x):
    y = 2*np.sin(2*np.pi*x) + 3*np.cos(3*np.pi*x)
    y_noise = y + np.random.randn(len(x))
    return y, y_noise

def least_squares_approx(y_noise,x,M):
    
    design_matrix  = np.asmatrix(np.ones(len(x))).T
    for i in range(1,M+1):
        arr_sin = np.asmatrix(np.sin(i*x)).T
        design_matrix  = np.concatenate((design_matrix ,arr_sin),axis=1)
        arr_cos = np.asmatrix(np.cos(i*x)).T
        design_matrix  = np.concatenate((design_matrix ,arr_cos),axis=1)
    
    coef = (design_matrix.T*design_matrix).I*(design_matrix.T*(np.asmatrix(y_noise).T))
    return np.asarray(coef)

def approx_plot(coef,x,M):
    y = np.ones(len(x))*coef[0,0]
    for i in range(1,M+1):
        y = y + np.sin(i*x)*coef[2*i-1,0] + np.cos(i*x)*coef[2*i,0]

    plt.plot(x,y,'r')

if __name__ == '__main__':
    x = np.linspace(0,4,100)
    y, y_noise = gen_data(x)
    plt.plot(x,y,'b')
    plt.plot(x,y_noise,'g+')
    
    M = 8
    coef = least_squares_approx(y_noise,x,M)
    approx_plot(coef,x,M)
    plt.legend(labels=['original data','noise data','least square'],loc='upper left')
    plt.title('$y=2\sin(2\pi x)+3\cos(3\pi x)$')
    plt.show()

运行结果：