离散数学复习必备（命题）

第一章

命题：用一个陈述句表示的一个或多个为真为假，但不能同时为真又为假的判断句（或判断结果唯一的陈述句，或客观上存在唯一真值的陈述句）
命题的真值：只能是命题为“真”或“假”
例：（Y、F表示是否是命题）

• 1.北京是中国的首都        Y真
  -2.2+3=6                          Y假
• 请关上门。                      F
• 除地球外的星球有生物    Y 真值确定但未知
• 多漂亮的花啊                  F
• 我只给所有不给自己理发的人理发    悖论

命题变量：通常用p、q、r…表示命题变量。命题变量没有真值，只有一个确定的命题后，才有真值。

• 可以用p表示命题“2+3=5”则p是正确的。
  简单命题（原子命题）：不能分解为更简单的陈述句的命题
  简单命题：”北京是中国的首都“
  复合命题：有两个或几个简单句和连接词组成的命题。
  复合命题：”如果明天天气好，我们就去爬山“
  符号命题化：用英文字母或英文字母和连接词的组合表示命题，称为命题符号化。连接词———>连词

连接词

• 否定：（┐）
  设p是一个命题，┐p表示一个新命题”非p“,当且仅当p为真时，p为假。
  例如：p:今天时晴天 ┐p:今天不是晴天
• 合取（∧）
  设p,q表示两个命题，p∧q可表示复合命题，”p且q“。当且仅当p和q的真值时为真时，p∧q真值为真
  例如：p:今天是晴天；q:今天去公园 。
  p∧q:今天是晴天并且今天去公园。
• 析取（∨）
  设p,q表示两个命题，p∨q可表示复合命题，”p或q“。当且仅当q和p同时为假的时候p∨q为假。
  例如：p:今天去看电影；q:今天去公园；
  p∨q今天去看电影或去公园。
  注意：自然语言中的“或”有“可兼或”（同或）和“不可兼或”（异或）两种。析取连接词代表的是可兼或。 异或有时候会用“⊕”来表示。
• 蕴含 （→）
  设p,q表示两个命题，p→q可表示复合命题，”如果p则q“。当且仅当p为真，q为假时，p→q的真值为假。
  例如：p:今天天气晴朗;q:我们去海滩；
  p→q如果今天天气晴朗我们就去海滩。
  p:为蕴含前件；q:为蕴含后件
  p是q的充分条件，q是p的必要条件
• 等价（↔）
  设p,q表示两个命题，p↔q可表示复合命题，”p当且仅当q“。P↔Q为真当且仅当P、Q同时为真假。
  例如：p:两个三角形是全等的；q:两个三角形的三条对应边相等
  p↔q：”两个三角形是全等的当且仅当两个三角形的三条对应边相等“
  优先级
  （）>>┐>>∧>>∨>>→>>↔
  连接词的真值表
  

命题公式

• 命题常元：代表特定的简单命题
• 命题变元：代表任意命题，取值为真或假的变量
• 命题公式
  
  • 一个含有命题变元的命题公式的真值是不确定的
  • 只有当公式中所有的命题变元被指定代表特定的命题时，命题公式才成为真命题，其真值才会被唯一确定。
• 公式的赋值
  定义：若命题公式A含有的全部命题变元为p1,p2,p3,p4…pn,给p1,p2,p3,p4…pn指定一组真值，称为为A的一个解释或赋值。使A的真值为真的赋值称为成真赋值，使A的真值为假的赋值为成假赋值。
  真值表：命题公式在所有可能的赋值下的取值的列表含n个变形的公式有2的n次方个赋值。
  
• 命题公式的分类
  • 若A在它的各种情况下赋值的取值均为真，则称A为重言式或永真式
  • 若A在它的各种情况下赋值的取值均为假，则称A为矛盾式或永假式
  • 若至少存在一种赋值能使A的真值为真，则称A为可满足式

等值演算

• 等价关系式
  定义：设A和B是两个命题（或命题公式），若A↔B是永真式，命题A和B称为逻辑等价的，可记作A⇔B
• 基本等价式
  
  置换规则：若公式G中的一部分A(包含G中的几个连续的符号)是公式，称A为G的子公式；用与A的逻辑等价的公式B置换A不改变公式G的真值。
  

其他连接词

• 与非
  

• 或非
  

• 异或
  

• 连接词的真值
  

范式

范式存在定理：任何一个命题公式都存在着与之等价的戏曲范式与合取范式。

• 极小项
  含有n个命题变元的合取中，若每个命题变元与其否定不同时出现，而二者之一必须出现且仅出现一次这样的合取式称为极小项
• 极大项
  含有n个命题变元的析取中，若每个命题变元与其否定不同时出现，而二者之一必须出现且仅出现一次这样的合取式称为极小项

主析取范式

定义：由若干个不同的小项组成的析取式称为主析取范式，与A等价的主析取范式称为A的主析取范式。


就是析取范式的每一项都必须含有p,q,r；如果哪项没有需要加上缺少的那一项，后续步骤省略了

主合取范式

定义：由若干个不同的小项组成的合取式称为主析取范式，与A等价的主合取范式称为A的主析取范式。

析（合）取的用途

1. 判断两个公式是否等价
   

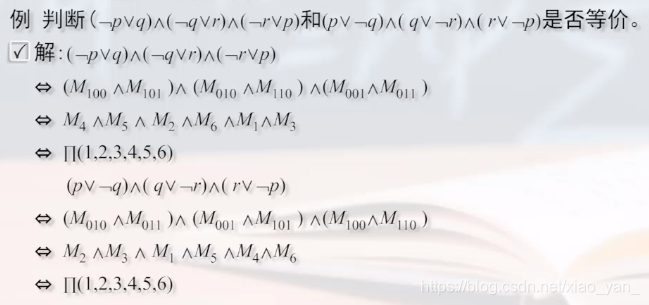
2. 求公式的成真赋值和成假赋值
   

3. 判断公式的类型

含有的极大项（极小项）为2的n次方个

推理逻辑

定义：当A和B是两个命题公式，当且仅当命题A→B是重言式时（即A→B⇔T时）称从A可推出B，或A蕴含B，或B是A的结论，可以表示成A⇒B
推理理论：一般的，推理的前提可以有多个，若（A1∧A2∧…∧An）→B是重言式，则称由前提A1，A2，…，An可推出结论B，可以表示为（A1∧A2∧…∧An）⇒B

推理证明方法

• 推理证明规则
  

• 例题
  
  

• 至此命题结束了是不是很有收获呢？