机器学习降维方法总结

最新推荐文章于 2023-01-06 10:56:47 发布

xiaoma_xiaoma

最新推荐文章于 2023-01-06 10:56:47 发布

阅读量1k

点赞数

原文链接：https://blog.csdn.net/ma416539432/article/details/53286028

版权

机器学习降维方法总结

前言

转载自：https://blog.csdn.net/ma416539432/article/details/53286028

前言

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。
目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们希望减少冗余信息所造成的误差,提高识别（或其他应用）的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。
在很多算法中，降维算法成为了数据预处理的一部分，如PCA。事实上，有一些算法如果没有降维预处理，其实是很难得到很好的效果的。

降维的作用：

降低时间复杂度和空间复
节省了提取不必要特征的开销
去掉数据集中夹杂的噪
较简单的模型在小数据集上有更强的鲁棒性
当数据能有较少的特征进行解释，我们可以更好的解释数据，使得我们可以提取知识。
实现数据可视化

说到维度，其目的是用来进行特征选择和特征提取，注意特征选择和特征提取这二者的不同之处：
特征选择：选择重要特征子集，删除其余特征。
特征提取：由原始特征形成较少的新特征。
在特征提取中，我们要找到k个新的维度的集合，这些维度是原来k个维度的组合，这个方法可以是监督的，也可以是非监督的，
pca-非监督的
lda（线性判别分析）-监督的
这两个都是线性投影来进行降为的方法。
另外，因子分析，和多维标定（mds）也是非监督的线性降为方法

降维方法从线性非线性的角度的划分

在这里插入图片描述

线性降维

子集选择
主成分分析（还有基于核方法的主成分分析）
因子分析
独立成分分析
线性判别分析
多维标定法（MDS）
矩阵分解：比如svd

1. 子集选择

属性子集选择1通过删除不相关或冗余的属性（或维）减少数据量。属性子集选择的目标是找出最小属性集，使得数据类的概率分布尽可能地接近使用所有属性得到的原分布。在缩小的属性集上挖掘还有其他的优点：它减少了出现在发现模式上的属性数目，使得模式更易于理解。

“如何找出原属性的一个‘好的’子集？”对于n个属性，有2n个可能的子集。穷举搜索找出属性的最佳子集可能是不现实的，特别是当n和数据类的数目增加时。因此，对于属性子集选择，通常使用压缩搜索空间的启发式算法。通常，这些方法是典型的贪心算法，在搜索属性空间时，总是做看上去是最佳的选择。它们的策略是做局部最优选择，期望由此导致全局最优解。在实践中，这种贪心方法是有效的，并可以逼近最优解。

“最好的”（和“最差的”）属性通常使用统计显著性检验来确定。这种检验假定属性是相互独立的。也可以使用一些其他属性评估度量，如建立分类决策树使用的信息增益度量2。

属性子集选择的基本启发式方法包括以下技术，其中一些在图3.6中给出。
在这里插入图片描述
这里要注意的是，我们选特征要在验证集上进行，而不是训练集上进行，一般来说，更多的特征对于训练集上的准确度是有帮助的，但是在测试集上就不一定了。

下面这里所说的最好属性，是说最能降低验证集合错误率的属性。

1)逐步向前选择：该过程由空属性集作为归约集开始，确定原属性集中最好的属性，并将它添加到归约集中。在其后的每一次迭代，将剩下的原属性集中的最好的属性添加到该集合中。
2)逐步向后删除：该过程由整个属性集开始。在每一步中，删除尚在属性集中最差的属性。
3)逐步向前选择和逐步向后删除的组合：可以将逐步向前选择和逐步向后删除方法结合在一起，每一步选择一个最好的属性，并在剩余属性中删除一个最差的属性。
4)决策树归纳：决策树算法（例如，ID3、C4.5和CART）最初是用于分类的。决策树归纳构造一个类似于流程图的结构，其中每个内部（非树叶）结点表示一个属性上的测试，每个分枝对应于测试的一个结果；每个外部（树叶）结点表示一个类预测。在每个结点上，算法选择“最好”的属性，将数据划分成类。

子集选择的缺点：
把属性和属性之间看成是完全独立的，有时候，一个X1和一个x2单独是不能提供什么信息的，但是x1和x2在一起就能够提供很多的信息，
例如：在人脸识别中，单一的维度是一个像素点，是不能提供有效的信息的，但是很多像素共同作用就能提供有效的组合特征。

子集选择实现：<待完善>

2. 主成分分析

在把讨论主成分分析的理论之前，我们看一下pca的直观理解。
在这里插入图片描述
这是我们数据的原始分布，如上图。现在我们想要用一组新的坐标来表示这个数据，往下看

我们新的坐标的选择方式：找到第一个坐标，数据集在该坐标的方差最大（方差最大也就是我们在这个数据维度上能更好的区分不同类型的数据），然后找到第二个坐标，该坐标与原来的坐标正交。该过程会一一直的重复，知道新坐标的数目与原来的特征个数相同，这时候我们会发现数据打大部分方差都在前面几个坐标上表示，这些新的维度就是我们所说的主成分。
再看面例子：
在这里插入图片描述
图片中有三类数据，我们发现在x这个维度上就能很好的区分三个类别，所以我们用pca降为得到下面的图片，如果不降维度。我们可以用比说决策树或者svm等方法的到分类的决策面，那么分类决策面是更复杂的。上面这个例子只是二维的情况，这种提升看起来作用不大，但是当数据是更高维度的时候，pca的意义就显现出来。

在进行pca分析之前，我们先对数据进行标准化处理。这个因为每个维度数据的分布是不同的，比说一个维度是0～2000，另一个维度是0～6 ；第二个维度的方差更小，但是这样是显然不对的。
在这里插入图片描述
这样处理之后，每个维度的数据分布都服从标准正态分布，均值0方差是1。（其中xi是第i维度的数据）

通过上面的论述，我们会发现，pca是一种线性降维的方法，对原始数据进行线性变换，然后新的数据其实原始数据的线性组合。而线性变换的方式是无穷多的，通过对线性变换进行一些限制。就产生了pca方法。
接下来讨论这些限制如何实现。

这里先解释一下投影的概念：
在这里插入图片描述

现在我们知道了，样本协方差矩阵对应的特征值就等于新样本数据在对应特征向量下的方差。
而我们的k值，也就是主成分的个数怎么选取呢？根据如下图：

我们最后想保留多少信息将决定我们最终选择几个k值。

Principal Component Analysis(PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。
通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA是丢失原始数据信息最少的一种线性降维方式。（实际上就是最接近原始数据，但是PCA并不试图去探索数据内在结构）
设n维向量w为目标子空间的一个坐标轴方向（称为映射向量），最大化数据映射后的方差，有：
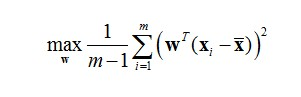
在这里插入图片描述
其中m是数据实例的个数， xi是数据实例i的向量表达， x拔是所有数据实例的平均向量。定义W为包含所有映射向量为列向量的矩阵，经过线性代数变换，可以得到如下优化目标函数：

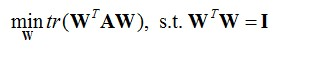
其中tr表示矩阵的迹：
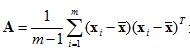
在这里插入图片描述
A是数据协方差矩阵。

容易得到最优的W是由数据协方差矩阵前k个最大的特征值对应的特征向量作为列向量构成的。这些特征向量形成一组正交基并且最好地保留了数据中的信息。
PCA的输出就是Y = W’X，由X的原始维度降低到了k维。

pca的不足之处：

（1）
（2）pca是线性降维方法，有时候数据之间的非线性关系是很重要的，这时候我们用pca会得到很差的结果。所有接下来我们引入核方法的pca。
（3）主成分分析法只在样本点服从高斯分布的时候比较有效。
（4）特征根的大小决定了我们感兴趣信息的多少。即小特征根往往代表了噪声，但实际上，向小一点的特征根方向投影也有可能包括我们感兴趣的数据；
（5）特征向量的方向是互相正交（orthogonal）的，这种正交性使得PCA容易受到Outlier的影响，例如在文献[1]中提到的例子；
（6）难于解释结果。例如在建立线性回归模型（Linear Regression Model）分析因变量（response）和第一个主成份的关系时，我们得到的回归系数（Coefficiency）不是某一个自变量（covariate）的贡献，而是对所有自变量的某个线性组合（Linear Combination）的贡献。
（7）原始的pca算法会把所有的数据一次性的放入内存中，这在大数据集的情况下有可能会遇到问题，所以有人提出了增量式的pca，这在sklearn中是有实现的。

3. 核方法的主成分分析

在讨论核方法的主成分分析之前，先要知道核方法，或者说核技巧（kernel trick）
是干什么的。关于这一点在李航的《统计学习方法》中讲的比较清楚。
在这里插入图片描述

我们看到通过对原来的样本点进行非线性的映射可以使的原来非线性可分的问题，在新的空间中线性可分。
上面的问题只是一个简化的例子，在实际的问题中我们的样本要复杂的多，我的样本维度要高的多了，我们对样本无法有像上面例子这样那么直观的认识，那么我们的的非线性映射 $\phi \left( {{x_i}} \right)$ 这个东西怎么确定呢？是随便确定一个它，然后对样本进行使用，然后在应用到我们实际的模型之上吗？可以想像这个过程是很难进行的。
然而通过核函数，或者说kenel trick，我们将大大的简化这个问题。
在这里插入图片描述

核技巧不仅仅能用用在支持向量机，只要原始的机器学习算法中有两个向量的内积，就可以尝试应用核技巧。

关于核的选择我们我们更多的时候是通过实验（在验证集上实验）来得到的。
下面总结一下常用核。看下面这个链接
http://scikit-learn.org/stable/modules/metrics.html#metrics

接下来看一下核技巧的pca算法。看下面这个链接。

https://zhuanlan.zhihu.com/p/21583787
（其实这个链接也并没看明白，数学太烂）
先有下面一个直观的认识吧。
在Kernel PCA分析之中，我们认为原有数据有更高的维数，我们可以在更高维的空间（Hilbert Space）中做PCA分析（即在更高维空间里，把原始数据向不同的方向投影）。这样做的优点有：对于在通常线性空间难于线性分类的数据点，我们有可能再更高维度上找到合适的高维线性分类平面。

pca的一个实际使用的例子

import numpy as np
import matplotlib.pyplot as plt

from sklearn import linear_model, decomposition, datasets
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV

logistic = linear_model.LogisticRegression()

pca = decomposition.PCA()
pipe = Pipeline(steps=[('pca', pca), ('logistic', logistic)])

digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target
pca.fit(X_digits)

plt.figure(1, figsize=(4, 3))
plt.clf()
plt.axes([.2, .2, .7, .7])
plt.plot(pca.explained_variance_, linewidth=2)
plt.axis('tight')
plt.xlabel('n_components')
plt.ylabel('explained_variance_')

在这里插入图片描述

n_components = [20, 40, 64]
Cs = np.logspace(-4, 4, 3)

#Parameters of pipelines can be set using ‘__’ separated parameter names:

estimator = GridSearchCV(pipe,
                         dict(pca__n_components=n_components,
                              logistic__C=Cs))
estimator.fit(X_digits, y_digits)

plt.axvline(estimator.best_estimator_.named_steps['pca'].n_components,
            linestyle=':', label='n_components chosen')
plt.legend(prop=dict(size=12))
plt.show()

最后我们得到结，在20，40，64。三个主成分的数量选择中，通过与逻辑回归的交叉选择，我们最后认为40个主要成分在后面的逻辑回归上有更好的选择。在这个例子上说明，虽然pca是一种无监督的降维方法，我们在最后选择合适的维度的时候，还是要通过在训练集上的验证得到。所以我们主成成分的个数n可以看成是一个超参数。

4. 线性判别分析（LDA）

我们会先叙述LDA的原理，然后看一个LDA的例子，然后在同一个例子上面我们讨论LDA和PCA降维方法的异同点。

http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024389.html
LDA算法的原理就看一下这位大神的分析把。
http://bluewhale.cc/2016-04-10/linear-discriminant-analysis.html
这里讲述了线性判别算法的具体计算过程。

自我感觉，线性判别方法和逻辑回归，svm一样都是在找一个好的分类的超平面，而LDA是一种直接的方法，通过样本的原始分布计算出来，而逻辑回归，svm，感知机等寻找超平面。都是一种迭代的方法，通过随机梯度下降来渐进的拟合出能够分类数据的超平面。

http://scikit-learn.org/stable/modules/generated/sklearn.discriminant_analysis.LinearDiscriminantAnalysis.html#sklearn.discriminant_analysis.LinearDiscriminantAnalysis
这个链接里面简述了LDA在sklearn中的实现。注意LDA应用权重缩减之后的效果会得到显著的提升，这也从侧面应证了lda和lR等算法的一致性。

在iris数据集上实验LDA算法和LR算法，看看两个算法的效果差异。

参考自：https://blog.csdn.net/rosenor1/article/details/52278116
Linear Discriminant Analysis(也有叫做Fisher Linear Discriminant)是一种有监督的（supervised）线性降维算法。与PCA保持数据信息不同，LDA是为了使得降维后的数据点尽可能地容易被区分！

假设原始数据表示为X，（m*n矩阵，m是维度，n是sample的数量）

既然是线性的，那么就是希望找到映射向量a，使得 a‘X后的数据点能够保持以下两种性质：

1、同类的数据点尽可能的接近（within class）

2、不同类的数据点尽可能的分开（between class）

所以呢还是上次PCA用的这张图，如果图中两堆点是两类的话，那么我们就希望他们能够投影到轴1去（PCA结果为轴2），这样在一维空间中也是很容易区分的。

在这里插入图片描述

目标函数就是最后一行J（a)，μ（一飘）就是映射后的中心用来评估类间距，s（一瓢）就是映射后的点与中心的距离之和用来评估类内距。J(a)正好就是从上述两个性质演化出来的。

因此两类情况下：
加上a’a=1的条件（类似于PCA）
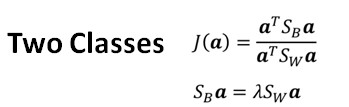
在这里插入图片描述
可以拓展成多类：

以上公式推导可以具体参考pattern classification书中的相应章节，讲fisher discirminant的

OK，计算映射向量a就是求最大特征向量，也可以是前几个最大特征向量组成矩阵A=[a1,a2,….ak]之后，就可以对新来的点进行降维了： y = A’X （线性的一个好处就是计算方便！）

可以发现，LDA最后也是转化成为一个求矩阵特征向量的问题，和PCA很像，事实上很多其他的算法也是归结于这一类，一般称之为谱（spectral）方法。

线性降维算法我想最重要的就是PCA和LDA了。

5. 奇异值分解（svd）

参考链接：

http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html
机器学习实战

关于特征值分解的理论看上面这个链接都可以了。
特征值分解用于推荐系统的两个例子：

（1）直接使用svd方法来进行推荐
这个方法只用到了svd算法。

把上表当作一个矩阵，
然后进行，非负矩阵分解，或者svd分解，
利用分解后的矩阵重构出一个新的矩阵
这时新重构的矩阵在原来没有评分的矩阵已经有了评分
然后在新的矩阵中将用户打过分的物品过滤掉
最后为用户推荐得分最高的物品。
具体参考这篇论文。
（2）svd算法和协同过滤的组合算法
在机器学习实战中有实现。
这个代码先实现了一个基于物品相似度的推荐
一个用户，我们想预测他没有评分的物品，一种最简单的方法是，把它对物品所有的评分算一个平均数。
基于物品相似度的改进：
在计算平均值时，我们认为和待评分物品相似的物品应有越大的权值，
所以我们计算待评分物品和该用户评估分物品的相似度
然后进行加权平均。
而这里svd的应用就是通过

	U, Sigma, VT = la.svd(dataMat)
    Sig4 = mat(eye(4) * Sigma[:4])  # arrange Sig4 into a diagonal matrix
    xformedItems = dataMat.T * U[:, :4] * Sig4.I

这一段代码，将矩阵按照的行进行降维，
将代表物品的向量从n（n个用户）的空间降到k个
（k个主题）中去，然后在新的特征空间进行相似度的计算。

'''
Created on Mar 8, 2011

@author: Peter
'''
from numpy import *
from numpy import linalg as la


def loadExData():
    return [[0, 0, 0, 2, 2],
            [0, 0, 0, 3, 3],
            [0, 0, 0, 1, 1],
            [1, 1, 1, 0, 0],
            [2, 2, 2, 0, 0],
            [5, 5, 5, 0, 0],
            [1, 1, 1, 0, 0]]


def loadExData2():
    return [[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
            [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
            [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
            [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
            [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
            [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
            [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
            [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
            [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
            [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
            [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]


def ecludSim(inA, inB):
    return 1.0 / (1.0 + la.norm(inA - inB))


def pearsSim(inA, inB):
    if len(inA) < 3: return 1.0
    return 0.5 + 0.5 * corrcoef(inA, inB, rowvar=0)[0][1]


def cosSim(inA, inB):
    num = float(inA.T * inB)
    denom = la.norm(inA) * la.norm(inB)
    return 0.5 + 0.5 * (num / denom)


def standEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0;
    ratSimTotal = 0.0
    for j in range(n):
        userRating = dataMat[user, j]
        if userRating == 0: continue
        overLap = nonzero(logical_and(dataMat[:, item].A > 0, \
                                      dataMat[:, j].A > 0))[0]
        if len(overLap) == 0:
            similarity = 0
        else:
            similarity = simMeas(dataMat[overLap, item], \
                                 dataMat[overLap, j])
        print 'the %d and %d similarity is: %f' % (item, j, similarity)
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0:
        return 0
    else:
        return ratSimTotal / simTotal


def svdEst(dataMat, user, simMeas, item):
    n = shape(dataMat)[1]
    simTotal = 0.0;
    ratSimTotal = 0.0
    U, Sigma, VT = la.svd(dataMat)
    Sig4 = mat(eye(4) * Sigma[:4])  # arrange Sig4 into a diagonal matrix
    xformedItems = dataMat.T * U[:, :4] * Sig4.I  # create transformed items
    for j in range(n):
        userRating = dataMat[user, j]
        if userRating == 0 or j == item: continue
        similarity = simMeas(xformedItems[item, :].T, \
                             xformedItems[j, :].T)
        print 'the %d and %d similarity is: %f' % (item, j, similarity)
        simTotal += similarity
        ratSimTotal += similarity * userRating
    if simTotal == 0:
        return 0
    else:
        return ratSimTotal / simTotal


def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
    unratedItems = nonzero(dataMat[user, :].A == 0)[1]  # find unrated items
    if len(unratedItems) == 0: return 'you rated everything'
    itemScores = []
    for item in unratedItems:
        estimatedScore = estMethod(dataMat, user, simMeas, item)
        itemScores.append((item, estimatedScore))
    return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]

6. 因子分析

1）因子分析原理
2）因子分析和主成分分析的比较
3）因子分析的sklean实现
4）因子分析和主成分分析的实验对比

在这里插入图片描述
因子分析的基本思想：
根据相关性的大小把原始变量分组，使得同组内的变量相关性高，不同组的变量相关性低。

因子分析的求解过程

关于因子分析的流程可以参考一下这个链接。

在这里插入图片描述

非线性降维方法

1. 局部线性嵌入（LLE）

Locally linear embedding（LLE）[1] 是一种非线性降维算法，它能够使降维后的数据较好地保持原有 流形结构 。LLE可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与LLE有密切联系。

见图1，使用LLE将三维数据（b）映射到二维（c）之后，映射后的数据仍能保持原有的数据流形（红色的点互相接近，蓝色的也互相接近），说明LLE有效地保持了数据原有的流行结构。

但是LLE在有些情况下也并不适用，如果数据分布在整个封闭的球面上，LLE则不能将它映射到二维空间，且不能保持原有的数据流形。那么我们在处理数据中，首先假设数据不是分布在闭合的球面或者椭球面上。

在这里插入图片描述
图1 LLE降维算法使用实例

LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。算法的主要步骤分为三步：(1)寻找每个样本点的k个近邻点；（2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；（3）由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。具体的算法流程如图2所示：
在这里插入图片描述
图 2 LLE算法步骤

在这里插入图片描述

2. Laplacian Eigenmaps 拉普拉斯特征映射

继续写一点经典的降维算法，前面介绍了PCA,LDA，LLE，这里讲一讲Laplacian Eigenmaps。其实不是说每一个算法都比前面的好，而是每一个算法都是从不同角度去看问题，因此解决问题的思路是不一样的。这些降维算法的思想都很简单，却在有些方面很有效。这些方法事实上是后面一些新的算法的思路来源。

Laplacian Eigenmaps[1] 看问题的角度和LLE有些相似，也是用局部的角度去构建数据之间的关系。

它的直观思想是希望相互间有关系的点（在图中相连的点）在降维后的空间中尽可能的靠近。Laplacian Eigenmaps可以反映出数据内在的流形结构。

在这里插入图片描述
使用时算法具体步骤为：

步骤1：构建图

使用某一种方法来将所有的点构建成一个图，例如使用KNN算法，将每个点最近的K个点连上边。K是一个预先设定的值。

步骤2：确定权重

确定点与点之间的权重大小，例如选用热核函数来确定，如果点i和点j相连，那么它们关系的权重设定为：

在这里插入图片描述
使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。

前面提到过，Laplacian Eigenmap具有区分数据点的特性，可以从下面的例子看出：

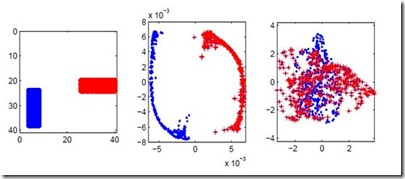
在这里插入图片描述
图1 Laplacian Eigenmap实验结果

见图1所示，左边的图表示有两类数据点（数据是图片），中间图表示采用Laplacian Eigenmap降维后每个数据点在二维空间中的位置，右边的图表示采用PCA并取前两个主要方向投影后的结果，可以清楚地看到，在此分类问题上，Laplacian Eigenmap的结果明显优于PCA。

在这里插入图片描述
图2 roll数据的降维

图2说明的是，高维数据（图中3D）也有可能是具有低维的内在属性的（图中roll实际上是2D的），但是这个低维不是原来坐标表示，例如如果要保持局部关系，蓝色和下面黄色是完全不相关的，但是如果只用任何2D或者3D的距离来描述都是不准确的。

下面三个图是Laplacian Eigenmap在不同参数下的展开结果（降维到2D），可以看到，似乎是要把整个带子拉平了。于是蓝色和黄色差的比较远。

文章出处：http://blog.csdn.net/xbinworld?viewmode=contents

从监督与非监督的角度分

PCA无监督，LDA有监督。

xiaoma_xiaoma

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
机器学习降维方法总结

机器学习降维方法总结前言降维方法从线性非线性的角度的划分线性降维1. 子集选择2. 主成分分析3. 核方法的主成分分析pca的一个实际使用的例子4. 线性判别分析（LDA）5. 奇异值分解（svd）6. 因子分析非线性降维方法1. [局部线性嵌入（LLE）](https://blog.csdn.net/xbinworld/article/details/8855771)2. [Laplacian...
复制链接

扫一扫