三维空间中圆的参数方程及matlab程序画图

原文链接： 三维空间中圆的参数方程

三维空间中，以点为圆心、以向量为法向量、半径为 r 的圆（见下图），

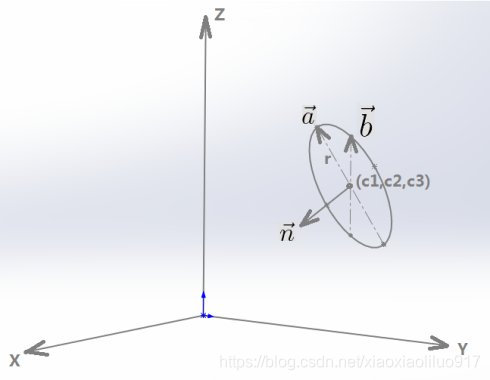
它的参数方程为：






其中，与分别对应单位向量与，它们既垂直于，又互相垂直；随着从0变化到
，通过参数方程可以得到圆上每一个点的坐标。

与是满足既垂直于，又互相垂直的任意单位向量。怎么样快速得到满足条件的与呢？这时候应该充分利用叉乘运算的特点，因为两个向量的叉乘结果只要不为零，叉乘结果总是垂直于原来的这两个向量。具体如下：

求的方法：叉乘坐标向量。如果叉乘结果不为零，那么它必然垂直于，把它单位化后就得到；如果叉乘结果恰好为零，再用叉乘剩下两个坐标向量与中任意一个，单位化叉乘结果，得到。

求的方法：叉乘上一步得到的，叉乘结果必然垂直于与，单位化叉乘结果，就得到。

接下来，利用Matlab软件对三维空间中圆的参数方程进行测试。代码如下：

n=[1 1 1]; %法向量n
r=1; %圆的半径为1
c=[1 1 1]; %圆心的坐标
theta=(0:2*pi/100:2*pi)'; %theta角从0到2*pi
a=cross(n,[1 0 0]); %n与i叉乘，求取a向量
if ~any(a) %如果a为零向量，将n与j叉乘
    a=cross(n,[0 1 0]);
end
b=cross(n,a); %求取b向量
a=a/norm(a); %单位化a向量
b=b/norm(b); %单位化b向量

c1=c(1)*ones(size(theta,1),1);
c2=c(2)*ones(size(theta,1),1);
c3=c(3)*ones(size(theta,1),1);

x=c1+r*a(1)*cos(theta)+r*b(1)*sin(theta);%圆上各点的x坐标
y=c2+r*a(2)*cos(theta)+r*b(2)*sin(theta);%圆上各点的y坐标
z=c3+r*a(3)*cos(theta)+r*b(3)*sin(theta);%圆上各点的z坐标

plot3(x,y,z)
xlabel('x轴')
ylabel('y轴')
zlabel('z轴')

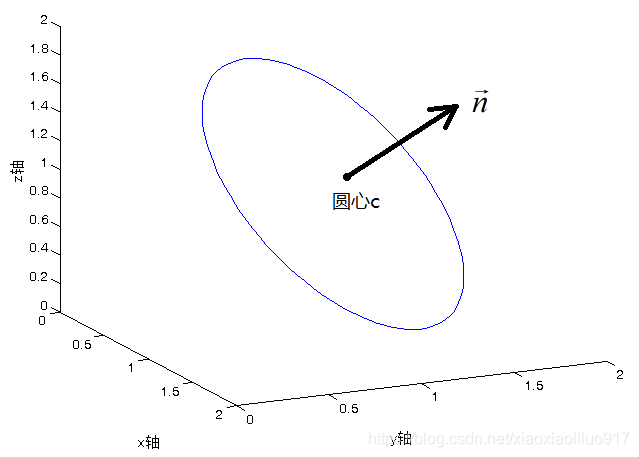
Matlab运行结果如下图：