从生物进化到代码世界：遗传算法全解析-CSDN博客

在计算机科学与人工智能的浩瀚星空中，遗传算法（Genetic Algorithm, GA）宛如一颗璀璨的明星，以其独特的仿生学理念和强大的优化能力，为众多复杂问题的求解开辟了新的路径。它诞生于 20 世纪 70 年代，由美国密歇根大学的 John Holland 教授提出，灵感源于达尔文的生物进化论和孟德尔的遗传学理论，将自然选择、遗传变异等生物进化现象转化为一种高效的计算模型，用于寻找复杂问题的最优解或近似最优解。

想象一下，在一个充满挑战的问题空间中，每个可能的解决方案都是一个独特的个体，它们如同自然界中的生物一样，拥有各自的 “基因”。遗传算法就像是一场模拟的进化旅程，通过不断地选择、交叉和变异，让适应环境（即更接近最优解）的个体有更多机会繁衍后代，而不适应的个体则逐渐被淘汰。在这个过程中，种群不断进化，朝着最优解的方向不断逼近。

这种独特的优化机制，使得遗传算法在诸多领域展现出了巨大的潜力。无论是在工程设计中寻找最优的参数组合，还是在机器学习中优化模型的性能；无论是在生产调度里合理安排资源，还是在数据分析中挖掘隐藏的模式，遗传算法都能大显身手，为解决实际问题提供了强有力的支持。

模拟进化：遗传算法的基本原理

（一）生物进化启发下的算法思想

遗传算法的核心思想深深扎根于生物进化理论。在自然界中，生物通过遗传将自身的特征传递给后代，同时在环境的选择压力下，那些更适应环境的个体有更大的生存和繁衍机会，这就是 “适者生存” 的自然选择法则。遗传算法将这一过程抽象到计算领域，把问题的每个可能解看作一个生物个体，解的质量对应个体的适应度。通过模拟遗传和自然选择，算法在解空间中不断搜索，逐步逼近最优解。

（二）核心遗传操作详解

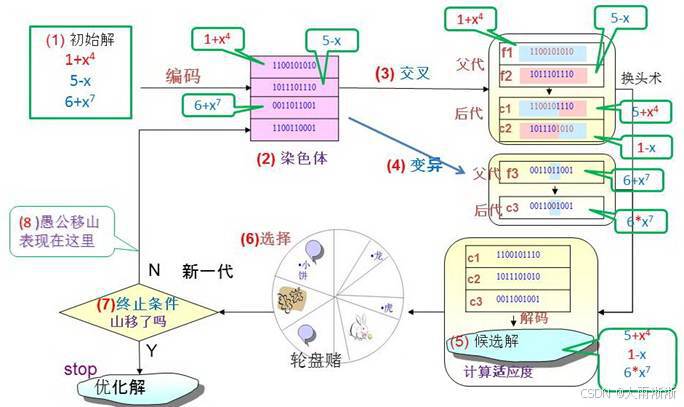
选择：选择操作是遗传算法中体现 “适者生存” 的关键步骤。它依据个体的适应度，从当前种群中挑选出更有可能产生优质后代的个体。常见的选择方法有轮盘赌选择和锦标赛选择。轮盘赌选择就像转动一个按照个体适应度比例划分区域的轮盘，适应度越高的个体，在轮盘上所占的区域越大，被选中的概率也就越高。例如，在一个包含 5 个个体的种群中，个体 A、B、C、D、E 的适应度分别为 10、20、30、40、50，那么它们被选中的概率分别为 10/150、20/150、30/150、40/150、50/150。锦标赛选择则是随机选取若干个个体进行 “比赛”（比较适应度），每次选择其中适应度最高的个体进入下一代，这种方式能有效避免轮盘赌选择中可能出现的随机性过大问题。

交叉：交叉操作模拟了生物繁殖过程中的基因重组。它从选择出的个体中随机挑选两个作为父代，按照一定的策略交换它们的部分基因，从而生成新的子代个体。单点交叉是最基本的交叉策略，它在父代个体的基因序列上随机选择一个点，将两个父代个体在该点之后的基因片段进行交换。假设有两个父代个体 P1=[1 0 1 1 0] 和 P2=[0 1 0 0 1]，若随机选择的交叉点为第 3 位，那么交叉后生成的子代个体 C1=[1 0 0 0 1] 和 C2=[0 1 1 1 0]。两点交叉则是随机选择两个交叉点，交换这两个交叉点之间的基因片段；均匀交叉更为灵活，它对每个基因位都以一定概率决定是否进行交换，使得子代个体的基因来源更加多样化。

变异：变异操作以较小的概率对个体的基因进行随机改变，为种群引入新的基因信息，防止算法过早陷入局部最优解。在二进制编码中，变异可能表现为将基因位上的 0 变为 1，或 1 变为 0。例如，个体 [1 0 1 1 0] 在第 2 位发生变异后，就变成了 [1 1 1 1 0] 。变异操作虽然改变的幅度较小，但却能在算法搜索过程中起到关键的探索作用，帮助算法跳出局部最优的陷阱，维持种群的多样性。