Android OpenGLES2.0开发（四）：矩阵变换和相机投影

如果可以003

已于 2024-10-08 14:05:01 修改

阅读量788

点赞数 27

分类专栏： Android OpenGL ES 文章标签： android 矩阵数码相机 OpenGL ES

于 2024-10-08 09:00:00 首次发布

本文链接：https://blog.csdn.net/xiaozhiwz/article/details/142488394

版权

Android OpenGL ES 专栏收录该内容

8 篇文章 0 订阅

订阅专栏

事物的本质是事物本身所固有的、深藏于‌现象背后并决定或支配现象的方面‌。

请添加图片描述
还记得我们上一篇绘制的三角形吗，我们确实能够顺利用OpenGL ES绘制出图形了，这是一个好的开始，但这还远远不够。我们定义的坐标是正三角形，但是绘制出来三角形却拉升了（横屏显示会压缩）。

请添加图片描述
为了方便大家，我们将OpenGL ES坐标系图再次贴出。OpenGL ES的坐标系是一个正方形，他的四个顶点分别对应GLSurfaceView的四个顶点，这个是定死的我们无法改变，那要怎么才能让我的三角形变成等边三角形呢？既然坐标系为正方形，那么我们让GLSurfaceView也为正方形是否可行呢？

1. 方式一：设置GLSurfaceView宽高相等

注意这里有个误区就是OpenGL ES坐标顶点对应的是GLSurfaceView的四个顶点，而不是屏幕的四个顶点。所以好多文章说变形拉升什么的，甚至是官方文档都和手机屏幕扯上关系。我现在可以明确的告诉大家的是，这和手机的屏幕一点关系也没有。

那为什么又要说和屏幕有关系，其本质是将GLSurfaceView的宽高使用了match_parent导致GLSurfaceView大小和屏幕相同而已，但是变形拉升只和GLSurfaceView的大小有关，GLSurfaceView如果不是一个正方形，那么画出的图形就会变形。

既然我们知道了上述缘由后，最简单的方式就有了，就是设置GLSurfaceView的宽高相等即可:

<com.android.xz.opengldemo.view.TriangleGLSurfaceView
    android:layout_width="400dp"
    android:layout_height="400dp"/>

运行看看效果是否可行：
请添加图片描述
不出我们所料，果然是行得通的！！！

但是世界的运行往往不是我们人为能控制的，GLSurfaceView的宽高往往不是正方形，他要和应用相结合，他可能是游戏全屏界面，也可能是某个显示视频的预览界面，亦或是嵌到某个犄角旮旯充当不重要的视图，这个时候我们就引入了下面的方式。

2. 方式二：修改顶点坐标数据

当GLSurfaceView的宽高不一致的时，我们该如何是好？？？就比如我们现在GLSurfaceView是全屏的。

我们来分析下，GLSurfaceView目前全屏后，视图高被拉升了，原本三角形的top顶点到底边的垂直距离是0.866，也就是说我们按照GLSurfaceView拉升比缩放这个距离是不是也是可行的？

    // 三角形三个点的坐标，逆时针绘制
    static float triangleCoords[] = {   // 坐标逆时针顺序
            0.0f, 0.616f, 0.0f, // top
            -0.5f, -0.25f, 0.0f, // bottom left
            0.5f, -0.25f, 0.0f  // bottom right
    };

好了开始动手干，我们在Triangle类中surfaceChanged方法中重新计算缩放后Y的坐标点，如下：

public void surfaceChanged(int width, int height) {
    // 设置OpenGL ES画布大小
    GLES20.glViewport(0, 0, width, height);

    float radio = (float) width / height;
    triangleCoords = new float[]{   // 坐标逆时针顺序
            0.0f, 0.616f * radio, 0.0f, // top
            -0.5f, -0.25f * radio, 0.0f, // bottom left
            0.5f, -0.25f * radio, 0.0f  // bottom right
    };
    // 初始化形状坐标的顶点字节缓冲区
    ByteBuffer bb = ByteBuffer.allocateDirect(
            // (number of coordinate values * 4 bytes per float)
            triangleCoords.length * 4);
    // use the device hardware's native byte order
    bb.order(ByteOrder.nativeOrder());

    // create a floating point buffer from the ByteBuffer
    vertexBuffer = bb.asFloatBuffer();
    // add the coordinates to the FloatBuffer
    vertexBuffer.put(triangleCoords);
    // set the buffer to read the first coordinate
    vertexBuffer.position(0);
}

查看效果：
请添加图片描述
其实在没有看到效果时，我已经猜到最后肯定会绘制出正三角形，当然看了效果我们也就踏实了。

OpenGL ES绘图变形，其本质无非就是要解决View的宽高比和OpenGL ES正方形坐标系的一个变换；如果View是正方形无需变换，长方形该缩放缩放。

目前我们是绘制了一个三角形，顶点只有三个，修改顶点坐标倒还不是那么复杂。如果我们要绘制更加复杂的图像，顶点有几十个上百个，我们又该如何一个一个修改顶点的缩放比呢？聪明的你可能又想到了，我用for循环遍历修改啊那样就会方便很多，那我只能说你这是小聪明，OpenGL ES为我们提供了一个大聪明的方式：矩阵变换

3. 方式三：矩阵变换

我们知道OpenGL ES的世界里是三维空间，我们要对三维空间中的点进行缩放、平移、旋转实际在数学中有一个好的方式就是用矩阵来计算。而矩阵的知识是大学线性代数中的，这个基础需要读者自己去补。

空间中点缩放变换，建议看下这篇文章：【深度好文】3D坐标系下的点的转换矩阵（平移、缩放、旋转、错切）

3.1 自定义矩阵缩放方法

接下来我们使用矩阵相乘变换点的坐标，定义缩放方法如下：

public static void scale(float[] coords, int stride, float sx, float sy, float sz) {
    float[] scaleM = {
            sx, 0, 0,
            0, sy, 0,
            0, 0, sz
    };

    for (int i = 0; i < coords.length; i += stride) {
        float x = coords[i];
        float y = coords[i + 1];
        float z = coords[i + 2];

        coords[i] = scaleM[0] * x;
        coords[i + 1] = scaleM[4] * y;
        coords[i + 2] = scaleM[8] * z;
    }
}

修改surfaceChanged缩放坐标代码

public void surfaceChanged(int width, int height) {
    // 设置OpenGL ES画布大小
    GLES20.glViewport(0, 0, width, height);

    scale(triangleCoords, 3, 1, (float) width / height, 1);
    // 初始化形状坐标的顶点字节缓冲区
    ByteBuffer bb = ByteBuffer.allocateDirect(
            // (number of coordinate values * 4 bytes per float)
            triangleCoords.length * 4);
    // use the device hardware's native byte order
    bb.order(ByteOrder.nativeOrder());

    // create a floating point buffer from the ByteBuffer
    vertexBuffer = bb.asFloatBuffer();
    // add the coordinates to the FloatBuffer
    vertexBuffer.put(triangleCoords);
    // set the buffer to read the first coordinate
    vertexBuffer.position(0);
}

运行查看效果，也可得到正三角形。

3.2 使用GLSL缩放

上面方式固然可行，但是大量顶点计算都在CPU端了，如何使用GPU程序去并行计算？

OpenGL ES也提供了矩阵相乘的方式，在三维图形学中，一般使用的是4阶矩阵。在DirectX中使用的是行向量，如[xyzw]，所以与矩阵相乘时，向量在前矩阵在后。OpenGL中使用的是列向量，如[xyzx]T，所以与矩阵相乘时，矩阵在前，向量在后，我们最终通过“变换矩阵”来得到我们想要的向量。

修改顶点着色器代码并定义变换矩阵如下：

// 顶点着色器代码
private final String vertexShaderCode =
        // 传入变换矩阵
        "uniform mat4 uMVPMatrix;" +
                "attribute vec4 vPosition;" +
                "void main() {" +
                // 变换矩阵与顶点坐标相乘等到新的坐标
                "  gl_Position = uMVPMatrix * vPosition;" +
                "}";

/**
 * Shader程序中矩阵属性的句柄
 */
private int vPMatrixHandle;

// 最终变化矩阵
private final float[] mMVPMatrix = new float[16];

记得在surfaceCreated中获取矩阵属性句柄

public void surfaceCreated() {
	...
    // 获取绘制矩阵句柄
    vPMatrixHandle = GLES20.glGetUniformLocation(mProgram, "uMVPMatrix");
}

在surfaceChanged中设置缩放矩阵

    public void surfaceChanged(int width, int height) {
        // 设置OpenGL ES画布大小
        GLES20.glViewport(0, 0, width, height);

        float radio = (float) width / height;
        float[] scaleMatrix = new float[]{
                1, 0, 0, 0,
                0, radio, 0, 0,
                0, 0, 1, 0,
                0, 0, 0, 1
        };
        // 将缩放矩阵拷贝到变换矩阵中
        System.arraycopy(scaleMatrix, 0, mMVPMatrix, 0, scaleMatrix.length);
    }

在draw方法中将缩放矩阵传给OpenGL ES程序

public void draw() {
    ...
    
    // 将缩放矩阵传递给着色器程序
    GLES20.glUniformMatrix4fv(vPMatrixHandle, 1, false, mMVPMatrix, 0);

    // 画三角形
    GLES20.glDrawArrays(GLES20.GL_TRIANGLES, 0, vertexCount);

    // 禁用顶点阵列
    GLES20.glDisableVertexAttribArray(positionHandle);
}

运行查看效果，也可得到正三角形。

本文到现在已经讲了很多种方式可以正确绘制正三角形，但是到现在还没有到正真要讲的内容。我们发现将缩放矩阵传入着色器程序貌似已经完成了最终的目的，如果我们仅仅只是为了把三角形画正那么到这里应该就结束了。世界的运行往往出乎我们的意料，现在可能要求你缩放，但是未来可能还会平移、二维旋转、三维旋转、镜像等等操作，如果要我们去定义各种矩阵，那简直是灾难，于是下面的方式就应运而生了。

4. 相机和投影

投影：OpenGL 中主要有两种投影模式，分别是正交投影和透视投影
相机：相机视图顾名思义就相当于站在相机的角度观察某个物体，相机会看到投影到近平面的物体

4.1 投影

OpenGL提供了两种投影变换矩阵如下
请添加图片描述

透视投影
请添加图片描述

学过素描的应该都知道透视图的概念，符合人眼习惯，呈现近大远小的效果。

/**
 * @param m 生成的投影矩阵,float[4*4]
 * @param mOffset 填充时候起始的偏移量
 * @param left  近平面left边的x坐标
 * @param right 近平面right边的x坐标
 * @param bottom  近平面bottom边的y坐标
 * @param top   近平面top边的y坐标
 * @param near  近平面距离摄像机的距离
 * @param far   远平面距离摄像机的距离
 */
public static void frustumM(float[] m, int mOffset,
        float left, float right, float bottom, float top,
        float near, float far) {
}

正交投影
请添加图片描述

该投影方式图像大小不会随着距离变化而变化

/**
 * @param m 生成的投影矩阵,float[4*4]
 * @param mOffset 填充时候起始的偏移量
 * @param left  近平面left边的x坐标
 * @param right 近平面right边的x坐标
 * @param bottom  近平面bottom边的y坐标
 * @param top   近平面top边的y坐标
 * @param near  近平面距离摄像机的距离
 * @param far   远平面距离摄像机的距离
 */
public static void orthoM(float[] m, int mOffset,
        float left, float right, float bottom, float top,
        float near, float far) {
}

不管是正交投影还是透视投影，最终都是将视景体内的物体投影在近平面上，这也是 3D 坐标转换到 2D 坐标的关键一步。
而近平面上的坐标接着也会转换成归一化设备坐标，再映射到屏幕视口上。
为了解决之前的图像拉伸问题，就是要保证近平面的宽高比和视口的宽高比一致，而且是以较短的那一边作为 1 的标准，让图像保持居中。

4.2 相机

相机位置设置

/**
 *
 * @param rm 生成的摄像机矩阵，float[16]
 * @param rmOffset 填充时候的起始偏移量
 * @param eyeX 摄像机x坐标
 * @param eyeY 摄像机y坐标
 * @param eyeZ 摄像机z坐标
 * @param centerX 观察目标点的x坐标
 * @param centerY 观察目标点的y坐标
 * @param centerZ 观察目标点的z坐标
 * @param upX 摄像机up向量在x上的分量
 * @param upY 摄像机up向量在y上的分量
 * @param upZ 摄像机up向量在z上的分量
 */
public static void setLookAtM(float[] rm, int rmOffset,
        float eyeX, float eyeY, float eyeZ,
        float centerX, float centerY, float centerZ, float upX, float upY,
        float upZ) {
}

eyeX，eyeY，eyeZ：摄像机坐标。
centerX，centerY，centerZ:观察点坐标，和摄像机坐标一起决定了摄像机的观察方向，即向量(centerX - eyeX, centerY - eyeY, centerZ - eyeZ)。观察方向不朝向视景体是无法看到的。
upX，upY，upZ:摄像机up向量。相对于人眼观察物体中，人头的朝向，头的朝向影响了最后的成像。同样以图来说明：

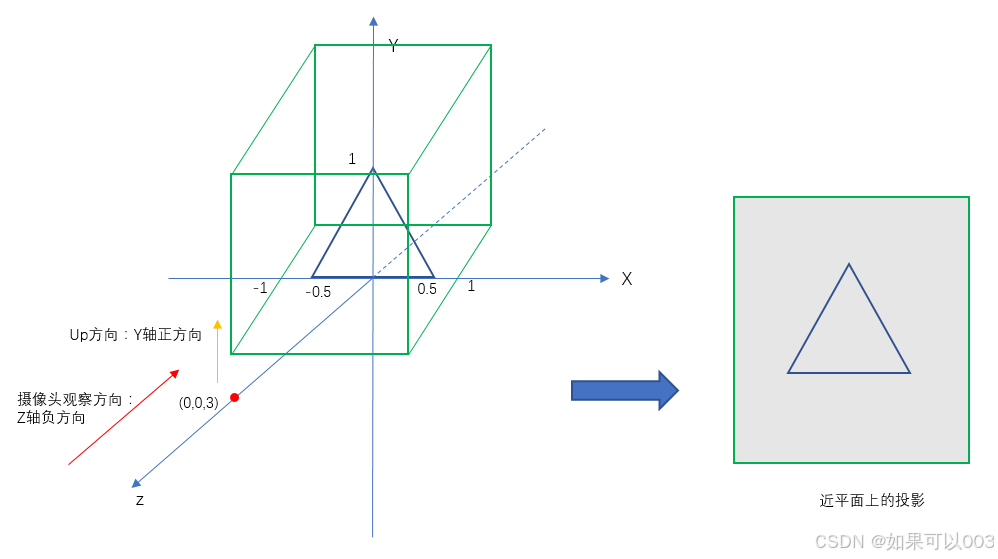
请添加图片描述
当up向量为Y的正方向时，正如我们头顶对着天花板，所以观察到的物体是正的，投影在近平面的样子就是正的，如右图

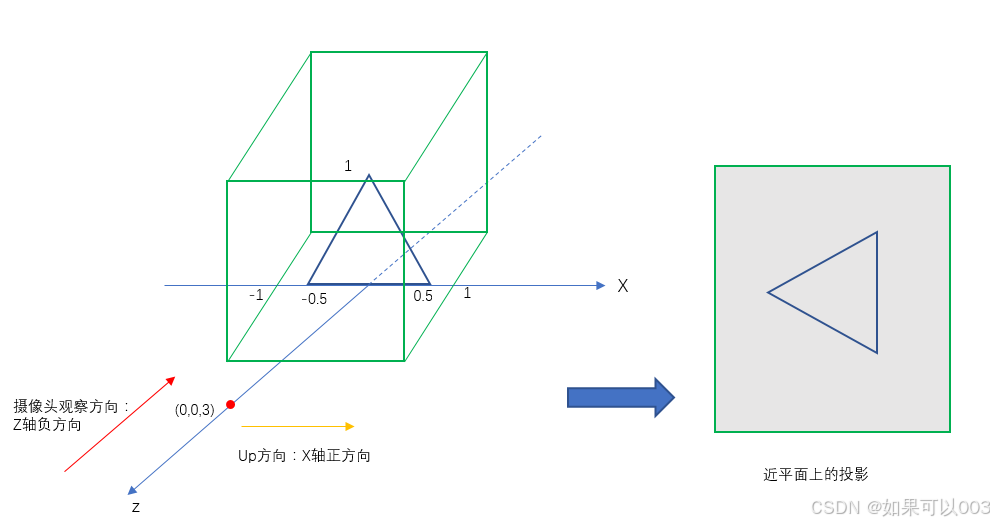
请添加图片描述
当up向量为X正方向时，正如我们向右90度歪着脑袋去看这个三角形，看到的三角形就会是向左旋转了90度的三角形

再比如up向量如果为Z轴正方向，就相当于仰着头去看这个三角形，但是因为我们的up向量和观察方向平行了，所以我们什么也看不到，就比如仰着头去看你身前的物体时，你什么也看不到。

所以在设置up向量时，一般总是设置为(0,1,0)，这是大多数观察时头朝上的方向。注意：up向量的大小无关紧要，有意义的只有方向。

4.3 near、far的取值范围规定

正交投影时，摄像机可位于视景体中间，此时near < 0，far > 0，近平面位于视点后面（Z轴正方向），远平面位于视点前面（Z轴负方向）
正交投影时，视景体也可位于视点后面(Z轴正方向)，此时near < 0, far < 0
正交投影时，far 和 near没有规定的大小关系，既可以far > near 也可以 far < near，只要物体在视景体内都可以被观察到。
透视投影时，far>near>0；我们不考虑其他情况，我们默认就在Z轴上看物体
当centerZ - eyeZ>0时：近平面nearZ坐标=eyeZ+near，远平面farZ坐标=eyeZ+far;
当centerZ - eyeZ<0时：近平面nearZ坐标=eyeZ-near，远平面farZ坐标=eyeZ-far;
我们要保证物体Z坐标在nearZ和farZ之间就能看到，也就是物体在视景里就能看到。

4.4 构造模型矩阵

根据上面的理论知识，我们不用再手动构造一个缩放矩阵了，我们定义如下三个矩阵并进行变换

public class Triangle {
	...
    // vPMatrix是“模型视图投影矩阵”的缩写
    // 最终变化矩阵
    private final float[] mMVPMatrix = new float[16];
    // 投影矩阵
    private final float[] mProjectionMatrix = new float[16];
    // 相机矩阵
    private final float[] mViewMatrix = new float[16];

    public void surfaceChanged(int width, int height) {
        // 设置OpenGL ES画布大小
        GLES20.glViewport(0, 0, width, height);

        float ratio;
        if (width > height) {
            ratio = (float) width / height;
            // 横屏使用
            // 透视投影，特点：物体离视点越远，呈现出来的越小。离视点越近，呈现出来的越大
            // 该投影矩阵应用于对象坐标
            Matrix.frustumM(mProjectionMatrix, 0, -ratio, ratio, -1, 1, 3, 7);
        } else {
            ratio = (float) height / width;
            // 竖屏使用
            // 透视投影，特点：物体离视点越远，呈现出来的越小。离视点越近，呈现出来的越大
            // 该投影矩阵应用于对象坐标
            Matrix.frustumM(mProjectionMatrix, 0, -1, 1, -ratio, ratio, 3, 7);
        }

        Matrix.setLookAtM(mViewMatrix, 0,
                0, 0, 3f,
                0f, 0f, 0f,
                0f, 1.0f, 0.0f);

        // Calculate the projection and view transformation
        Matrix.multiplyMM(mMVPMatrix, 0, mProjectionMatrix, 0, mViewMatrix, 0);
    }
}