距离度量分类体系

本篇文章并不打算描述所有这些类别，要具体阐述它们的细节和意义实在有点困难。这个大纲的目的，第一：提供一个貌似详细的距离度量的分类体系，列出相关的关键字。 第二：就像一个词典一样供参考和查阅，如果需要了解具体的细节，可以参考wiki或者具体文献。     

大纲： 
1. 相似性和不相似性的定义 
2. 预备概念 
3. 距离度量 
    3.1  Numerical Data 
          3.1.1 欧拉距离(Euclidean Distance) 
          3.1.2 曼哈顿距离(Manhattan Distance) 
          3.1.3.最大距离(Maximum Distance) 
          3.1.4 明考夫斯基距离(MinKowski Distance) 
          3.1.5 马式距离（Mahalanobis Distance） 
          3.1.6 平均距离（Average Distance) 
          3.1.7 其他距离：Chord Distance，Geodesic distance,….. 
    3.2 Categorical Data 
         3.2.1. 简单匹配距离（Simple matching Distance) 
         3.2.2  其他匹配距离 
    3.3. Binary Data 
         3.3.1 Jaccard, Dice, Pearson, Yule, Russel-Rao, Sokal-Michener, Rogers-Tanimoto, Rogers-Tanimoto-a, Kulzinsky. 
    3.4  Mixed-type Data 
    3.5  Time Series Data 
    3.7  Other 
          3.7.1 Based on Longest Common Subsequence 
          3.7.2 Based on Probability Models 
          3.7.3 Based on Landmark Model 
          3.7.4 Based on Link Model 
    3.8 概率变量的相似性 
        3.8.1 Pearson 协方差 
        3.8.2 卡方统计（Chi-square Statistic) 
        3.8.3 基于最优预测( Optimal Class Prediction) 
        3.8.4 基于组的距离度量（Group-based Distance） 
          

定义： 
一直误解相似（similarity）度量和不相似（dissimilarity）度量，相似性度量在以前的一篇中已经描述过了，通常情况下不相似度量满足下面的三条性质：

1） 0<= s(x,y) <=1 
2)   s(x,x) = 1 
3)   s(x,y) = s(y,x)

当然，还有更多的相似度量和不相似度量方法（@see  representation of similarity matrices by trees）

预备概念： 
1. Proximity Matrix 
    给定数据集合D={x1,x2,x3,…,xn} 
    Mdis(D) = (dij)   dij = d(xi, xj)  
    Msim(D) = (sij)   sij = s(xi, xj)

2. 离差矩阵Scatter Matrix 
   

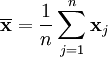
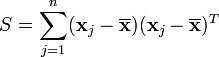或者 Cn是中心矩阵 Centering Matrix :

3. 协方差矩阵Covariance Matrix: