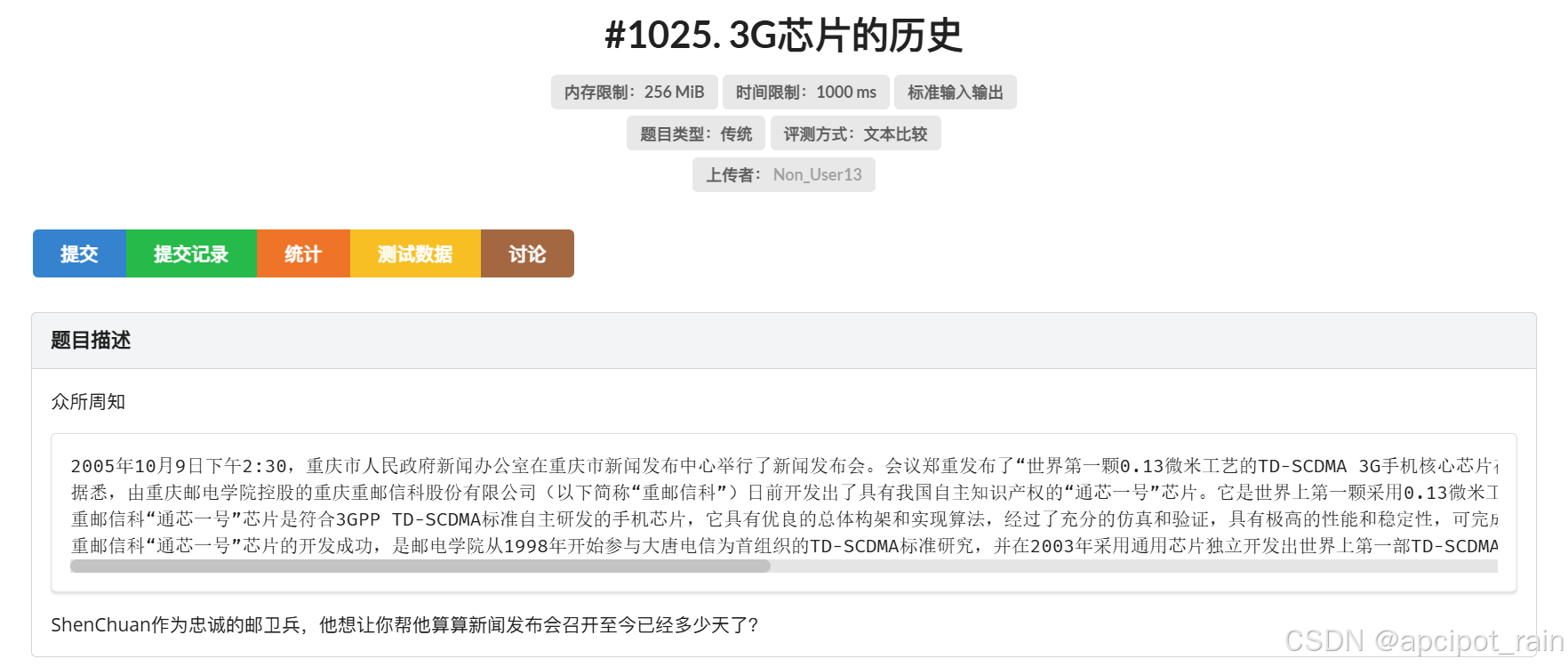
目录

不要老想着做难题,只要拿下基础题的分,你也没有及格。
——沃兹基硕德
T1(题目难度:1 知识难度:3)

审题
这题是经典的日历题。
本来是无脑暴力加都行,31+29+31+30+4=125
知识点1:日历
但是身为学生,我们有必要去复习日历的完整表达方式。
首先,小学口诀:一三五七八十腊,三十一天永不差。四六九冬三十天,平年二月二十八。
那么我们需要的是讨论2月的28天和29天。
可以开一个二维数组记录天数:
int month[2][13]={{0,31,28,31,30,31,30,31,31,30,31,30,31},
{0,31,29,31,30,31,30,31,31,30,31,30,31}};然后怎么判断闰年呢?年份能被4整除且不被100整除,或者,年份被400整除。
if((year%4==0&&year%100!=0)||year%400==0) days+=366;
else days+=365;最后一个难点:累计相加。
有人问相加有什么难的呀!
这是2000.1.1当然相对不难,但是如果是2000.2.2到2012.5.4,你怎么加呢?
我们先理一下思路:先把完整的年份加掉,然后再计算2012.1.1到2012.5.4的天数,加上去,最后是计算2000.2.2-2000.12.31的天数,加上去。
我们如果有优化的思维,那会更好办一些:2000.2.2到2000.12.31的天数=2000的天数-2000.1.1到2020.2.1的天数。
那么这就可以写一个函数,计算某年1月1日到某月某日的天数:
int add_days(int year,int month,int day)
{
int ans=0,flag=0;//ans是返回的天数结果,flag标记是否为闰年
if((year%4==0&&year%100!=0)||year%400==0) flag=1;//若为闰年,那么flag=1
for(int i=1;i<month;i++)//i需要小于month,因为如果是5月4号,那你不能把5月的31天也算进来
ans+=monthday[flag][i];//这就是设flag的妙处,提前解决了分类讨论的问题
ans+=day;
return ans;
}
讲解完毕,附赠一道课后作业(来源于我专的ACM平台,如侵则删):
T2(题目难度:5 知识难度:3)

题目数据:
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
16 64 16 64 34 68 127 126 66 -124 67 4 66 4 66 -124 126 100 66 36 66 4 66 4 66 4 126 4 66 40 0 16
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
0 -128 64 -128 48 -128 17 8 1 -4 2 8 8 80 16 64 32 64 -32 64 32 -96 32 -96 33 16 34 8 36 14 40 4
4 0 3 0 1 0 0 4 -1 -2 4 0 4 16 7 -8 4 16 4 16 4 16 8 16 8 16 16 16 32 -96 64 64
16 64 20 72 62 -4 73 32 5 16 1 0 63 -8 1 0 -1 -2 0 64 0 80 63 -8 8 64 4 64 1 64 0 -128
0 16 63 -8 1 0 1 0 1 0 1 4 -1 -2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 5 0 2 0
2 0 2 0 7 -16 8 32 24 64 37 -128 2 -128 12 -128 113 -4 2 8 12 16 18 32 33 -64 1 0 14 0 112 0
1 0 1 0 1 0 9 32 9 16 17 12 17 4 33 16 65 16 1 32 1 64 0 -128 1 0 2 0 12 0 112 0
0 0 0 0 7 -16 24 24 48 12 56 12 0 56 0 -32 0 -64 0 -128 0 0 0 0 1 -128 3 -64 1 -128 0 0 审题
这题的主要难度来自于:审题。
没错我读了半天题目。字节?有符号整数?字形?墨迹?
可能很多人读下来就已经放弃了。
但是打个比赛都没有耐心,那300r不是白交了?
重新审题,联系已经学过的知识:
“一个字节可以储存8位信息”,这句话是什么意思?
我们需要知道,在计算机中,数据是以二进制形式存储的。(不然这题确实做不了)
每个bit存储的数据非0即1,那么1bytes=8bit,一个字节可以存8个数据。
如果我们联想到2进制的换算,那么8个数据可以表示0-255。
但是这题,负数的数据是什么鬼??!
思路再调整:我一开始想到的是,第一个bit是存储正负值的,后面的数据就是纯数据值,可以表示-127到正127(而且正数和负数,除了最高位,都具有对称性)。但是我发现题目的-128是不是超纲了?如果是按我的方法来说,那么就需要9位单位存储。
知识点1:反码补码
思路再调整:嗯,我去问了下kimi(毕竟DS用不了一点),恍然大悟。

学艺不精啊!我把反码补码给忘完了。
这下我一下就明白了,这个就是反码补码的知识。
等效地说,就是你的负数加上256,就是二进制存储的数据。比如-4,在二进制中加上256,那么就是252的2进制:11111100。(我只是通俗地说这是“等效”形式,但是实际上的运算是每位取反再加1,不过学过二进制后就可以证明该运算的实质就是加256。)
那么调整反思一下,为什么我之前的方法表示不到-128,就是因为+0和-0会出现2种表示方式。
先人的智慧还是牛逼啊!
扯远了,回到题目上。每一个字就是用32个字节存储的,每一个字节有8个单位,如果这个单位是1,那么我们取'|'输出,如果单位是0,那么我们输出' '。例如:


有一种至拙至美的优雅。
知识点2:数转二进制
那么我们怎么实现从0-255的数字转换为2进制呢?我们以200举例
二进制转10进制是一个顺过程。那么我们现在分析逆过程:
那么200=100*2+0,100=50*2+0,50=25*2+0,25=12*2+1,12=6*2+0,6=3*2+0,3=1*2+1,
组合起来非常美丽啊:
这边我解释能力有限了(已老实求放过),放代码:
if(x<0) x=x+256;
int p=0;
while(p<8){
trans[i][j*8-p]=x%2;
x/=2;
p++;
}
//其中trans[16][16]是我把数字转二进制的数组,效果如上图。重复运行10次,那么我们得到:“九的九次方等于多少?”
cout<<(long long)pow(9,9);
T3(题目难度:4 知识难度:2)

审题
这题的题意相对来说很好读懂。
但是,显然,用longlong暴力乘是会炸的,除非你用高精度(我没试过)。
调整思路
我一开始想的是把每个数尾巴的数单独拎出来(%10),如果是0结果直接加1,如果不是0,那么就存进一个数组里,最后把他们相乘。
但是这种方法很快遭到了否定,如果是20和5,那么理论结果应该是2(100末尾2个0),但是我会跑出1(尾巴是0和5)。因此显然不能单纯用尾数字去处理。
再调整思路
那么我们得回到数字本身。根据上面的想法,启发一下,我在思考:什么数乘什么数结果会出现0?显然,2*5,4*5,6*5,8*5都会出现0。
我之前做过一些分解因数的题目,如果用分解思维来看,偶数乘5的本质还是落到2×5。
而对于10,其实本质上也还是能分解成2*5。
而其他情况,如3*7,4*6...永远不会出现0结尾的情况。
也就是说,对于任何两个数字相乘,只要不是2的倍数×5的倍数,最终结果都不是0结尾。
所以,兜兜转转最终找到了问题的切入口:把所有输入的数分解成若干个2、若干个5、和其它数的乘积,再把2的数量和5的数量累计起来(设为x,y),那么我们最终得到的min(x,y)就是0结尾的数字。比如7个2和3个5相乘,那么就是3个10和4个2相乘,4个2相乘结果尾数不是0,那么最终含0尾数只有3个。
代码如下:
#include<iostream>
using namespace std;
int x,count=0;
long long two=0,five=0;
int main()
{
for(int i=1;i<=10;i++){
for(int j=1;j<=10;j++){
cin>>x;
while(x%2==0){
x/=2;
two++;
}
while(x%5==0){
x/=5;
five++;
}
}
}
cout<<two<<' '<<five;
return 0;
}T7(题目难度:8 知识难度:6)
蓝桥杯网站的不太清晰,我在这放洛谷的图。


审题
这一题很显然是一个搜索题,用的是广度优先搜索(BFS)。
知识点1:BFS
关于BFS和算法实现,我打算单独开一个帖子讲。这里就默认你们知道BFS是啥啦。
思路
这题应该是原先几个小岛,后面有几个小岛,然后相减得到答案。
我的模拟思路是,开两个sea1 sea3数组(原本是sea2但是后面做了调整),0是海水,1是陆地。sea1是上升前,sea3一个是上升后,分别求这两个数组里有个小岛。
求小岛就是搜到一块陆地再去上下左右4个方向搜索。搜索每一个点都要把它变成海,搜完后count++,继续搜下一个陆地再BFS即可。
那么怎么模拟海平面上升呢?
如果原先这个点是一块临海陆地,临海的条件就是周围四个方向至少有一个是海洋。注意我们参照的是sea1,但是不能改动sea1,改掉的只能是sea3。
void drown()
{
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(sea1[i][j]!=0){//如果是一块陆地
for(int k=1;k<=4;k++){
if(i+dx[k]<=n&&i+dx[k]>=1&&j+dy[k]<=n&&j+dy[k]>=1&&sea1[i+dx[k]][j+dy[k]]==0){//如果周围是海
sea3[i][j]=0;
break;
}
}
}
}
}
return ;
}然后分别也用BFS统计sea1和sea2的小岛数量就可以啦!
再然后就完美地错了一堆点。。。
进去看了看洛谷大佬的解释:

这番话很一针见血,立马知道我的问题在哪了。
调整思路
岛屿可能由少变多,怎么办!
那么我们的标记是需要调整的。
因此我有了sea2和sea4数组——这样子下来其实会非常冗长麻烦,但是别问,问就是满分过了。
sea1是单纯模拟岛屿和海洋,岛屿1,海洋0;sea2就是岛屿有1234的标号了,海洋依旧是0。
sea3sea4逻辑同理。但是sea4的标号特殊:他不能单独标号,他如果是陆地,那么必须等于sea2的标号。(如果sea2是陆地,但sea4不是陆地,那么显然就是被淹掉了嘛!)不然,标号还是会越标越多。
统计sea2和sea4的标号数量,sea4的标号有多少是缺失了的,那就说明这个岛屿被完全淹没了。
Example:




图的顺序是sea1,sea2,sea3,sea4。我们看见sea4只剩下1,4,6,7,那么sea2的标号最大值7(7座岛屿)减去4就是最终答案。
bool res[1000]={0};//标号量
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
res[sea4[i][j]]=1;
}
}
for(int i=1;i<=ans1;i++){
if(res[i]!=0)
ans2++;
}
cout<<ans1-ans2;不放我的代码,因为这题做的实在是太冗长且重复了。。。
其他题
我没做出来!
没错,第七题都做出来了,但是5、6除了暴力就没想出别的算法,所以不写了。。。
总结
蓝桥杯满分150分,哎这不高中数学吗!
但是,题量只有8道,A了4题,喜提55。前两道填空就5分(痛苦面具)。
考试4个小时,还是要有一定策略,该放的放,只会暴力的就要最后来。
不要老想着钻难题,简单题该拿得分拿到来,跟高中数学一样。虽然简单题的分确实少!
如果一条思路不行,就调整思路。
人总是在不断地试错、调整、突破、再试错、再调整、再突破的循环中完成自我革命的!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








