负数的开方到底等于多少？

文：杨树森@知乎
编：小鹿鹿lulu

负数的开方到底等于多少?举个栗子

拿出小本本, 一通变换,得到:

Really? 且看下面详解

乘方来源于乘法，我们可以归纳地定义，设 是一个域， , 则

上述的域 可以是有理数域 , 实数域 , 或复数域 前两个不谈,可以将复数定义为

其中 然后定义复数的乘法

所谓的域，就是带有四则运算的集合。值得注意的是，除法作为乘法的逆运算，建立的前提是对于任意 , 当 时，存在唯一的 , 使得

从而可以把 定义为 .但是在开方运算中，是否存在唯一的 使得

是我们还没有验证的。

利用分析手段，我们知道在实数集中，设 , 则函数 , 当 是奇数时是双射，当 是偶数时值域是 且先减后增。

因此，可以定义 当 是奇数时为方程 的唯一解，当 是偶数时，若 则为方程 的唯一非负解，若 则不存在。

进一步地，可以将 看作是 将 看作是 利用

定义有理指数幂。

截止到目前，关于 我们已经得知当 或 时的值，以及当 , 且 的最简分数表示的分母为奇数时的值。

另外，当 时，可以将 上的函数 延拓为 上的连续函数。于是对于一切正数，它的任意实数次幂都有定义。这是高中数学的内容，看起来相当完善。

然而当 时的情况非常糟糕，因为已有定义的指数幂的结构很复杂。这体现出刚才定义的负数的指数幂是有缺陷的。

事实上，在实分析中，我们往往回避负数的非整数次幂，而在以 Mathematica 为代表的数学软件中，也不是像刚才那样定义的。

为了叙述新定义，首先引入指数函数

它是 上的函数。可以验证它有类似于前面的指数运算的性质

因此，记 ,然后记 ,另外，引入三角函数

于是对于任意

成立

请注意，指数函数和三角函数限制在 上都可以看作是实函数，且三角函数在 上有最小正周期，记为 , 如此定义的指数函数和三角函数，限制在 上和高中数学一致。

进一步地，指数函数限制在集合 上是单射，且值域为 对数函数 是指数函数在 上的反函数，于是

对数函数限制在 上是实函数，与高中数学一致。

习题：计算 和

对于任意 当 时，定义

当 时，定义

这就是复数的幂运算。回到开头的问题，得到

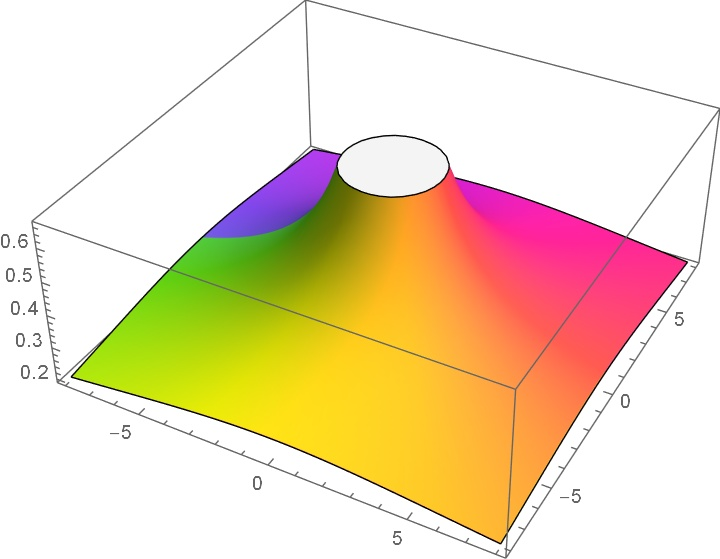
封面是函数 的图像。

最后我们解决复数的乘方和开方问题。根据指数函数和三角函数的性质，对于任意 当 时，存在唯一的 和 使得

这是复数的三角表示。在封面中，点的高度和颜色就是利用三角表示给出的。设 则

如此，再来观察负数的开方。设 , 则

这说明

以上对于复数的开方给出了两个不同的定义，其中第二个有更好的分析和代数性质。为什么会出现两个不同的定义？第二个定义好在哪里呢？

我们从复数的角度考虑方程 虽然按照刚才的定义，复数的三角表示是唯一的，但是如果允许 那么根据三角函数的周期性，上述的表示不再是唯一的。

事实上，关于 的方程 当 时有 个解。记 的三角表示为 则

在第一个开方定义中，记 则当 时使用的是第 个解，当 时使用的是第 个解。而在第二个开方定义中，使用的始终是第 个解，这也使得函数 在负实轴沿上方连续。

后台回复关键词【入群】

加入卖萌屋NLP/IR/Rec与求职讨论群

后台回复关键词【顶会】

获取ACL、CIKM等各大顶会论文集！