代码随想录算法训练营第五十二天 | 101.孤岛的总面积、102.沉没孤岛、103.水流问题、104.建造最大岛屿

102. 沉没孤岛

1、题目

题目描述：

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。

现在你需要将所有孤岛“沉没”，即将孤岛中的所有陆地单元格（1）转变为水域单元格（0）。

输入描述：

第一行包含两个整数 N, M，表示矩阵的行数和列数。

之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述

输出将孤岛“沉没”之后的岛屿矩阵。

输入示例：

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出示例：

1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1

提示信息：

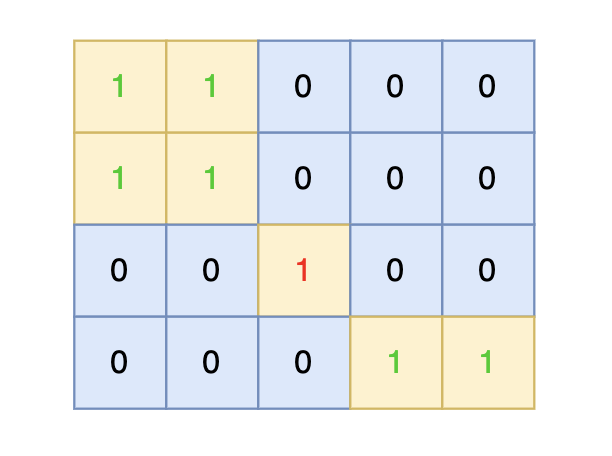
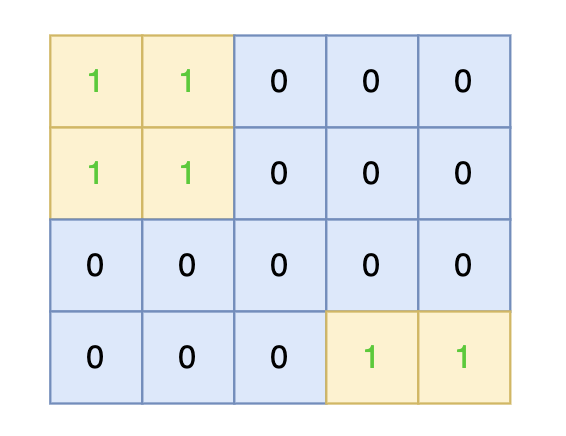
将孤岛沉没：

数据范围：

1 <= M, N <= 50

2、题解

这道题目和 101.孤岛的总面积 正好反过来了，101.孤岛的总面积是求 地图中间的空格数，而本题是要把地图中间的 1 都改成 0 。

那么两题在思路上也是差不多的。

思路依然是从地图周边出发，将周边空格相邻的陆地都做上标记，然后在遍历一遍地图，遇到 陆地 且没做过标记的，那么都是地图中间的 陆地 ，全部改成水域就行。

有的人可能想，我在定义一个 visited 二维数组，单独标记周边的陆地，然后遍历地图的时候同时对 数组board 和 数组visited 进行判断，决定 陆地是否变成水域。

这样做其实就有点麻烦了，不用额外定义空间了，标记周边的陆地，可以直接改陆地为其他特殊值作为标记。

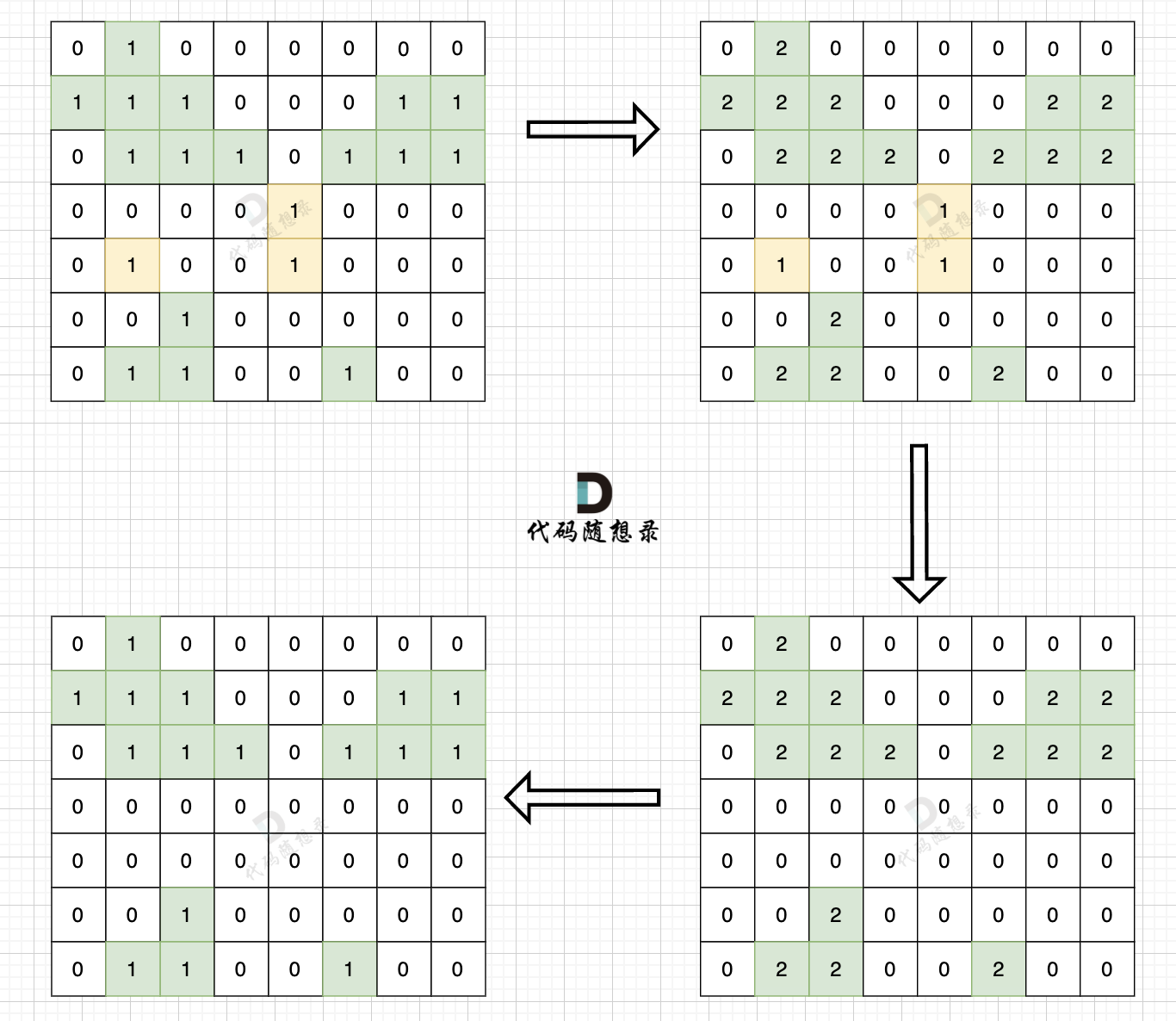
步骤一：深搜或者广搜将地图周边的 1 （陆地）全部改成 2 （特殊标记）

步骤二：将水域中间 1 （陆地）全部改成 水域（0）

步骤三：将之前标记的 2 改为 1 （陆地）

如图：

整体C++代码如下，以下使用dfs实现，其实遍历方式dfs，bfs都是可以的。

#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
void dfs(vector<vector<int>>& grid, int x, int y) {
    grid[x][y] = 2;
    for (int i = 0; i < 4; i++) { // 向四个方向遍历
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        // 超过边界
        if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
        // 不符合条件，不继续遍历
        if (grid[nextx][nexty] == 0 || grid[nextx][nexty] == 2) continue;
        dfs (grid, nextx, nexty);
    }
    return;
}

int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }

    // 步骤一：
    // 从左侧边，和右侧边 向中间遍历
    for (int i = 0; i < n; i++) {
        if (grid[i][0] == 1) dfs(grid, i, 0);
        if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
    }

    // 从上边和下边 向中间遍历
    for (int j = 0; j < m; j++) {
        if (grid[0][j] == 1) dfs(grid, 0, j);
        if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
    }
    // 步骤二、步骤三
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 1) grid[i][j] = 0;
            if (grid[i][j] == 2) grid[i][j] = 1;
        }
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cout << grid[i][j] << " ";
        }
        cout << endl;
    }
}

103. 水流问题

1、题目

题目描述：

现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。

矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

输入描述：

第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。

后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。

输出描述：

输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。

输入示例：

5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1

输出示例：

0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1

提示信息：

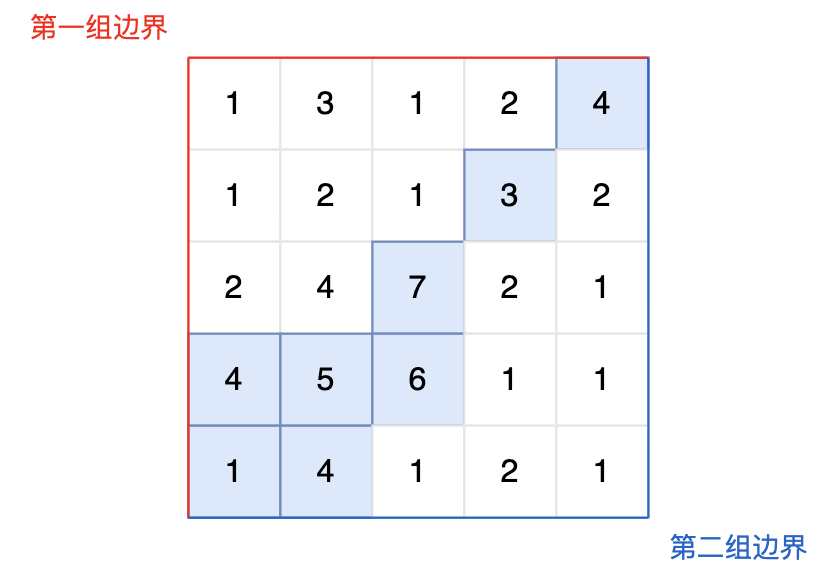
图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。

数据范围：

1 <= M, N <= 50

2、题解

一个比较直白的想法，其实就是 遍历每个点，然后看这个点 能不能同时到达第一组边界和第二组边界。

至于遍历方式，可以用dfs，也可以用bfs，以下用dfs来举例。

那么这种思路的实现代码如下：

#include <iostream>
#include <vector>
using namespace std;
int n, m;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};

// 从 x，y 出发 把可以走的地方都标记上
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
    if (visited[x][y]) return;

    visited[x][y] = true;

    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
        if (grid[x][y] < grid[nextx][nexty]) continue; // 高度不合适

        dfs (grid, visited, nextx, nexty);
    }
    return;
}
bool isResult(vector<vector<int>>& grid, int x, int y) {
    vector<vector<bool>> visited(n, vector<bool>(m, false));

    // 深搜，将x,y出发 能到的节点都标记上。
    dfs(grid, visited, x, y);
    bool isFirst = false;
    bool isSecond = false;

    // 以下就是判断x，y出发，是否到达第一组边界和第二组边界
    // 第一边界的上边
    for (int j = 0; j < m; j++) {
        if (visited[0][j]) {
            isFirst = true;
            break;
        }
    }
    // 第一边界的左边
    for (int i = 0; i < n; i++) {
        if (visited[i][0]) {
            isFirst = true;
            break;
        }
    }
    // 第二边界右边
    for (int j = 0; j < m; j++) {
        if (visited[n - 1][j]) {
            isSecond = true;
            break;
        }
    }
    // 第二边界下边
    for (int i = 0; i < n; i++) {
        if (visited[i][m - 1]) {
            isSecond = true;
            break;
        }
    }
    if (isFirst && isSecond) return true;
    return false;
}


int main() {
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    // 遍历每一个点，看是否能同时到达第一组边界和第二组边界
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (isResult(grid, i, j)) {
                cout << i << " " << j << endl;
            }
        }
    }
}

这种思路很直白，但很明显，以上代码超时了。 来看看时间复杂度。

遍历每一个节点，是 m * n，遍历每一个节点的时候，都要做深搜，深搜的时间复杂度是： m * n

那么整体时间复杂度 就是 O(m^2 * n^2) ，这是一个四次方的时间复杂度。

优化

那么我们可以 反过来想，从第一组边界上的节点 逆流而上，将遍历过的节点都标记上。

同样从第二组边界的边上节点 逆流而上，将遍历过的节点也标记上。

然后两方都标记过的节点就是既可以流太平洋也可以流大西洋的节点。

从第一组边界边上节点出发，如图：

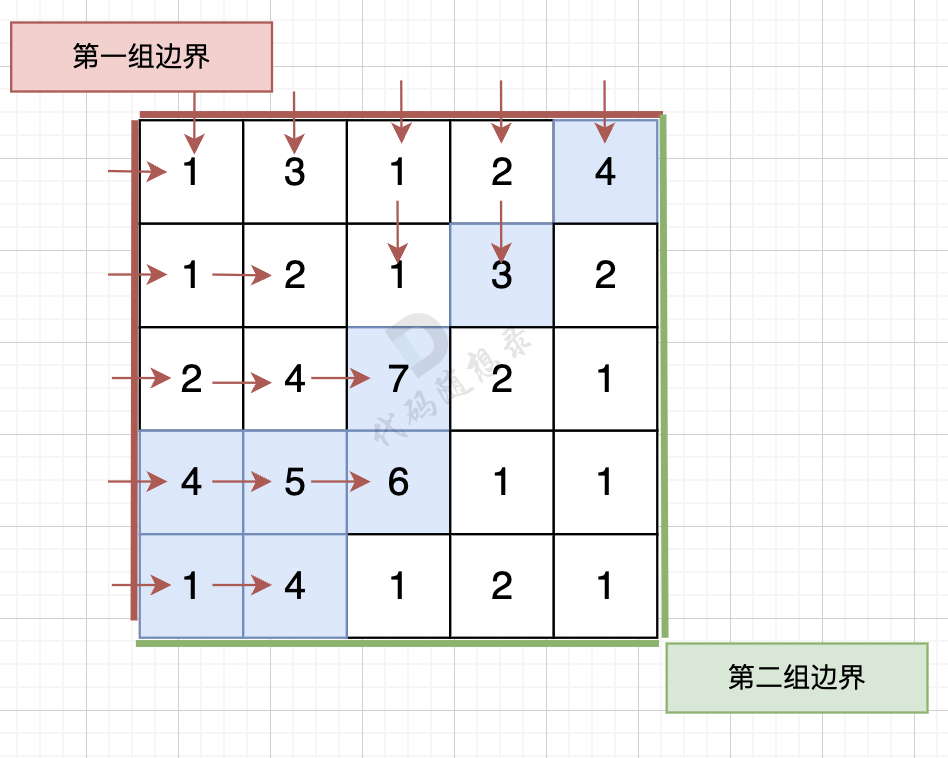
从第二组边界上节点出发，如图：

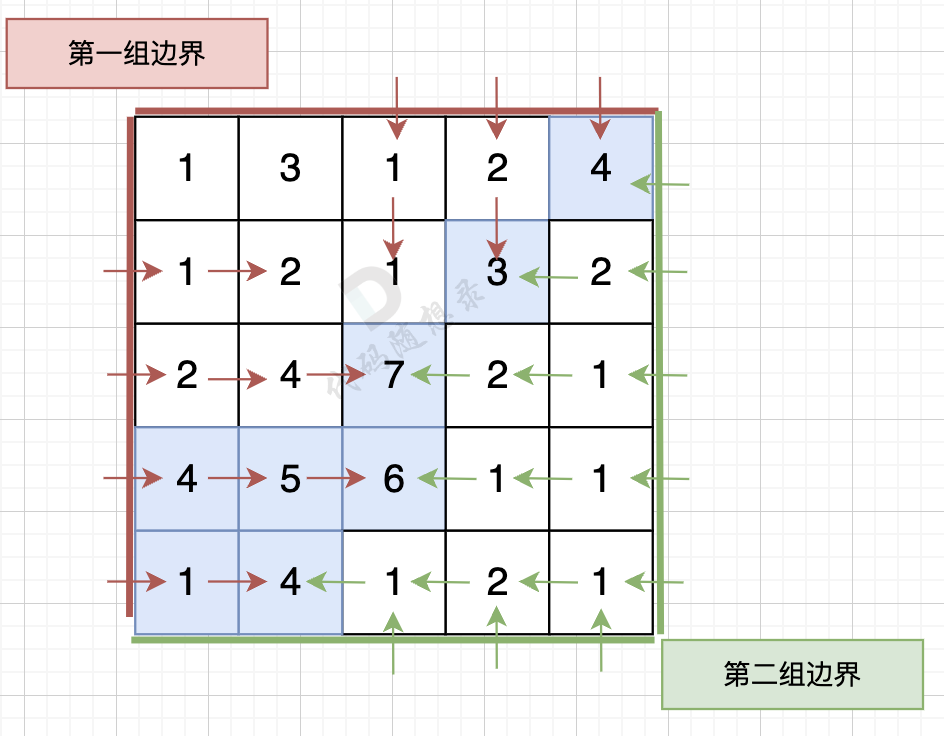
按照这样的逻辑，就可以写出如下遍历代码：（详细注释）

#include <iostream>
#include <vector>
using namespace std;
int n, m;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
    if (visited[x][y]) return;

    visited[x][y] = true;

    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
        if (grid[x][y] > grid[nextx][nexty]) continue; // 注意：这里是从低向高遍历

        dfs (grid, visited, nextx, nexty);
    }
    return;
}



int main() {

    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    // 标记从第一组边界上的节点出发，可以遍历的节点
    vector<vector<bool>> firstBorder(n, vector<bool>(m, false));

    // 标记从第一组边界上的节点出发，可以遍历的节点
    vector<vector<bool>> secondBorder(n, vector<bool>(m, false));

    // 从最上和最下行的节点出发，向高处遍历
    for (int i = 0; i < n; i++) {
        dfs (grid, firstBorder, i, 0); // 遍历最左列，接触第一组边界
        dfs (grid, secondBorder, i, m - 1); // 遍历最右列，接触第二组边界
    }

    // 从最左和最右列的节点出发，向高处遍历
    for (int j = 0; j < m; j++) {
        dfs (grid, firstBorder, 0, j); // 遍历最上行，接触第一组边界
        dfs (grid, secondBorder, n - 1, j); // 遍历最下行，接触第二组边界
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            // 如果这个节点，从第一组边界和第二组边界出发都遍历过，就是结果
            if (firstBorder[i][j] && secondBorder[i][j]) cout << i << " " << j << endl;;
        }
    }


}

时间复杂度分析， 关于dfs函数搜索的过程 时间复杂度是 O(n * m)，这个大家比较容易想。

关键看主函数，那么每次dfs的时候，上面还是有for循环的。

第一个for循环，时间复杂度是：n * (n * m) 。

第二个for循环，时间复杂度是：m * (n * m)。

所以本题看起来 时间复杂度好像是 ： n * (n * m) + m * (n * m) = (m * n) * (m + n) 。

其实这是一个误区，大家再自己看 dfs函数的实现，其实 有visited函数记录 走过的节点，而走过的节点是不会再走第二次的。

所以 调用dfs函数，只要参数传入的是 数组 firstBorder，那么地图中 每一个节点其实就遍历一次，无论你调用多少次。

同理，调用dfs函数，只要 参数传入的是 数组 secondBorder，地图中每个节点也只会遍历一次。

所以，以下这段代码的时间复杂度是 2 * n * m。 地图用每个节点就遍历了两次，参数传入 firstBorder 的时候遍历一次，参数传入 secondBorder 的时候遍历一次。

// 从最上和最下行的节点出发，向高处遍历
for (int i = 0; i < n; i++) {
    dfs (grid, firstBorder, i, 0); // 遍历最左列，接触第一组边界
    dfs (grid, secondBorder, i, m - 1); // 遍历最右列，接触第二组边界
}

// 从最左和最右列的节点出发，向高处遍历
for (int j = 0; j < m; j++) {
    dfs (grid, firstBorder, 0, j); // 遍历最上行，接触第一组边界
    dfs (grid, secondBorder, n - 1, j); // 遍历最下行，接触第二组边界
}

那么本题整体的时间复杂度其实是： 2 * n * m + n * m ，所以最终时间复杂度为 O(n * m) 。

空间复杂度为：O(n * m) 这个就不难理解了。开了几个 n * m 的数组。

104.建造最大岛屿

1、题目

题目描述：

给定一个由 1（陆地）和 0（水）组成的矩阵，你最多可以将矩阵中的一格水变为一块陆地，在执行了此操作之后，矩阵中最大的岛屿面积是多少。

岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。

输入描述：

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述：

输出一个整数，表示最大的岛屿面积。

输入示例：

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出示例

6

提示信息

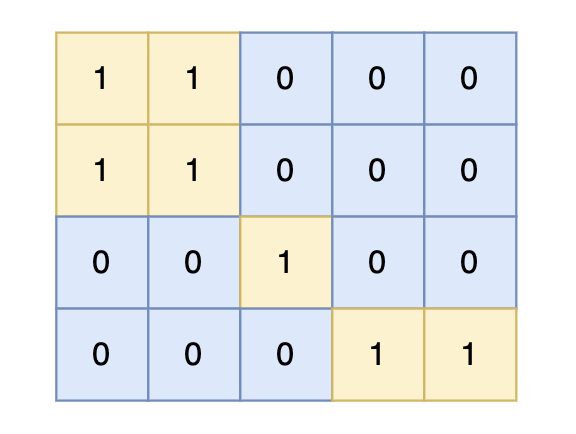
对于上面的案例，有两个位置可将 0 变成 1，使得岛屿的面积最大，即 6。

数据范围：

1 <= M, N <= 50。

2、题解

本题的一个暴力想法，应该是遍历地图尝试 将每一个 0 改成1，然后去搜索地图中的最大的岛屿面积。

计算地图的最大面积：遍历地图 + 深搜岛屿，时间复杂度为 n * n。

（其实使用深搜还是广搜都是可以的，其目的就是遍历岛屿做一个标记，相当于染色，那么使用哪个遍历方式都行，以下我用深搜来讲解）

每改变一个0的方格，都需要重新计算一个地图的最大面积，所以 整体时间复杂度为：n^4。

优化思路

其实每次深搜遍历计算最大岛屿面积，我们都做了很多重复的工作。

只要用一次深搜把每个岛屿的面积记录下来就好。

第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积

第二步：再遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。

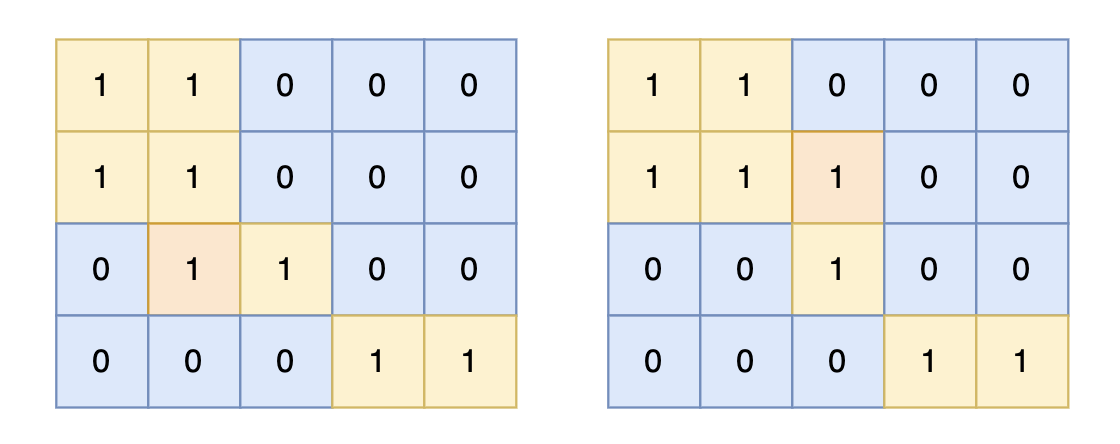
拿如下地图的岛屿情况来举例： （1为陆地）

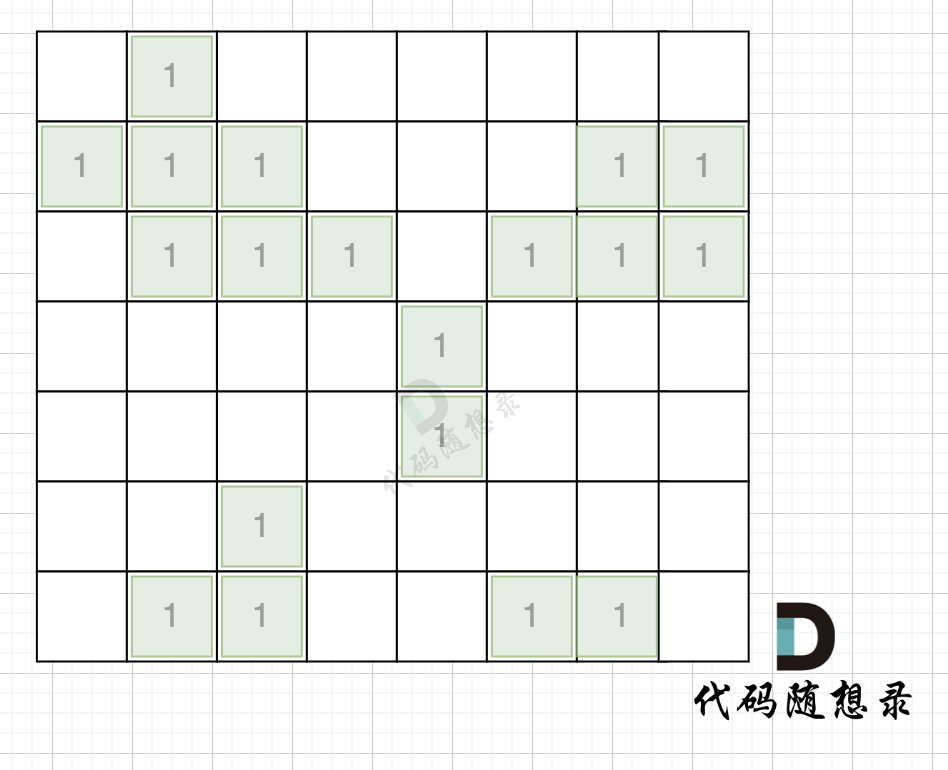
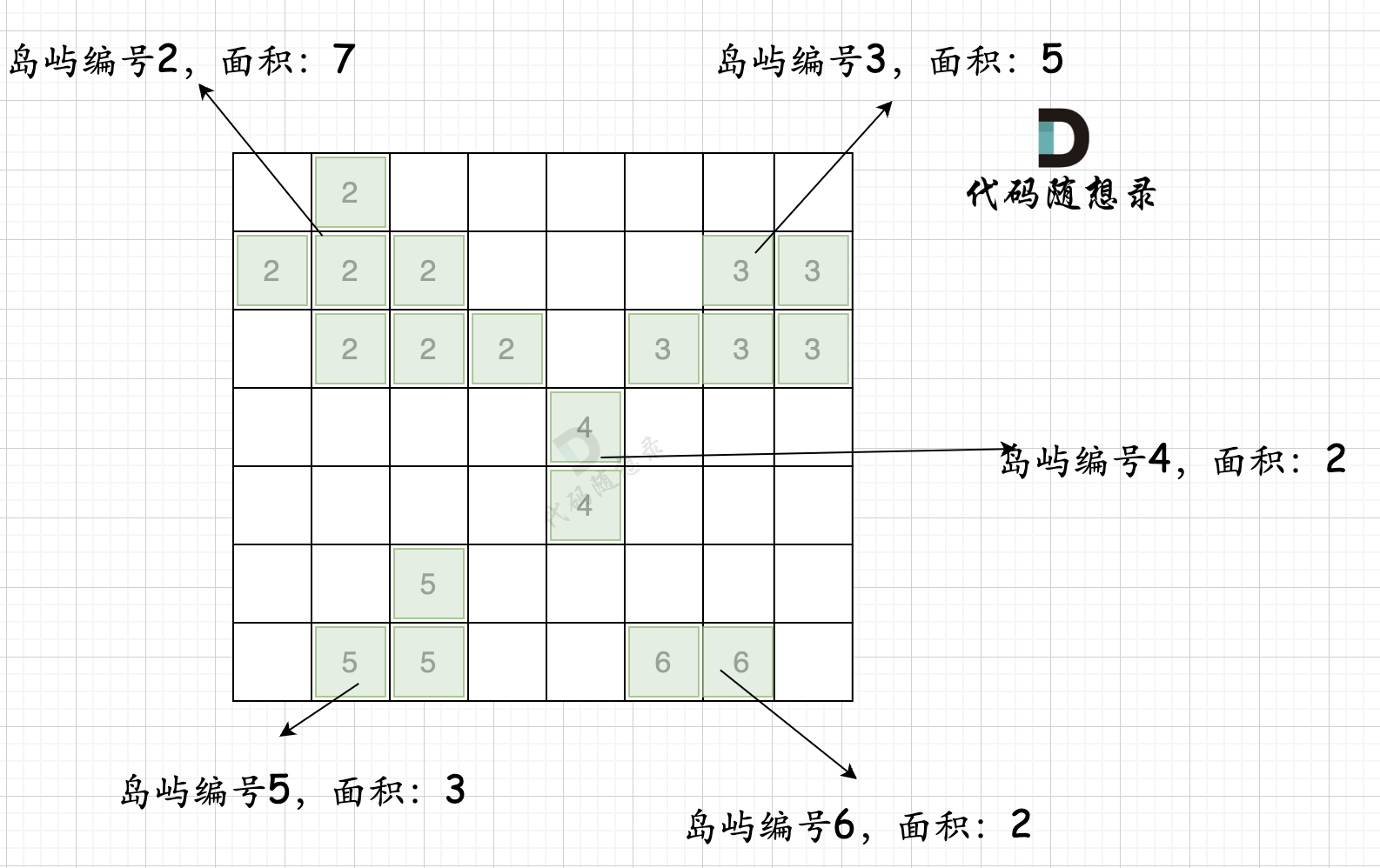
第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示：

第二步过程如图所示：

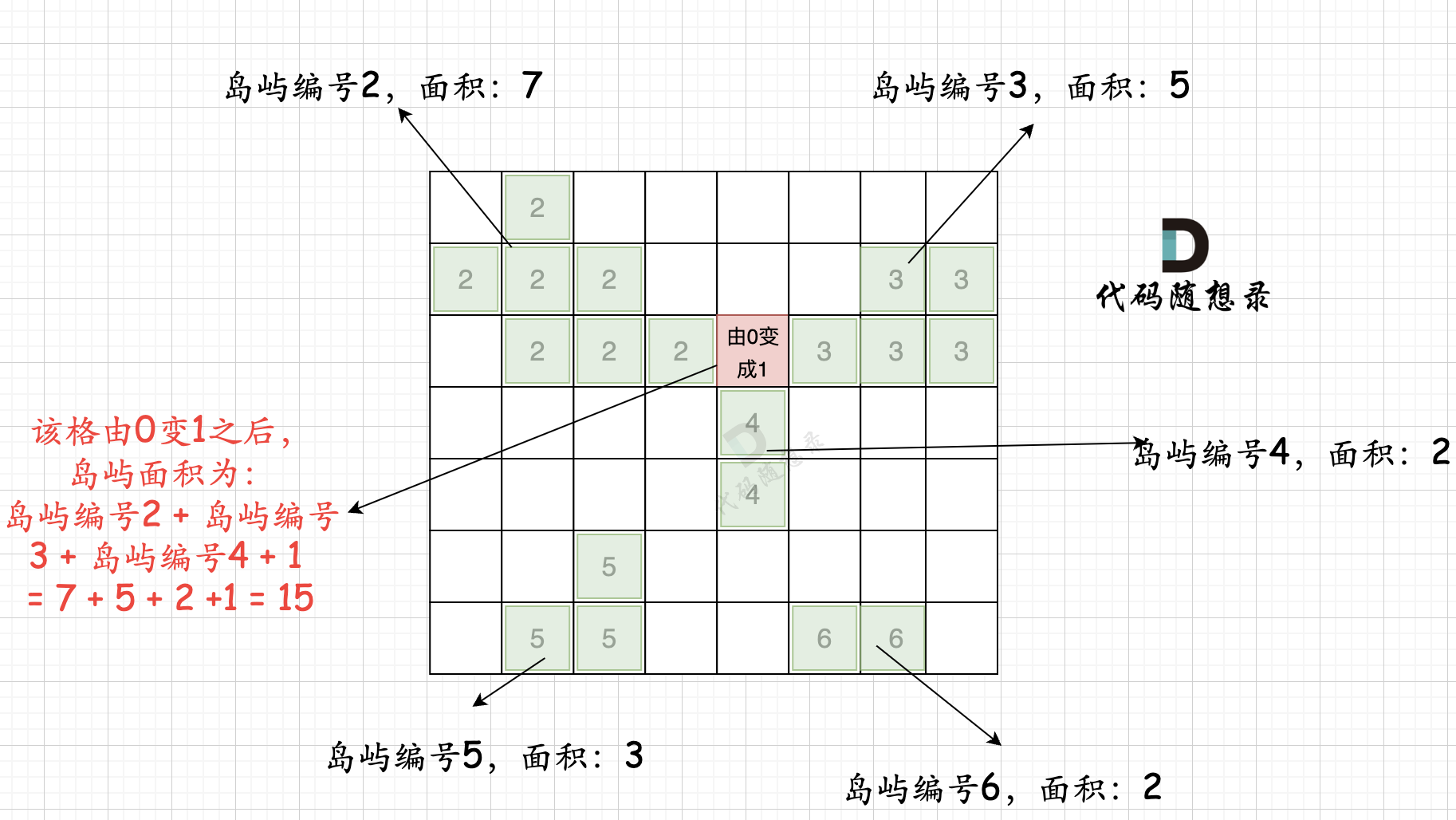
也就是遍历每一个0的方格，并统计其相邻岛屿面积，最后取一个最大值。

这个过程的时间复杂度也为 n * n。

所以整个解法的时间复杂度，为 n * n + n * n 也就是 n^2。

当然这里还有一个优化的点，就是 可以不用 visited数组，因为有mark来标记，所以遍历过的grid[i][j]是不等于1的。

整体代码如下：

#include <iostream>
#include <vector>
#include <unordered_set>
#include <unordered_map>
using namespace std;
int n, m;
int count;

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int mark) {
    if (visited[x][y] || grid[x][y] == 0) return; // 终止条件：访问过的节点 或者 遇到海水
    visited[x][y] = true; // 标记访问过
    grid[x][y] = mark; // 给陆地标记新标签
    count++;
    for (int i = 0; i < 4; i++) {
        int nextx = x + dir[i][0];
        int nexty = y + dir[i][1];
        if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;  // 越界了，直接跳过
        dfs(grid, visited, nextx, nexty, mark);
    }
}

int main() {
    cin >> n >> m;
    vector<vector<int>> grid(n, vector<int>(m, 0));

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> grid[i][j];
        }
    }
    vector<vector<bool>> visited(n, vector<bool>(m, false)); // 标记访问过的点
    unordered_map<int ,int> gridNum;
    int mark = 2; // 记录每个岛屿的编号
    bool isAllGrid = true; // 标记是否整个地图都是陆地
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            if (grid[i][j] == 0) isAllGrid = false;
            if (!visited[i][j] && grid[i][j] == 1) {
                count = 0;
                dfs(grid, visited, i, j, mark); // 将与其链接的陆地都标记上 true
                gridNum[mark] = count; // 记录每一个岛屿的面积
                mark++; // 记录下一个岛屿编号
            }
        }
    }
    if (isAllGrid) {
        cout << n * m << endl; // 如果都是陆地，返回全面积
        return 0; // 结束程序
    }

    // 以下逻辑是根据添加陆地的位置，计算周边岛屿面积之和
    int result = 0; // 记录最后结果
    unordered_set<int> visitedGrid; // 标记访问过的岛屿
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            count = 1; // 记录连接之后的岛屿数量
            visitedGrid.clear(); // 每次使用时，清空
            if (grid[i][j] == 0) {
                for (int k = 0; k < 4; k++) {
                    int neari = i + dir[k][1]; // 计算相邻坐标
                    int nearj = j + dir[k][0];
                    if (neari < 0 || neari >= n || nearj < 0 || nearj >= m) continue;
                    if (visitedGrid.count(grid[neari][nearj])) continue; // 添加过的岛屿不要重复添加
                    // 把相邻四面的岛屿数量加起来
                    count += gridNum[grid[neari][nearj]];
                    visitedGrid.insert(grid[neari][nearj]); // 标记该岛屿已经添加过
                }
            }
            result = max(result, count);
        }
    }
    cout << result << endl;

}