引言
这篇文章是对 Multivariable Calculus 课程的知识点总结。
Dot Product
Because the dot product results in a scalar, it is also called the scalar product.
algebraic view of dot product
给定两个向量 a⃗ =⟨a1,a2,a3⟩ , b⃗ =⟨b1,b2,b3⟩ ,它们的点积定义如下:
properties of dot product
下面属性的证明大部分都是一些代数计算,根据点积的 algebraic view,你可以很轻松地证明出来。
geometric view of dot product
下面定理用 The Law of Cosines 来证明,详细步骤参考:Dot Product
这个公式通常不是用来计算点积,而是找出2个向量之间的角。有了这个公式,点积可以让我们很容易地判断出2个向量是否 perpendicular or parallel. (When two vectors are perpendicular to each other we say they are orthogonal.)
Now, if two vectors are orthogonal then we know that the angle between them is 90 degrees:
Likewise, if two vectors are parallel then the angle between them is either 0 degrees (pointing in the same direction) or 180 degrees (pointing in the opposite direction):
Projections
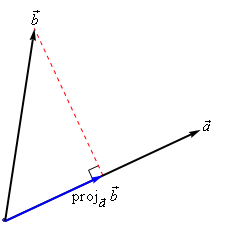
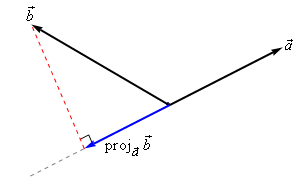
下面2幅图是 the projection of b⃗ onto a⃗ , denoted by proja⃗ b⃗
There is an nice formula for finding the projection of b⃗ onto a⃗ . Here it is,
Note that we also need to be very careful with notation here. The projection of a⃗ onto b⃗ is given by:
Cross Product
We should note that the cross product requires both of the vectors to be three dimensional vectors. The result of a dot product is a number and the result of a cross product is a vector!
Area and Determinants
下图中是第一种求三角形面积的方式。
我们知道点积中的公式是 cosθ ,而上图中是 sinθ ,那么如何转化一下它们呢?下图中的方法实现了转化,图中错误的部分我用红线标出了。它的主要思想如下:
1、把向量 A⃗ 旋转90度,因此得到了 sinθ=cosθ′
2、由于是旋转,所以向量 A⃗ 的长度不变
3、通过旋转,我们得到了 A′,θ′,B ,可以应用点积公式了
上图中的最终结果实际上就是 a1b2−a2b1=det(A⃗ ,B⃗ )=∣∣∣a1b1a2b2∣∣∣ ,如果你想用 determinant 求面积,你需要加上绝对值,由于面积始终为正的。还有一点就是,determinant 的绝对值是平行四边形的面积,三角形应该乘以1/2
cross product 的定义
下图中是2个向量的 cross product 的定义:
下图中是关于 cross product 的方向与长度的定理:
关于 cross product 还有2个知识点:
1、 A⃗ ×B⃗ =−(B⃗ ×A⃗ )
2、根据1,可得 A⃗ ×A⃗ =0
Volumes and Determinants
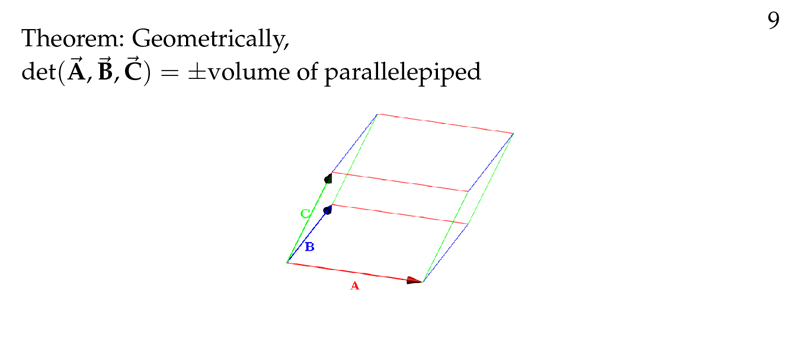
determinant 同样可以求体积:
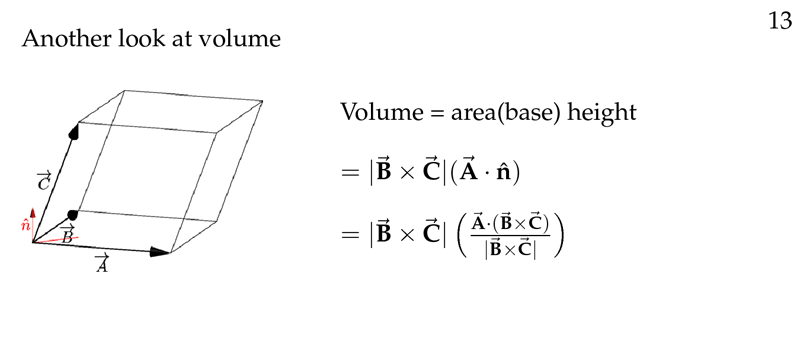
下图中是用另一种方法来求体积,如果你一直算下去,你会发现它实际上就是 determinant,即: A⃗ ⋅(B⃗ ×C⃗ )=det(A⃗ ,B⃗ ,C⃗ )
Equations of Planes
如下图所示,已知平面上的3个点,求出表示平面的方程。在上面我们已经知道 determinant 可以求体积,而平面的体积为0,所以有下图中的公式求平面方程。
我们还用上面的图形,第二种方式求解方式: P1P→⋅(P1P2→×P1P3→)=0 ,你会发现它实际上就是 determinant
一个平面的公式形式为: ax+by+cz=d ,当我们知道了一个平面的 normal vector 以后,就可以确定无数多个平行的平面,如果再给出平面经过哪个点以后,就可以确定一个具体的平面了。
下图是一个具体的例子,它的 normal vector 为 N⃗ =⟨1,5,10⟩ ,并且通过 P0=(2,1,−1) ,用点积就可以求出平面的方程了。








 本文详细总结了MIT的18.02多变量微积分课程,涵盖点积的代数和几何观点、投影、叉积、平面方程、线性系统、二阶导数判别法、全微分与链式法则、梯度与方向导数、拉格朗日乘子法等内容,深入探讨了向量、平面、体积、约束条件下的最优化问题等核心概念。
本文详细总结了MIT的18.02多变量微积分课程,涵盖点积的代数和几何观点、投影、叉积、平面方程、线性系统、二阶导数判别法、全微分与链式法则、梯度与方向导数、拉格朗日乘子法等内容,深入探讨了向量、平面、体积、约束条件下的最优化问题等核心概念。

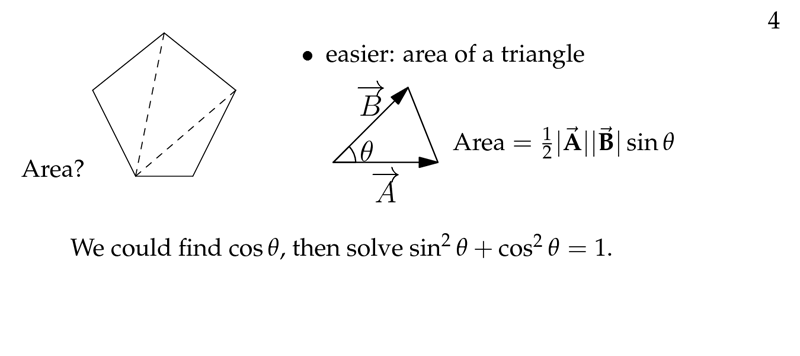
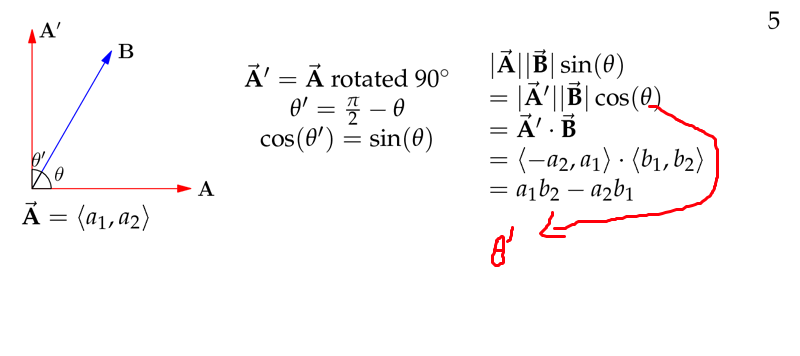




 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 4542
4542

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








