引言
这篇文章是对 MIT Single Variable Calculus 这个课程的知识点总结。在这个课程中,我遇到一些问题涉及到先前高中学过的知识,同时也有一些比较难理解的或容易混淆的概念,因此我把找到的这些资料链接列在下面(这些资料弥补了我先前忘记的知识,并且加深了对课程内容的理解,非常有帮助):
What is a Function?
Even and Odd Functions
Function Transformations
Inverse function
In what sense is the derivative the “best” linear approximation?
Inflection points introduction
Continuous versus differentiable
How to Detrmine when Limits Don’t Exist
Prove that the derivative of an even differentiable function is odd, and the derivative of an odd is even
limit and continuity
下面是 continuous 的定义:
A function f is continuous at
x0 if limx→x0f(x)=f(x0)
如果一个函数在 x0 处是 continuous 的,那么从下面的定义中,我们可以得出以下3个属性:
- limx→x+0f(x)=limx→x−0f(x)
- f(x0) is defined
- limx→x+0f(x)=limx→x−0f(x)=f(x0)
下面中的链接是关于 limit 的一些属性,和证明这些属性为什么是正确的。
下面我们来证明一个定理,定理的内容如下:
If f is differentiable at
x0 , then f is continuous atx0
如果 f is continuous at
sin 与 cos 导数的证明
在这个 lecture 中,David Jerison 教授讲解了 sin 与 cos 函数导数的代数与几何证明,在具体证明之前,让我们首先求出2个极限的解,它们分别是:
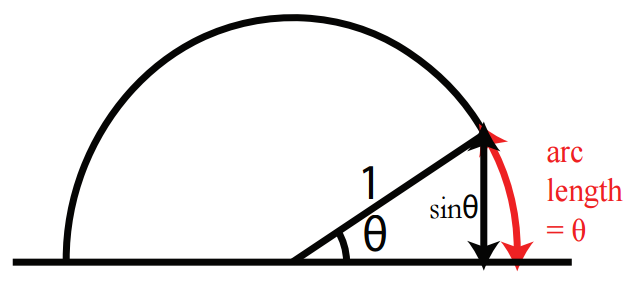
我们首先来证明第2个极限,下图是个单位圆,角度 θ is described in radians but NOT when it is measured in degrees.
把第2个极限中的 Δx 用 θ 替换,我们可以看出当 θ 无限接近于0时, sinθ 与 arc length(即 θ )无限接近,因此我们可以总结出:
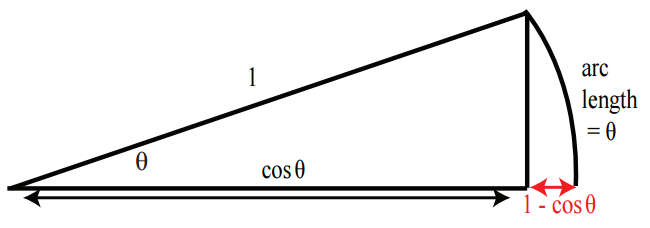
接下来让我们来求第1个极限,下图来自于单位圆的一部分,我们可以看出当 θ 无限接近于0时, 1−cosθ 无限接近接近于0,因此我们可以总结出:
上面的几何证明过程中,有2个重点我需要解释一下:
1、在MIT的课堂上,我看到很多同学会问到:当 θ 无限接近于0时, 1−cosθ 无限接近接近于0,同时 arc length 不也接近于0吗?这里我们忽略了一个重点,就是 1−cosθ 接近于0的速度要比 theta 接近于0的速度快很多。
2、上面极限中的角度全是以弧度来描述的,如果你以度数来描述,则上面的结论不成立,因此当我们对 sinx和cosx 求导时,这些 x 所指的一定要是弧度。
至此,我们已经求出了上面的2个极限。现在,只需要一些代数 tricks 就可以证明出
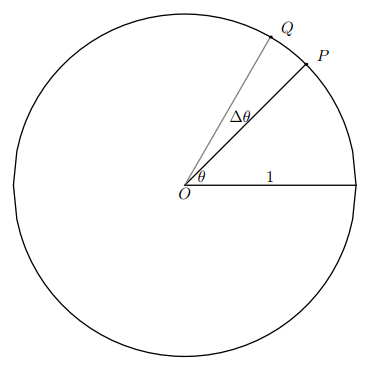
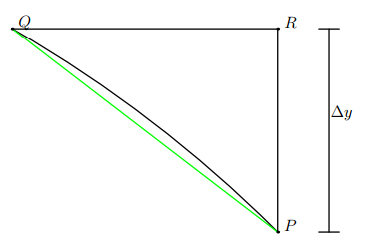
下面我们来用几何的方式去证明 sinx 的导数,导数本身想表达的就是 the rate of change,即 ratio,现在我们来看一看 y=sinθ ,当 θ 增加 Δθ 时, Δy 是多少?
下图是个单位圆,当角度增加 Δθ 时, y 如何变化呢?我们可以把上图中的弧
当 Δθ 无限小时,我们可以把弧 PQ 近似成上图的绿线,由于 Δθ = 弧 PQ ,所以直线 QP 约等于 Δθ ,现在最重要的就是我们要如何求出角 ∠QPR ,其实它就是 θ ,因此我们可以得出:
General Strategy for Curve Sketching
在这个 lecture 中, Jerison 教授介绍了一个通用的策略去大致描绘出函数图像,下面的链接中给出了具体的步骤,如果步骤1和2中的点很难找出,你可以直接跳到第3步。
函数的平均值
想必你已经知道如何求解一个离散集合的平均值,比如: a1,a2,…,an ,那么它的平均值定义如下:
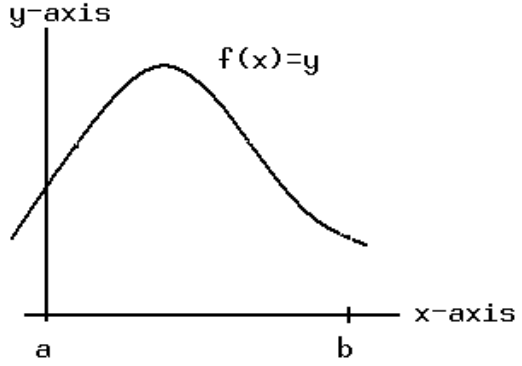
那么现在,我想求出下图中函数在区间 [a,b] 的平均值,我们怎样做到这点呢?
我们目前虽然不知道如何去求连续函数在某一区间的平均值,但是我们会求一个离散集合的平均值,因此我们可以通过这个方法来粗略估计出上图所示函数的平均值,过程如下:
1、Split [a,b] into subintervals width Δx=b−an
2、Pick a point xi in each subinterval
3、Average just the f(xi) :
随着 n 逐渐增大,上面估算出的平均值将会越接近真正的平均值,感觉有点像积分呢!别要着急,好戏还在后面。
4、把上面的公式中的分子与分母都乖上








 本文详述了MIT单变量微积分课程的重点,包括极限、连续性、导数证明、曲线拟合策略、函数平均值、积分求体积方法(盘方法、环方法、壳方法)、考试题目解析、积分求解技巧、洛必达法则、级数收敛性测试、幂级数和泰勒级数。内容深入浅出,适合微积分学习者参考。
本文详述了MIT单变量微积分课程的重点,包括极限、连续性、导数证明、曲线拟合策略、函数平均值、积分求体积方法(盘方法、环方法、壳方法)、考试题目解析、积分求解技巧、洛必达法则、级数收敛性测试、幂级数和泰勒级数。内容深入浅出,适合微积分学习者参考。
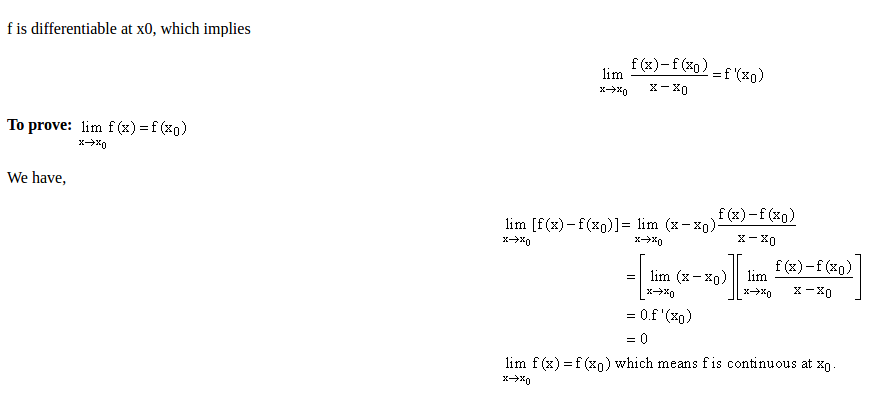
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1445
1445

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








