之前我写过《我对说话人识别/声纹识别的研究综述》,本篇基本上可以是这个综述的续写。其实,写的也没有什么深度,想获得深度信息的朋友们可以不用往下看了,还不如下载几篇领域内的国内博士论文看看。为什么是国内呢?因为国内博士论文前面的综述写的还不错,嘿嘿~我写这个主要是给不熟悉这个领域内的朋友看的,用通熟的话描述这个领域内重要的一些算法,等于是入个门吧。
PLDA算法
前面博客已经提到过声纹识别的信道补偿算法,而且重点说了LDA算法。PLDA(Probabilistic Linear Discriminant Analysis)也是一种信道补偿算法,号称概率形式的LDA算法。PLDA同样通常是基于I-vector特征的,因为I-vector特征即包含说话人信息又包含信道信息,而我们只关心说话人信息,所以才需要信道补偿。PLDA算法的信道补偿能力比LDA更好,已经成为目前最好的信道补偿算法。
关于PLDA的经典论文是这一篇《Probabilistic Linear Discriminant Analysis for Inferences About Identity》。可是,用了这个算法这么久,我一直搞不清楚为什么PLDA是概率形式的LDA。汗。。所以本文的写作思路也围绕这个问题的解决而展开。
在这篇论文中,作者说:PLDA与LDA的关系就好比因子分析和主成分分析PCA的关系。所以,我们有必要先简单提一下因子分析。
因子分析
因子分析 (factor analysis) 是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系,探求观测数据中的基本结构,并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量,而假想变量是不可观测的潜在变量,称为因子。
下面从网上摘抄一个因子分析的例子,感谢原作者!

PLDA算法解释
概念理解
在声纹识别领域中,我们假设训练数据语音由I个说话人的语音组成,其中每个说话人有J段自己不同的语音。那么,我们定义第i个说话人的第j条语音为Xij。然后,根据因子分析,我们定义Xij的生成模型为:
这个模型可以看成两个部分:等号右边前两项只跟说话人有关而跟说话人的具体某一条语音无关,称为信号部分,这描述了说话人类间的差异;等号右边后两项描述了同一说话人的不同语音之间的差异,称为噪音部分。这样,我们用了这样两个假想变量来描述一条语音的数据结构。
我们注意到等号右边的中间两项分别是一个矩阵和一个向量的表示形式,这便是因子分析的又一核心部分。这两个矩阵F和G包含了各自假想变量空间中的基本因子,这些因子可以看做是各自空间的特征向量。比如,F的每一列就相当于类间空间的特征向量,G的每一列相当于类内空间的特征向量。而两个向量可以看做是分别在各自空间的特征表示,比如hi就可以看做是Xij在说话人空间中的特征表示。在识别打分阶段,如果两条语音的hi特征相同的似然度越大,那么这两条语音就更确定地属于同一个说话人。
模型训练
容易理解,PLDA的模型参数一个有4个,分别是数据均值miu,空间特征矩阵F和G,噪声协方差sigma。模型的训练过程采用经典的EM算法迭代求解。为什么用EM呢?因为模型含有隐变量。
模型测试
在测试阶段,我们不再像LDA那样去基于consine距离来计算得分,而是去计算两条语音是否由说话人空间中的特征hi生成,或者由hi生成的似然程度,而不用去管类内空间的差异。在这里,我们使用对数似然比来计算得分。如下图所示:
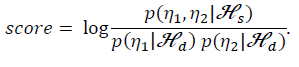
公式中,如果有两条测试语音,这两条语音来自同一空间的假设为Hs,来自不同的空间的假设为Hd,那么通过计算对数似然比,就能衡量两条语音的相似程度。得分越高,则两条语音属于同一说话人的可能性越大。
一个简化版本的PLDA
由于我们只关心区分不同的说话人的类间特征而不用去管同一个说话人的类内特征,所以其实没有必要向上面一样对类内空间G参数进行求解。于是,我们可以得到一个简化版本的PLDA,如下如:









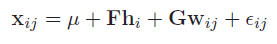















 733
733

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








