DNN库中matmul分析和设计

知识搬运工人

于 2024-08-23 16:07:23 发布

阅读量20

点赞数

文章标签：性能峰值计算

原文链接：https://zhuanlan.zhihu.com/p/564672391

版权

DNN库中matmul分析和设计 - 知乎 (zhihu.com)

前言

matmul函数是深度学习中最基本的函数，表示两个张量矩阵相乘，底层主要是通过GEMM和GEMV实现，GEMM即为矩阵乘矩阵，GEMV为矩阵乘向量。GEMM在深度学习中是十分重要的，全连接层以及卷积层基本上都是通过GEMM来实现的，而网络中大约90%的运算都是在这两层中。而一个良好的GEMM的实现可以充分利用系统的多级存储结构和程序执行的局部性来充分加速运算。

GEMM通用接口(BLIS\OPENBLAS\MKL)通常有如下参数：

cblas_sgemm(order, transA, transB, m, n, k, alpha, A, lda, B, ldb, beta, C, ldc)

参数	说明
order	存储方式：CblasColMajor或者CblasRowMajor
transA	矩阵A是否转置
transB	矩阵B是否转置
m	矩阵A、C维数
n	矩阵B、C维数
k	矩阵A、B维数
alpha	系数
A	A矩阵首地址
lda	A的leading dimention，即第一维度大小
B	B矩阵首地址
ldb	B的leading dimention，即第一维度大小
beta	系数
C	C矩阵首地址
ldc	C的leading dimention，即第一维度大小

简要说明下上面比较重要的参数：

order：包含CblasColMajor或CblasRowMajor，即为行主序和列主序。

列主序说明数据是按列一个个排序的，行主序说明数据是按行一个个排序的。

transA、transB：矩阵A、B是否转置。转置是一个数学名词，即照着右下45度做镜面反转。

可以看到列主序转置的内存排布和行主序非转置相同，行主序转置的内存排布和列主序非转置相同。

lda、ldb、ldc：这也是比较重要的参数，表示leading dimension，即第一维度的大小，在矩阵处理时，根据leading dimension，可以定位任意一个数据的位置。即addr(A[i, j])=A+i*lda+j.

需要说明一下，

1：深度学习中在调用matmul时，没有order和transA、transB等参数，是因为根据内存布局已经确定好了的，深度学习中数据默认情况下都是HW的布局，即先宽再高，和行主序非转置一致，所以深度学习默认的矩阵都是行主序非转置的情况。

2：GEMM当M或N为1时，就变成了GEMV，但是在这种情况下，GEMM性能非常差；所以，开发者一般在GEMM处理M或者N为1的情况下，会调用GEMV的代码。

矩阵乘法详细分析

GEMM根据维度、内存排布的不同，优化的方法也有所不同，常见的矩阵有大规模方阵，小矩阵、大规模窄阵等情况。但是万变不离其宗，学会分析，才能在多种多样的情形中找到最优解。

Blocked GEMM

简单的内存模型

假设计算机存储只有两个层级，快存储和慢存储，类比内存和缓存。
所有数据最初都在慢存储中。
- m ：在快存储和慢存储之间移动的内存元素(字)的数量.
- tm : 每次慢存储操作的时间
- f : 算术操作的数量
- tf : 每次算术操作的时间 << tm
- CI : f/m 每次慢存储访问的平均flops
当所有数据都在快存储中时，最短时间 f∗tf
实际时间 f∗tf+m∗tm=f∗tf∗(1+tm/tf∗1/CI)

当 CI 越大时，越接近 f∗tf ,代表性能越好。

GEMV例子：

{implements y = y + A*x}
for i = 1:n
    for j = 1:n
         y(i) = y(i) + A(i,j)*x(j)

分析GEMV

{read x(1:n) into fast memory}
{read y(1:n) into fast memory}
for i = 1:n
    {read row i of A into fast memory}
    for j = 1:n
         y(i) = y(i) + A(i,j)*x(j)
{write y(1:n) back to slow memory}

m=3n+n2
f=2n2
CI=f/m≈2

分析: m: A读取n*n次，x读取n次，y读取n次，y写入n次，共3n+n^2次。f:（乘法操作+加法操作）*n *n 次，共2n^2次。

GEMM例子：

{implements C = C + A*B}
for i = 1 to n
    for j = 1 to n
        for k = 1 to n
            C(i,j) = C(i,j) + A(i,k) * B(k,j)

{implements C = C + A*B}
for i = 1 to n
    {read row i of A into fast memory}
    for j = 1 to n
        {read C(i,j) into fast memory}
        {read column j of B into fast memory}
        for k = 1 to n
            C(i,j) = C(i,j) + A(i,k) * B(k,j)
{write C(i,j) back to slow memory}

m=n3+2n2
f=2n3=O(n3)
CI=f/m≈2

B需要读 n3 次，A需要读n2次，C需要读写共2n2次。

可见GEMV和GEMM的CI相同。

Blocked [Tiled] GEMM：

for i = 1 to N
    for j = 1 to N
        for k = 1 to N
            C(i,j) = C(i,j) + A(i,k) * B(k,j) {do a matrix multiply on blocks}

b=n/N

for i = 1 to N
    for j = 1 to N
        {read block C(i,j) into fast memory}
         for k = 1 to N
             {read block A(i,k) into fast memory}
             {read block B(k,j) into fast memory}
             C(i,j) = C(i,j) + A(i,k) * B(k,j) {do a matrix multiply on blocks}
{write block C(i,j) back to slow memory}

m=(2N+2)∗n2
f=2n3=O(n3)
CI=f/m≈n/N=b

C需要读写共2n2次, A需要读N∗n2次，B需要读 N∗n2 次。

可以看到Blocked后的GEMM，CI更大一些，性能要更好一些。

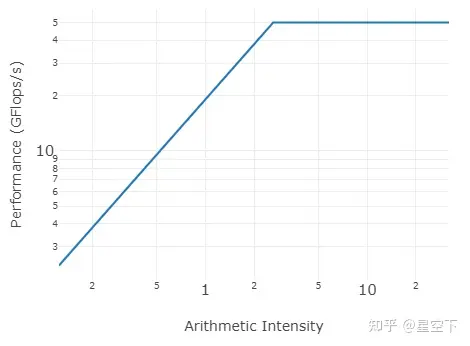
Roofline Performance Model

Roofline Model是一个性能模型，提出了使用 Arithmetic Intensity（计算强度）进行定量分析的方法，并给出了模型在计算平台上所能达到理论计算性能上限公式。

Roofline模型在此不再介绍，可以通过Michael Yuan：Roofline Model与深度学习模型的性能分析了解。

下面介绍下比较好用的benchmark的工具：GitHub - RRZE-HPC/likwid: Performance monitoring and benchmarking suite，通过该工具可以测试出机器的内存带宽。

先计算理论带宽：

# sudo dmidecode -t memory

Handle 0x0086, DMI type 17, 40 bytes
Memory Device
        Array Handle: 0x002E
        Error Information Handle: 0x0085
        Total Width: 128 bits
        Data Width: 64 bits
        Size: 32 GB
        Form Factor: DIMM
        Set: None
        Locator: CPU1_DIMMH0
        Bank Locator: P1 CHANNEL H
        Type: DDR4
        Type Detail: Synchronous Registered (Buffered)
        Speed: 2667 MT/s
        Manufacturer: Micron Technology
        Serial Number: 179AC90B
        Asset Tag: Not Specified
        Part Number: 36ASF4G72PZ-2G6D1   
        Rank: 2
        Configured Clock Speed: 2400 MT/s
        Minimum Voltage: 1.2 V
        Maximum Voltage: 1.2 V
        Configured Voltage: 1.2 V

理论带宽 = 2400 * 64 /8 = 19.2GBytes/s

DDR4 2666，频率是2400MT/s。对应下表可知为19.2Gbytes/s

# likwid-bench -t load_avx -W N:2GB:1
--------------------------------------------------------------------------------
Cycles:                 2060670560
CPU Clock:              1999976123
Cycle Clock:            1999976123
Time:                   1.030348e+00 sec
Iterations:             10
Iterations per thread:  10
Inner loop executions:  15625000
Size (Byte):            2000000000
Size per thread:        2000000000
Number of Flops:        0
MFlops/s:               0.00
Data volume (Byte):     20000000000
MByte/s:                19410.93
Cycles per update:      -nan
Cycles per cacheline:   0.000000
Loads per update:       1
Stores per update:      0
Load bytes per element: 8
Store bytes per elem.:  0
Instructions:           1093750016
UOPs:                   937500000
--------------------------------------------------------------------------------

通过benchmark测试出load的内存带宽是18.95GByte/s，和理论带宽基本一致。

通过CPUFP，可以计算出在Hygon 7285上单核FMA硬件最高峰值48GFlops.

所以对应的 AI=48/19.2=2.5 ，得到model 如下：

例子：

axpy:

void daxpy(size_t n, double a, const double *x, double *y) {
    size_t i;
    for (i = 0; i < n; i++) {
        y[i] = a * x[i] + y[i];
    }
}

flops = 2n

内存搬移 = 3n * 8 = 24n

AI=flops/sMemoryTraffic=flops/secondbytes/second=flopsbytes=2n/24n=1/12<2.5

则说明axpy属于内存带宽瓶颈区域。

AttainablePerformance(AI)=min{PeakPerformance,AI⋅PeakBandwidth}

推出axpy的最大性能是：

AttainablePerformance(1/12)=min{48,1/12⋅19.2}=1.6Gflops/s

gemv:

void dgemv(size_t n, const double* A, const double *x, double *y) {
    size_t i;
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            y(i) = y(i) + A(i,j)*x(j)
    }
}

flops = 2n2

内存搬移 = (3n+n2)∗8

AI=flops/sMemoryTraffic=flops/secondbytes/second=flopsbytes=112n+4

则说明dgemv属于内存带宽瓶颈区域。

假设n = 1024，AI = 0.25

AttainablePerformance(AI)=min{PeakPerformance,AI⋅PeakBandwidth}

推出gemm的最大性能是：

AttainablePerformance(4)=min{48,0.25∗19.2}=4.8Gflops/s

gemm:

void dgemm(size_t n, const double *A, const double *B, const double *C) {
    size_t i, j, k;
    double sum;
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            sum = 0.0;
            for (k = 0; k < n; k++) {
                sum = sum + A[i*n+k] * B[k*n+j];
            }
            C[i*n+j] = sum;
        }
    }
}

flops = 2n3

内存搬移 = 4n2∗8=32n2

AI=flops/sMemoryTraffic=flops/secondbytes/second=flopsbytes=n/16

则说明当n<40时属于内存带宽瓶颈区域，n>40属于计算瓶颈区域。

假设n = 64，AI = 4 > 2.5

AttainablePerformance(AI)=min{PeakPerformance,AI⋅PeakBandwidth}

推出gemm的最大性能是：

AttainablePerformance(4)=min{48,4⋅19.2}=48Gflops/s

总结

通过Roofline可以找出访存密集型算法和运算密集型算法，上述分析都是在最差的情况下。理想的处理器和缓存，即只有慢存储和快存储；冷启动，所有数据在DRAM中，且没有预取技术。

针对访存密集型的程序，可以通过soft perfetch，cache line等技术优化；预取可以减少内存搬移的次数，即减少AI中分母，增大AI，比如GEMV中A理想情况下（最差情况下）需要搬移 n2 次，在高速缓存和预取的情况下，可能只需要搬移n/2 * n/2次即可，则AI变大，GEMV性能提升。
针对计算密集型程序，可以通过SIMD等并行技术优化。

Register Blocked

以sgemm为例，数据类型为FP32, C=A∗B+C , A , B 和 C 维度分别为： m∗k , k∗n 和 m∗n 。假设所有的矩阵都是列主序(主要看C来确定循环顺序；如果是列主序，C也是列主序，那么先m后n，则是列主序的排序)。矩阵乘法的算法如下图：

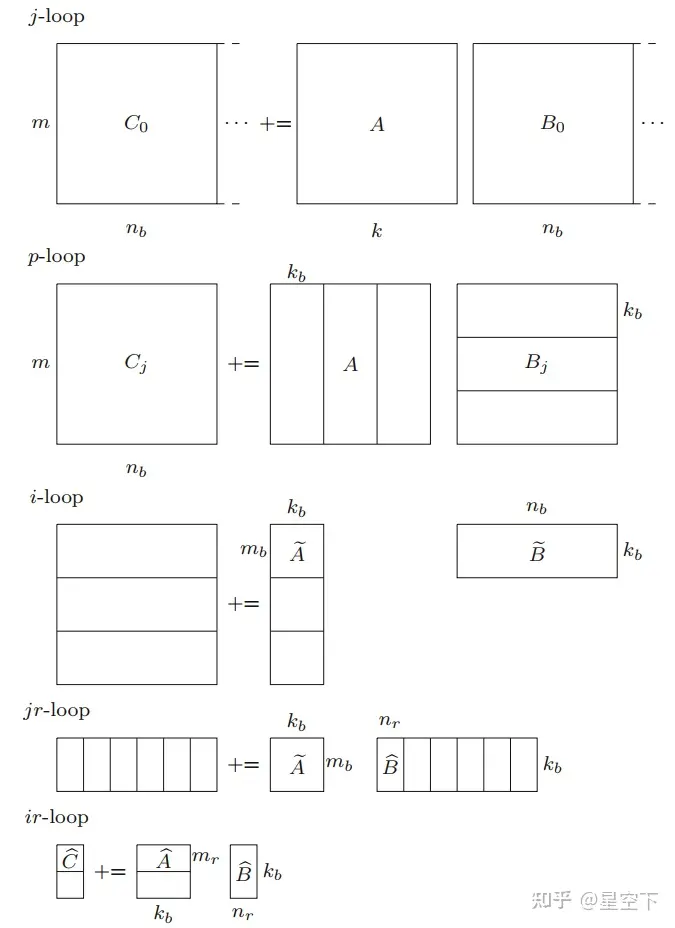
因为 mb 和nb应该分别是mr和nr的倍数，我们首先应该确定register blocking的size：mr和nr。X86中在inner kernel中使用SIMD指令，以开发目标机器的全部性能潜力。以XMM，FP32为例，有如下公式来充分利用寄存器。

（1）

若要sgemm inner kernel获取更高性能，则要充分利用向量寄存器，在上篇文章有说明，寄存器分块一般是：8x6(nr=8, mr=6)或者12x4(nr=12, mr=4)

（2）

Cache Blocking Size

GEMM若要取得高性能，需要使用分块矩阵，分块矩阵需要根据体系结构上的多级缓存来进行调整。将矩阵分成块可以对缓存重复利用，如果分块矩阵适合缓存的大小，它们可以留在缓存中，在计算过程中快速访问缓存并重用。

下面我们根据cache体系分析如何设定cache blocking size。

根据算法1，可以推测出复用参数如下：

Loop	Reused Data	Size of reused data	Reuse factor
6	Cr	mr x nr	kb
5	Br	kb x nr	mb / mr
4	Ab	mb x kb	nb / nr
3	Bb	kb x nb	m / mb
2	Conlumn panel of C	m x nb	k / kb
1	Matrix A	m x k	n / nb

识别重要的数据片段很重要，因为它告诉我们应该将哪些数据部分保存在缓存中，以便实现快速访问并减少缓存浪费。上表表面，随着循环深度的增加，重用数据的size会变小，这很好的匹配了内存层次结构，其中较快的内存层比较慢的内存层具有更小的容量。

确定最小的mr, nr，它们足够大，以摊销两个相互依赖的FMA指令之间的延迟。
找出最大的kb，确保精确的存放到L1cache中的 A^ 。它是由A^(表示 CA^ )所占据的结合度决定的。

（3）

和

（4）

说明： NLi 是Li cache sets的数量，CLi是Li cache中Cache line的size。 SDATA 是每个元素的size。 WLi 是Li cache的结合度(way的概念)；最小mr，nr才能保证数据加载量最少。

找出最大的mb，确保精确的存放到L2 cache中的 B^ 。它是由A~(表示 DA~ )所占据的结合度决定的。

（5）

和

（6）

（7）

以Hygon Dhyana系列CPU为例：L1 cache 是32KB。 A^ 和 B^ 应该填充L1 cache，并保留B^。

(8)

说明：根据 mr+nr∈[12,16] , 可以获取 kb<680 .

A~ 、 B^ 和C^应该填充L2 cache：

(9)

对于L3 cache，尽量让B~ 保存到L3 cache中，实际操作中，B~占L3 cache一半左右，这样 A~ 、C^中的数据就不会驱逐的B~ 中的元素。

（10）

根据上述公式，从理论上分析出：，，，，mr，nr，mb，nb，kb 等分块的取值范围。然后根据实际测试，找出最适合的取值，下面举个例子如下，举例子前首先获取cache line的大小。

如何查看机器cache信息

li cache相关信息：

sets:
cat /sys/devices/system/cpu/cpu0/cache/index0/number_of_sets

ways:
cat /sys/devices/system/cpu/cpu0/cache/index0/ways_of_associativity

cache line
cat /sys/devices/system/cpu/cpu0/cache/index0/coherency_line_size

cache size
cat /sys/devices/system/cpu/cpu0/cache/index0/size

默认情况下，index0为L1data，index1为L1instruction，index2为L2 cache，index3为L3 cache。

若使用XMM，数据类型是FP32，即 SDATA=4

通过公式1和2，可以算出mr = 4，nr = 12。

通过公式4，可以算出 CA^=1 ，通过公式3，可以算出kb = 256，此时kb满足公式8.

根据公式7，可以算出 DB^=1 ，通过公式5和6，算出mb = 384,此时mb满足公式9.

根据公式10，可以算出nb <= 4096.

说明：上面是通过公式得到的理论值，实际使用时，通过tuning找到最适合的block size。

(持续更新中。。。)

知识搬运工人

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
DNN库中matmul分析和设计

matmul函数是深度学习中最基本的函数，表示两个张量矩阵相乘，底层主要是通过GEMM和GEMV实现，GEMM即为矩阵乘矩阵，GEMV为矩阵乘向量。GEMM在深度学习中是十分重要的，全连接层以及卷积层基本上都是通过GEMM来实现的，而网络中大约90%的运算都是在这两层中。而一个良好的GEMM的实现可以充分利用系统的多级存储结构和程序执行的局部性来充分加速运算。参数说明order存储方式：CblasColMajor或者CblasRowMajortransA矩阵A是否转置transB。
复制链接

扫一扫