CSS3变形介绍
2012年9月,W3C组织发布了CSS3变形工作草案。CSS3变形是一些效果的集合,比如平移、旋转、缩放和倾斜效果,每个效果都被称作为变形函数(Transform Function),它们可以操控元素发生旋转、缩放、和平移等变化,还可以结合CSS3的transition和动画的keyframe产生复杂的动画效果。这些效果在之前都需要依赖图片、Flash或JavaScript才能完成。而现在使用纯CSS来完成这些变形则无需加载这些额外的文件,再一次提升了开发效率,还提高了页面的执行效率。CSS3变形允许CSS把元素转变为2D 或3D空间,这个草案包括了CSS3 2D变形和CSS3 3D变形。
transform属性
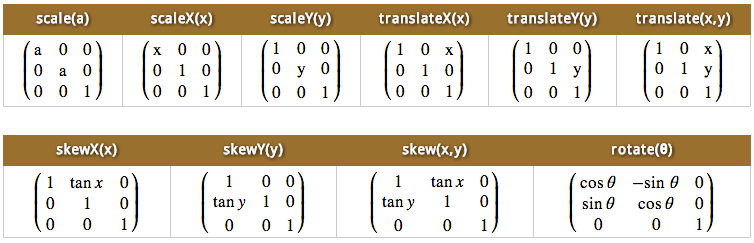
CSS3的变形(transform)属性让元素在一个坐标系统中变形。transform属性的基本语法如下:
transform:none | <transform-function> [<transform-function>]*transform属性可用于内联元素和块元素。其默认值为none,表示不进行变形。transform另一个属性值是一系列的。表示一个或多个变形函数,以空格分开;即我们同时对一个元素进行变形的多种属性操作,例如rotate、scale、translate等。但这里需要提醒一下,以往我们叠加效果都是用逗号(“,”)隔开,但在transform中使用多个transform-function时却需要用空格隔开。
2D transform常用的transform-function的功能:
- translate():用来移动元素,可以根据X轴和Y轴坐标重新定位元素位置。在此基础上有两个扩展函数:translateX()和translateY()。
- scale():用来缩小或放大元素,可以使用元素尺寸发生变化。在此基础上有两个扩展函数:scaleX()和scaleY()。
- rotate():用来旋转元素。
- skew():用来让元素倾斜。在此基础上有两个扩展函数:skewX()和skewY()。
- matrix():定义矩阵变形,基于X轴和Y轴坐标重新定位元素位置。
3D transform常用的transform-function的功能:
- translate3d():移动元素,用来指定一个3D变形移动位移量。
- translatez():指定3D位移在Z轴的位移量。
- scale3d():用来缩放一个元素。
- scaleZ():指定Z轴的缩放向量。
- rotate3d():指定元素具有一个三维旋转的角度。
- rotateX()、rotateY()和rotateZ():让元素具有一个旋转角度。
- perspective():指定一个透视投影矩阵。
- matrix3d():定义矩阵变形。
一些重要属性:
- transform-origin属性指定元素的中心点在哪。后面增加了第三个数transform-origin-z,控制元素三维空间中心点。
- perspective属性相对于观众产生一个3D场景,看3D物体,眼睛到画布的距离。 它需要应用到变形元素的祖先元素上。
- perspective-origin为视点的位置。
- backface-visibilty属性用来设置背面的可见性。
- 设置transform-style的值为preserve-3d时,建立一个3D渲染环境。
本篇介绍2D变形。
在CSS3 2D变形中主要包含的一些基本功能如下:
位移translate()函数
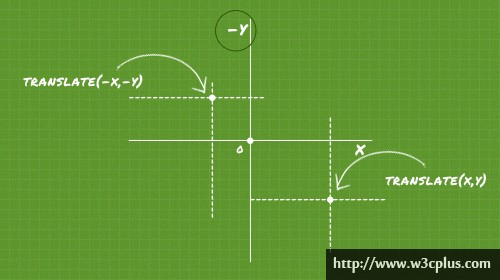
使用translate()函数,可以把元素从原来的位置移动到指定位置,而不影响在X、Y轴上任何组件。
translate()函数的使用语法如下:
translate(tx) 或者 translate(tx,ty)translate()函数可以取一个值tx,也可以同时取两个值tx和ty,其取值具体说明如下:
- tx是一个代表X轴(横坐标)移动的向量长度,当其值为正值时,元素向X轴右方向移动,反之其值为负值时,元素向X轴左方向移动。
- ty是一个代表Y轴(纵向标)移动的向量长度,当其值为正值时,元素向Y轴下方向移动,反之其值为负值时,元素向Y轴上方向移动。如果ty没有显式设置时,相当于ty=0。
结合起来,translate()函数移动元素主要有以下三种移动:
- 水平移动:向右移动translate(tx,0)和向左移动translate(-tx,0);
- 垂直移动:向上移动translate(0,-ty)和向下移动translate(0,ty);
- 对角移动:右下角移动translate(tx,ty)、右上角移动translate(tx,-ty)、左上角移动translate(-tx,-ty)和左下角移动translate(-tx,ty)。
如果我们要将对象沿着一个方向移动,比如说沿着水平轴或者纵轴移动,可以使用translate(tx,0)和translate(0,ty)来实现。其实在变形中还为单独一个方向移动对象提供了更简单的方法:
translateX():水平方向移动一个对象。通过给定一个X轴方向的数值指定对象沿水平轴方向的位移。简单点说,对像只向X轴进行移动,如果值为正值,对像向右移动;如果值为负值,对像向左移动。
translateY():纵轴方向移动一个对象。通过给定一个Y轴方向的数值指定对象沿纵轴方向的位移。简单点说,对象只向Y轴进行移动,如果值为正值,对象向下移动;如果值为负值,对像向上移动。
这两个函数和前面介绍的translate()函数不同的是每个方法只接受一个值。所以:transform:translate(-100px,0)
实际上等于transform:translateX(-100px);
transform:translate(0,-100px)
实际上等于transform:translateY(-100px)。
缩放scale()函数
缩放scale()函数让元素根据中心原点对对象进行缩放。默认值为1。因此0.01到0.99之间的任何值,使一个元素缩小;而任何大于或等于1.01的值,将元素放大。
语法如下:
scale(sx) 或 scale(sx,sy)它可以接受一个值,也可以同时接受两个值,如果只有一个值时,其第二个值默认与第一个值相等。例如,scale(1,1)元素不会有任何变化,而scale(2,2)让元素沿X轴和Y轴放大两倍。其取值简单说明如下:
- sx:用来指定横向坐标(X轴)方向的缩放向量,如果值为0.01~0.99之间,会让对象在X轴方向缩小,如果值大于或等于1.01,对象在X轴方向放大。
sy:用来指定纵向坐标(Y轴)方向的缩放量,如果值为0.01~0.99之间,会让对象在Y轴方向缩小,如果值大于或等于1.01,对象在Y轴方向放大。
scale()函数和translate()函数极其相似,除了能通过scale()函数使用元素水平方向和垂直方向同时缩放(也就是元素沿X轴和Y轴同时缩放)之外,也可以使元素仅沿着X轴或Y轴方向缩放:
scaleX():相当于scale(sx,1)。表示元素只在X轴(水平方向)缩放元素,其默认值是1。
scaleY():相当于scale(1,sy)。表示元素只在Y轴(纵横方向)缩放元素,其默认值是1。
注:
- 在scale()函数中,取值除了可以取正值之外,同时还可以取负值。只不过取负值时,会先让元素进行翻转,然后在进行缩放。
- scale()函数对元素进行缩放时,都是以元素的中心为基点,但可以通过transform-origin来改变元素的基点。
旋转rotate()函数
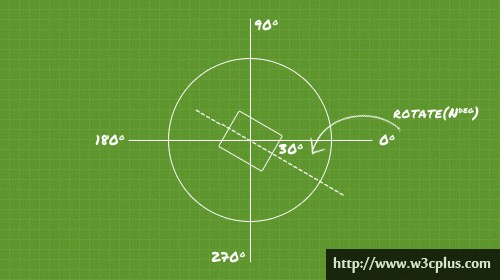
旋转rotate()函数通过指定的角度参数对元素根据对象原点指定一个2D旋转。它接受一个角度值,用来指定旋转的幅度。如果这个值为正值,元素相对原点中心顺时针旋转;如果这个值为负值,元素相对原点中心逆时针旋转。
使用语法如下:
rotate(a);rotate()函数只接受一个值,其属性值简单说明如下:
a:代表的是一个旋转的角度值。其取值可以是正的,也可以是负的。如果取值为正值时,元素默认之下相对元素中心点顺时针旋转;如果取值为负值时,元素默认之下相对元素中心点逆时针旋转。
注:
- 在默认之下,rotate()函数旋转元素是相对于元素中心点进行旋转,同样,我们可以通过transform-origin属性重置元素的旋转原点。
倾斜skew()函数
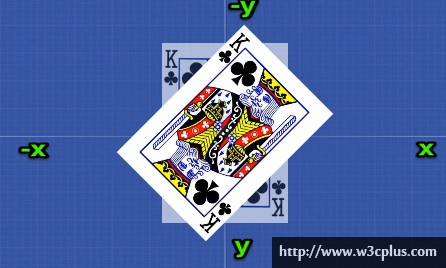
倾斜skew()函数能够让元素倾斜显示。它可以将一个对象以其中心位置围绕着X轴和Y轴按照一定的角度倾斜。这与rotate()函数的旋转不同,rotate()函数只是旋转,而不会改变元素的形状。skew()函数不会旋转,而只会改变元素的形状。
语法格式如下:
skew(ax) 或者 skew(ax,ay)其属性值说明如下:
- ax:用来指定元素水平方向(X轴方向)倾斜的角度。
- ay:用来指定元素垂直方向(Y轴方向)倾斜的角度。如果未显式的设置这个值,其默认为0。
看这是旋转:
这是倾斜:
倾斜skew()函数和CSS3中变形中的translate()、scale()函数一样,除了可以使用skew(tx,ty)函数让元素相于元素中心为原点在X轴和Y轴倾斜之外,还可以使用skewX()和skewY()函数让元素只在水平或垂直方向倾斜。
- skewX():相当于skew(ax,0)和skew(ax)。按给定的角度沿X轴指定一个倾斜变形。skewX()使元素以其中心为基点,并在水平方向(X轴)进行倾斜变形。
- skewY():相当于skew(0,ay)。按给定的角度沿Y轴指定一个倾斜变形。skewY()用来设置元素以其中心为基点并给定的角度在垂直方向(Y轴)倾斜变形。
在默认情况之下,skew()函数都是以元素的原中心点对元素进行倾斜变形,但是我们同样可以根据transform-origin属性,重新设置元素基点对元素进行倾斜变形。另外,skew()函数和制图软件中的变形工具所起作用类似。
矩阵matrix()函数
Web设计师可以使用rotate()、skew()、scale()和translate()函数来满足他们的变形需要,那我们为什么要劳烦矩阵matrix()呢?为了实现复杂的
2D变形。在CSS3中的变形函数都可以使用matrix()函数来代替,例如:
#object {
transform-origin: 0 0;
transform: rotate(15deg) translateX(230px) scale(1.5, 2.6) skew(220deg, -150deg) translateX(230px)
}使用一个矩阵matrix()规则变成如下:
#object {
transform-origin: 0 0;
transform: matrix(1.06, 1.84, 0.54, 2.8, 466px, 482px)
}要整明白CSS3变形中的matrix()函数,我们先要了解矩阵matrix是怎么一回事。
在CSS3中变形的matrix分为两种,一种是2D矩阵,另外一种是3D矩阵。先从简单的入手——2D矩阵matrix。CSS3中的2D矩阵matrix总共提供了六个参数:a,b,c,d,e和f,其基本写法如下:
matrix(a,b,c,d,e,f)这六个参数,对应的矩阵就是:
在开始之前,先来复习一下3 x 3矩阵的乘积:
弄明白3x3的矩阵之后,即可知道matrix计算方法。x和y是元素初始原点的坐标,x’和y’则是通过矩阵变换后得到的新原点坐标。通过中间的那个3x3的变换矩阵,对原先的坐标施加变换,就能得到新的坐标了。依据矩阵变换规则即可得到:x’=ax+cy+e和y’=bx+dy+f:
为了更好的理解,我们一起来看一个简单的例子。假设矩阵参数如下:
transform: matrix(1,0,0,1,50,50);/*a=1,b=0,c=0,d=1,e=50,f=50*/矩阵偏移元素的中心点,假设是(0,0),即x=0,y=0。
也就是计算得出x’=50,y’=50。即元素的原点由(0,0)移动到(50,50)的位置。实际上transform:matrix(1,0,0,1,50,50);就等同于transform: translate(50px,50px)。
接下来分别看看CSS3变形中matrix()和各变形函数之间的关系:
translate()转换成matrix()
transform:translate(tx,ty)
matrix(1,0,0,1,tx,ty)/*tx,ty分别对应X和Y轴的增量*/其对应的矩阵图:
scale()转换成matrix()
transform:scale(sx,sy)
matrix(sx*x,0,0,sy*y,0,0);/*sx和sy分别对应X轴和Y轴的缩放比率*/其对应的矩阵图:
rotate()转换成matrix()
transform:rotate(a)
matrix(cos(a),sin(a),-sin(a),cos(a),0,0);/*cos(a)和sin(a)是指旋转度转*/它对应的矩阵是:
skew()转换成matrix()
transform:skew(ax,ay)
matrix(1,tan(ay),tan(ax),1,0,0)/*tan(ax)和tan(ay)是对应的倾斜角度*/其对应的矩阵图:
下图就是所有CSS3变换与矩阵等价的关系图:
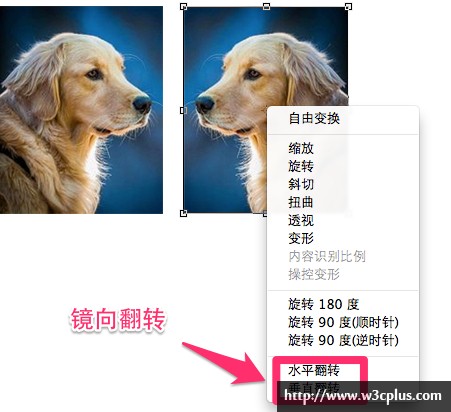
matrix()实现镜像
在制图软件中变形工具除了旋转、倾斜、位移、缩放等还有镜向(水平镜向、垂直镜向):
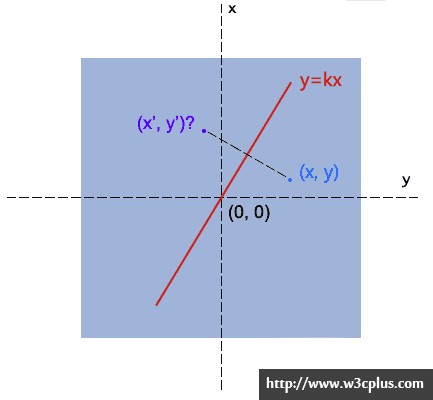
但镜像对称在CSS3变形中没有相应的简化操作。只能通过矩阵matrix()来实现。通过前面的内容介绍,我们清楚的知道,元素变形的原点是其中心点(在没有显式的重置之外),那么这个镜向的原点也不例外。因为对称轴永远经过原点,因此,任意对称轴都可以用y=k*x直线表示。则matrix表示就是:
matrix((1-k^2)/(1+k^2),2k / (1 + k^2),2k/(1+k^2),(k^2-1)/(1+k^2),0,0)
这个如何得到的呢?我们来看看实现的过程。如下图所示,已经y=k*x,并且知道点(x,y),求其对称点(x’,y’)的坐标位置:
很简单,一是垂直,二是中心点在轴线上,因此有:
(y-y') / (x - x') = -1/ k → ky-ky' = -x+x'
(x + x') / 2 * k = y + y' → kx+kx' = y+y'把x’和y’提出来,就有:
x' = (1-k^2)/(k^2+1) *x + 2k/(k^2+1) *y;
y' = 2k/(k^2+1) *x + (k^2-1)/(k^2+1) *y;再结合矩阵公式:
x' = ax+cy+e;
y' = bx+dy+f;就可以得到:
a = (1-k^2)/(k^2+1);
b = 2k/(k^2+1);
c = 2k/(k^2+1);
d = (k^2-1)/(k^2+1);也就是上面matrix矩阵中的参数值。
CSS3 2D Ttransform兼容性
CSS3的2D变换虽然得到众多主流浏览器的支持,但在实际使用的时候需要添加浏览器各自的私有属性:
IE9中使用2D变形时,需要添加-ms-私有属性,在IE10+版本开始支持标准版本。
Firefox3.5至Firefox15.0版本需要添加-moz-的私有属性,在Firefox16+版本开始支持标准版本。
Chrome4.0+开始支持2D变形,在实际使用的时候需要添加-webkit-私有属性。
Safari3.1+开始支持2D变形,在实际使用的时候需要添加-webkit-私有属性。
Opera10.5+开始支持2D变形,在实际使用的时候需要添加-o-私有属性,但在Opera12.1版本不需要添加私有属性,不过在Opera15.0+版本需要添加私有属性-webkit-私有属性。
移动设备iOS Safari3.2+、Android Browser2.1+、Blackberry Browser7.0+、Opera
Mobile14.0+、Chrome for Android25.0+需要添加私有属性-webkit-,而Opera
Mobile11.0至Opera Mobile12.1和Firefox for Android19.0+不需要使用浏览器私有属性。








 本文详细介绍了CSS3中的2D变形,包括transform属性、translate()、scale()、rotate()、skew()和matrix()函数,以及它们的用法和兼容性。CSS3 2D变形提供了一种无需依赖图片、Flash或JavaScript即可实现元素旋转、缩放、平移和倾斜的方法,提升开发效率和页面性能。
本文详细介绍了CSS3中的2D变形,包括transform属性、translate()、scale()、rotate()、skew()和matrix()函数,以及它们的用法和兼容性。CSS3 2D变形提供了一种无需依赖图片、Flash或JavaScript即可实现元素旋转、缩放、平移和倾斜的方法,提升开发效率和页面性能。



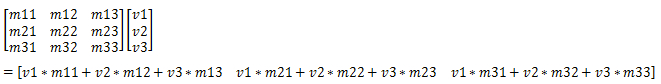
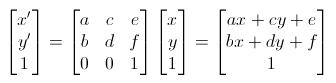
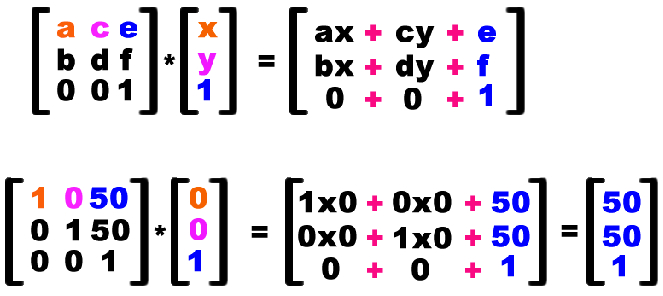
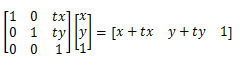
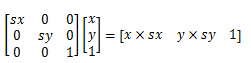
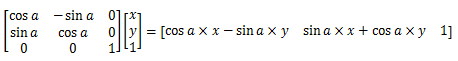
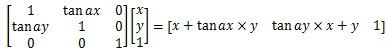
















 4459
4459

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








