作为一个没接触过机器学习或者深度学习(或者叫做人工智能AI,其实严格意义上只是人工智能的一个分支)的小白(没错就是我),参加了公司组织的两次培训,自己终于对这个领域有一个感性的认识了,谢谢我东家!!爱你,么么哒!!
机器学习

线性回归(linear regression)
英文好的建议直接阅读(人家写的真心的好啊): https://towardsdatascience.com/introduction-to-machine-learning-algorithms-linear-regression-14c4e325882a 特别提醒: 原文以及我上传到CSDN上的数据集的y_train的第214个元素为NAN,所以直接使用原文中的代码就会出错……,需要自己先处理一下数据。
线性回归由两个单词组成 线性 和回归(废话啊!!兄弟,请你原谅我低下的智商,我以前确实不怎么理解的,一直把 线性回归作为一个专用名词使用的!) 。首先回归 是根据自变量(输入)来找到一个与因变量(输出)的对应关系,如果这个对应关系足够好,那么就可以将这个对应关系(model)用来预测,或者用来解释输入和输出之间的关系。

上图是典型的线性回归, 红线是利用某种方法(这种简单的模型,一般都用最小二乘法(可以参考一位同学的介绍,虽然我看不懂:如何理解最小二乘法? ))得出的最佳回归直线, 可用下面的方程描述:
y
=
a
0
+
a
1
x
线性方程
y=a_0+a_1x \qquad\text{线性方程}
y=a0+a1x线性方程
那么对于此类线性回归问题,就是寻找最佳的
a
0
a_0
a0 和最佳的
a
1
a_1
a1 ,其中
a
0
a_0
a0叫做截距(是不是很熟悉,少年),
a
1
a_1
a1叫做斜率。对于这个线性回归问题,有以下两个牛逼的概念:
Cost Function(损失函数,误差函数)
如果你在平时工作中叫此类函数叫做损失函数,那么你年薪有可能是50,如果你叫做误差函数,那么就显得逼格不够高,那有可能智能得到20了……,损失函数如下:
J
m
i
n
=
1
n
∑
i
=
0
n
(
p
r
e
d
i
−
y
i
)
2
J_{min}=\frac{1}{n}\sum_{i=0}^{n}(pred_i-y_i)^2
Jmin=n1i=0∑n(predi−yi)2
我们的目标是最小化目标函数,这时你也许发现这个函数还叫做(均方差(Mean Squared Error(MSE)),不要使用这个名字,不要使用这个名字,不要使用这个名字!!这样你的年薪也许会降5),
Gradient Descent(梯度下降)
如果你上过小学一年级,你就会知道对于一个一元二次方程求导数,可以得到一个一元一次方程,然后就能根据倒数的性质(驻点)得到一元二次方程的最小值或最大值所在的位置。总的来说,梯度下降就是这类问题,不过是通过求偏导(这应该是小学二年的内容)。对于凸函数(像一元二次方程那样的),其全局最小解就是局部最小解!不过对于非凸函数,这个最小化问题就麻烦些,因为局部最小解不一定为全局最小解(当然我们可以通过增加额外迭代步数来做,但是依旧不能保证局部最小解就是全局最小解!!)。
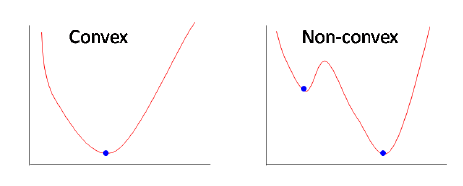
另一种方法是加大迭代步长,防止最优化问题陷入局部最优解。但是也有可能出现震荡问题,造成越过全局最小解。这里的迭代的大小,在深度学习里面就叫做:学习率(同学,一定要用这个!这样才能有高工资!)。

以下是咱们都不想看的公式推导:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{aligned…
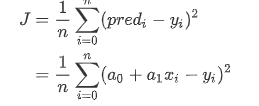
注意我要变形了:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{aligned…
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{aligned…

所以迭代方法为:
a
0
=
a
0
−
α
2
n
∑
i
=
0
n
(
p
r
e
d
i
−
y
i
)
a_0=a_0-\alpha\frac{2}{n}\sum_{i=0}^{n}(pred_i-y_i)
a0=a0−αn2i=0∑n(predi−yi)
a 1 = a 1 − α 2 n ∑ i = 0 n ( p r e d i − y i ) x i a_1=a_1-\alpha\frac{2}{n}\sum_{i=0}^{n}(pred_i-y_i)x_i a1=a1−αn2i=0∑n(predi−yi)xi
这里你也许会问,为什么呢?对于一元函数的极值问题,我们好理解。
对于多元函数的偏导数的几何意义:

所以对于 a 0 a_0 a0 的迭代步长是: 以上一个 a 0 a_0 a0 点做平行于 a 0 J a_0J a0J平面的切线,此切线与 a 0 a_0 a0轴的交点为原始步长, 最终步长为 α 2 n ∑ i = 0 n ( p r e d i − y i ) \alpha\frac{2}{n}\sum_{i=0}^{n}(pred_i-y_i) αn2∑i=0n(predi−yi) . 在这里 α \alpha α为学习率。
数据集
做实验的数据集的链接: https://www.kaggle.com/andonians/random-linear-regression/data
我也在CSDN上上传了一份: https://download.csdn.net/download/xuanyuanlei1020/12040336
将训练数据集和验证数据集的Data Set 的分布如下:

代码实现
这里数据集的
y
t
r
a
i
n
y_{train}
ytrain有一个nan 值,我的处理方法是将上一组数据替代了那个数据。
import pandas as pd
import numpy as np
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')
x_train = df_train['x']
y_train = df_train['y']
x_test = df_test['x']
y_test = df_test['y']
x_train = np.array(x_train)
y_train = np.array(y_train)
x_test = np.array(x_test)
y_test = np.array(y_test)
x_train = x_train.reshape(-1,1)
x_test = x_test.reshape(-1,1)
y_train = y_train.reshape(-1,1)
y_test = y_test.reshape(-1,1)
## Linear Regression
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score
n = 700
alpha = 0.0001
a_0 = np.zeros((n,1))
a_1 = np.zeros((n,1))
epochs = 0
while(epochs < 1000):
y = a_0 + a_1 * x_train
error = y - y_train
mean_sq_er = np.sum(error**2)
mean_sq_er = mean_sq_er/n
a_0 = a_0 - alpha * 2 * np.sum(error)/n
a_1 = a_1 - alpha * 2 * np.sum(error * x_train)/n
epochs += 1
if(epochs%10 == 0):
print(mean_sq_er)
y_prediction = a_0[0] + a_1[0] * x_test
print('R2 Score:',r2_score(y_test,y_prediction))
y_plot = []
for i in range(100):
y_plot.append(a_0[0] + a_1[0] * i)
plt.figure(figsize=(5,5))
plt.scatter(x_test,y_test,color='red',label='GT')
plt.plot(range(len(y_plot)),y_plot,color='black',label = 'pred')
plt.legend()
plt.show()
最终结果:

迭代次数造成的不同(红字为迭代次数,总的趋势是迭代越多,效果越好,但是收益越来越低):

使用sklearn 库
import pandas as pd
import numpy as np
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')
x_train = df_train['x']
y_train = df_train['y']
x_test = df_test['x']
y_test = df_test['y']
x_train = np.array(x_train)
y_train = np.array(y_train)
x_test = np.array(x_test)
y_test = np.array(y_test)
x_train = x_train.reshape(-1,1)
x_test = x_test.reshape(-1,1)
y_train = y_train.reshape(-1,1)
y_test = y_test.reshape(-1,1)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
clf = LinearRegression(normalize=True)
clf.fit(x_train,y_train)
y_pred = clf.predict(x_test)
print(r2_score(y_test,y_pred))
结果: r2_score: 0.9888016427276151
可以发现,封装好的函数是又快有好……,但是咱们也要理解为什么。
损失函数的图像:

看到这个图像是不是觉得其值和 A_0没啥关系,截取局部得到的结果如下:

这张图就说明了 A 0 A_0 A0也是影响损失函数的,就是在驻点附近变化较小,让人误以为没有影响。
或者改变取值范围也能直观的观察出来:
a_0_list = np.linspace(-2,2,2000)
a_1_list = np.linspace(0.9,1,2000)

代码实现:
import pandas as pd
import numpy as np
df_train = pd.read_csv('train.csv')
df_test = pd.read_csv('test.csv')
x_train = df_train['x']
y_train = df_train['y']
x_test = df_test['x']
y_test = df_test['y']
x_train = np.array(x_train)
y_train = np.array(y_train)
x_test = np.array(x_test)
y_test = np.array(y_test)
x_train = x_train.reshape(-1,1)
x_test = x_test.reshape(-1,1)
y_train = y_train.reshape(-1,1)
y_test = y_test.reshape(-1,1)
# we all know a_0 在 0.00895864 附近
# a_1 在 0.99892006 附近
a_0_list = np.linspace(-0.15,0.05,2000)
a_1_list = np.linspace(-0.0,2,2000)
A0, A1 = np.meshgrid(a_0_list,a_1_list)
def J_function(a_0,a_1):
y = a_0 + a_1 * x_train
error = y - y_train
mean_sq_er = np.sum(error**2)
mean_sq_er = mean_sq_er/700
return mean_sq_er
J_value = A0.copy()
for i in range(2000):
if(i>900 and i<1100):
print('============================================')
for j in range(2000):
J_value[i][j] = J_function(A0[i][j],A1[i][j])
if(i> 900 and i<1100):
if(i != 998 and j%200 == 0 ):
print('i: '+ str(i) + ' j: '+ str(j) + " A0: "+ str(A0[i][j]) + ' A1: ' + str(A1[i][j]) + ' J_value: ' + str(J_value[i][j]))
elif(i == 998):
print('i: ' + str(i) + ' j: ' + str(j) + " A0: " + str(A0[i][j]) + ' A1: ' + str(
A1[i][j]) + ' J_value: ' + str(J_value[i][j]))
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection='3d')
#ax.contour3D(A0,A1,J_value, 50, cmap = 'binary')
#ax.sccatter3D(A0,A1,J_value)
ax.plot_surface(A0,A1,J_value)
ax.set_xlabel('a_0')
ax.set_ylabel('a_1')
ax.set_zlabel('J_value')
plt.show()
fig2 = plt.figure(2)
plt.plot(A0[998],J_value[998])
plt.show()
后话: 就是这么一个简单线性回归就花费了我很大的精力,不知道以后会不会能够全盘理解机器学习和深度学习。加油吧!
什么是R2 Score? 从零开始学机器学习12 MSE、RMSE、R2_score





















 1167
1167











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








