模2运算_模二除法和CRC循环冗余校验@n个奇数相加结果的奇偶性的讨论

模二运算:

• CRC码是基于模2运算而建立编码规律的校验码🎈

模2加/模2减

• 模二加和模二减可以视为亦或(xor)运算
• 模2运算的特点是
  • 不考虑进位和借位的运算
• 其规律如下：
  • 模2加和模2减的结果是相等的，x modadd 2=x modsub 2
  • 即0±1=1,0±0=0,1±0=1,1±1=0
• 总结,二进制数(0,1)的模2加和模2减结果上都等同于异或运算
  • 可见，两个相同数的模2和恒为0.

模2乘/除

• 模2乘是按模2和求部分积之和

• 模2除是按模2减求部分余数

• 解释:

  • 模2乘除法的计算方法和笔算乘法类似步骤类似

    • 但是

      • 乘法时的使用的若干次普通加法被改成了模2加
      • 除法时的使用的若干次普通减法被改成了模2减
      • 又因为模二加和模二减效果一样,所以它们都可以通过按位异或得到本位运算结果

模2除

• 上商的原则是：

  • 当部分余数的首位为1时，上商1；
  • 当部分余数的首位为0时，上商0;
  • 这是因为,被除数的最高位总是非0的,对于二进制而言,总是1
    • 就好像我们做十进制除法,被除数不会写0开头的(总是处理成非0开头的(1~9))
    • 除数也是一样的情况(对于二进制,也总是1开头)
    • 所以对于二进制,除数和被除数都是形如$s=1\cdots x_0,d=1\cdots d_0$:

• 每求一位商应使部分余数减少一位🎈

  • 指部分和的高位(用过就不再用了)

    • 且,根据上面的分析,上商后,部分余数最高位和除数乘以本位商最高位是一致的

  • 低位部分是要继续用的

  • 当部分余数的位数小于除数的位数时，该余数即为最后余数。

• 对于除法,注意由于没有进位和借位,🎈

  • 除数的位数m小等于被除数或部分余数的位数n,那么依然继续上商

部分积之和的比较

• 类似于我们列竖式计算的中间计算过程的各行中间结果
• 部分积的算术和:
  • 就是各个中间结果的直接加和
• 部分积的模二和:
  • 以模二和的加法规则(也就是按位异或)来求和中间结果

异或运算的相关规律🎈

任意数量的0相异或结果为0

• 由$0\oplus 0=0$
  • n个0相异或会被化简为$n-1$个0相异或
  • 递推下去,只剩下一个0
  • $0\oplus 0\oplus \cdots \oplus 0=0$

n个1相异或

• $1\oplus 1=0$

• $0\oplus 1=1\oplus 0=1$

• $A\oplus 1=\overline{A}$

• $A\oplus 0=A$

• n个1连续亦或中得递推公式$y_{n+1}=y_n\oplus 1=\overline{y_n}$

  • 从这个地推公式中可以看出,每追加一个和1亦或的运算,结果将之前的结果取反

• n	$y=\underset{i=1}{\stackrel{n}{\oplus }}1$
  2	0
  3	1
  4	0
  5	1
  …	…
  2i	0
  2i+1	1
  …	…

• 可以得出以下结论:

  • 偶数个1 相亦或 ,结果为0

  • 奇数个1 相亦或,结果为1

• 事实上,在二进制范畴内:(用枚举真值表的方式可以轻松证明)

  • 和1异或相当于取反
    • $b\oplus 1=1\oplus b=\overline{b}$
  • 和0异或相当于保持:
    • $b\oplus 0=0\oplus b=b$
    • 由于和零亦或会保持亦或前的结果这种特性,对于任意一个二进制串的异或结果和去掉所有的0后再相异或的结果是一致的
    • 例如:
      • $1\oplus 0\oplus 1\oplus 1\oplus 0=1\oplus 1\oplus 1=1$

交换律

• 经过上述分析可知,异或运算满足交换律

结合律

• 根据上面的分析,可以知道,异或运算满足结合律

  • 包含零的一系列数的亦或运算结果等于去除所有0后的亦或结果
  • 因而任意一个连续亦或的表达式,只需要关注其中的1的数量即可(奇偶性)

• $$\begin{gathered} y_1=a_1\oplus a_2\oplus \cdots \oplus a_n \\ {y}_2=P_1\oplus P_2\oplus \cdots \oplus P_t \\ =T_1\oplus T_2\oplus \cdots \oplus T_s \end{gathered}$$

  • $P_i,i=1,2,\cdots ,t$要么含有奇数个1,要么含有偶数个1,将含有偶数个1的$P_i$去掉(不影响结果)
  • 得到$T_i=1,i=1,\cdots ,s$,各含有奇数个1
  • 如果$a_1\cdots ,a_n$含有奇数个1,则由奇数-偶数=奇数,偶数个奇数相加结果为偶数可知s只有可能为奇数,
  • 如果$a_1\cdots ,a_n$含有偶数个1,则由偶数-偶数=偶数,奇数个奇数相加为奇数可知,s只可能为偶数
  • 综上,$y_2=y_1$

n个奇数相加结果的奇偶性的讨论

方法1

• $s=a_1+a_2+\cdots +a_n=\sum _{i=1}^n{a}_i$

  • $a_i=2n_i+1,n_i\in \mathbb{Z}$

  • $s=\sum _{i=1}^{n}2n_i+\sum _{i=1}^{n}1=2(\sum _{i=1}^n{n}_i)+n$

  • 显然,$2\sum _{i=1}^s{n}_i$是偶数,则s的奇偶性取决于n

  • 因此当n为奇数时,结果为奇数,否则为偶数

方法2

• 首先:
  • 奇数+奇数=偶数
  • 偶数+奇数=奇数
    • 也就是说,数A加上一个B,结果C的奇偶性和A的奇偶性相反,每加一个奇数,结果的奇偶性就取反(改变)一次
    • 因此,将A的奇偶性记为P,(对P取反相当于改变奇偶性)
    • A加k次奇数,
      • 若k是奇数,则相当于对P取反奇数次,结果的奇偶性和P相反
      • 若k是偶数,则结果相当于对P取反偶数次,结果的奇偶性和P相同
    • 这个思路也可以证明上述结论

总结🎈

• 给定任意一个二进制串,求它们的异或,关键要看1的个数,

  • 如果1的个数为奇数,那么结果为1

  • 否则,该结果位上的亦或结果为0

    • 如果只有0没有1,则认为1的个数是0(归属于1的个数是偶数的情况)

计算模二乘/除

• 在模二乘法时,您可以用上述异或运算的结论快速完成计算:
  • 将1的个数为偶数的列对应的结果为写为0,
  • 其余位都用1补齐(分批处理)

实例

乘法

• $$\begin{array}{rc}& 1010\\ \times & 101\\ & 1010\\ & 0000\\ & 1010\\ & 100010\end{array}$$

  • s1			1	0	1	0
    s2		0	0	0	0
    s3	1	0	1	0
    $r_0$(可选)	1				1
    $r_1$(可选)		0	0	0		0
    result	1	0	0	0	1	0

  • 由于模二加/减运算不用考虑进位/借位,所以可以向上面那样列表处理

除法:

• 												1	0	1
  								101	$)$	1	0	0	0	0
  										1	0	1
  											0	1	0
  											0	0	0
  												1	0	0
  												1	0	1
  													0	1

  • 表格中,

    • 不带下划线的是部分余数(或者最开始的被除数)

      • 被除数记为$S=10000$,除数记为$D$=101
      • 除数的位数为d=3位

    • 有划线的表示本位商乘以除数的乘积,称为nextProd

      • 所谓的本位商就是根据部分余数的最高位上商
      • 商记为$Q=q_k,\cdots ,q_1,q_0$的第i位记为$q_i$
      • $nextProd=q_i\times D$

    • 当部分余数位数少于除数的位数,停止计算(结束)

CRC基本信息

• 循环冗余码(Cyclic Redundancy Code)

  • 也称为多项式码

• 任何一个由二进制数位串组成的代码都可以和一个只含有0和1种系数的多项式建立一一对应的关系

• 一个$k$ bit的帧M=M(x)可以视为$X^{k-1}\cdots X^0$的$k$次多项式

  • 如果给定二进制位串M=$m_{k-1},\cdots ,m_1,m_0$

  • 这个多项式的阶数为$r=k-1$

  • 这一点类似于二进制按权展开转化为十进制值

  • $$\begin{gathered} M=M(x)=\sum _{i=1}^{k-1}{m}_i{X}^i \\ {m}_i=0或1 \end{gathered}$$

  • 例如:

    • $M=1110011$,位数k=7;表示为多项式就是$M(x)=X^6+X^5+X^4+0+0+X^1+X^0$
    • 也可以列表填充

  • 例如:

    • $M(x)=X^5+X^4+X^2+X$

    • $阶数r_M=5$

    • 对应的二进制位串长度为k=r+1=6

      • 从成分上也可以直接看出M串中含有4,个1,k-4=6-4=2个0

    • M(x)的各个项(权)	5	4	3	2	1	0
      M(系数序列)	1	1	0	1	1	0

      • $M=110110$

生成多项式

• 生成多项式与其对应的二进制代码之间的关系

  • 生成多项式中各项的系数收集起来就是该生成多项式的二进制代码(将作为模二除法的除数)

    • 如果某一阶对应的项缺失,表示该项对应的系数(二进制代码)为0,
    • 如果存在,则为1

• $$G(x)=1011=1\times x^3+0\times x^2+1\times x^1+1\times x^0=x^3+x+1$$

• 给定一个m bit的帧或报文，发送器生成一个r bit的序列，称为帧检验序列(FCS)

• 这样所形成的帧将由m+r比特组成。

• 发送方和接收方事先商定一个多项式G(x)(最高位和最低位必须为1)，

  • 使这个带检验码的帧刚好能被预先确定的多项式G(x)整除
  • 接收方用相同的多项式去除收到的帧，如果无余数，那么认为无差错

• 带有r个bit的FCS的多项式编码可以检测到所有长度小等于r的突发性错误

• CRC校验可以用硬件完成

计算FCS

• 假设一个帧有m位，其对应的多项式为G(x),则计算冗余码的步骤如下：
  • 1)加0
    • $假设G(x)的阶为r_G,后续r默认都指的是生成多项式G(x)的阶$
      • 而不是M(x)的阶
    • 在帧的低位端加上r个0,将结果数据串记为$L_r$
  • 2)模2除
    • 利用模2除法，用G(x)对应的数据串G去除数据串$L_r$，得到的余数即为冗余码(共r位，前面的0不可省略)。
• 多项式以2为模运算
  • 按照模2运算规则，加法不进位，减法不借位，它刚好是异或操作
  • 乘除法类似于二进制的运算，只是在做加减法时按模2规则进行

例🎈

• 冗余码的计算举例：
  • $设G(x)=1101(即阶数r=3),$
    • $记G(x)的位数为L,那么通常阶数r=L-1$
  • 待传送数据M=101001(即被除数位数m=6)
    • $L_r=M\times 2^r$
    • $L_r=101001,000$
      • 即,从M尾部拼接r=3个0
  • 经模2除法运算后的结果是：
    • Q=$L_{r}mod2divG(x)\cdots R$
    • 商Q=110101（这个商没什么用），
    • 余数R=001
  • 所以发送出去的数据为101001,001(即$2^{r}M+FCS$),共有m+r 位

CRC实例

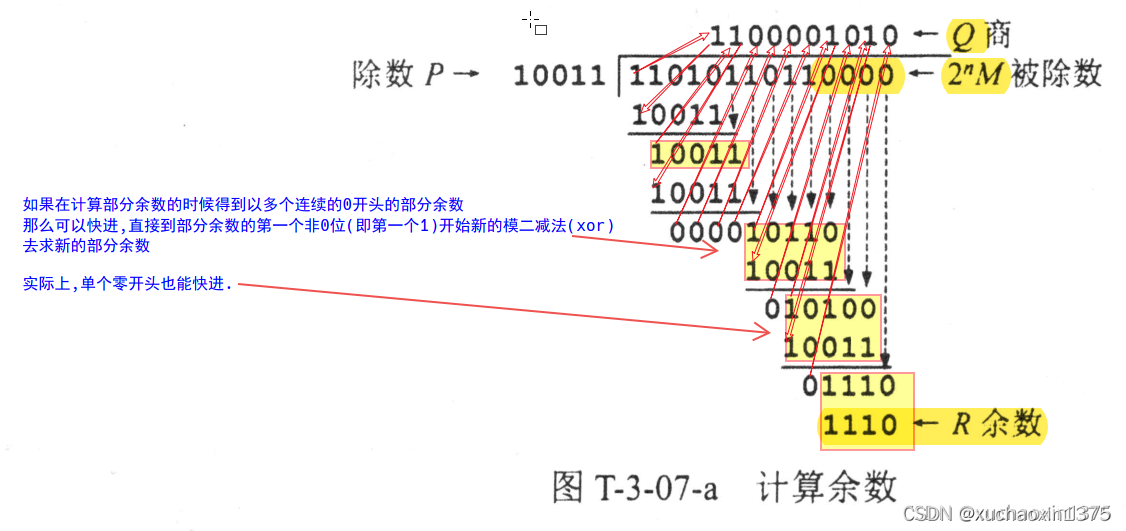
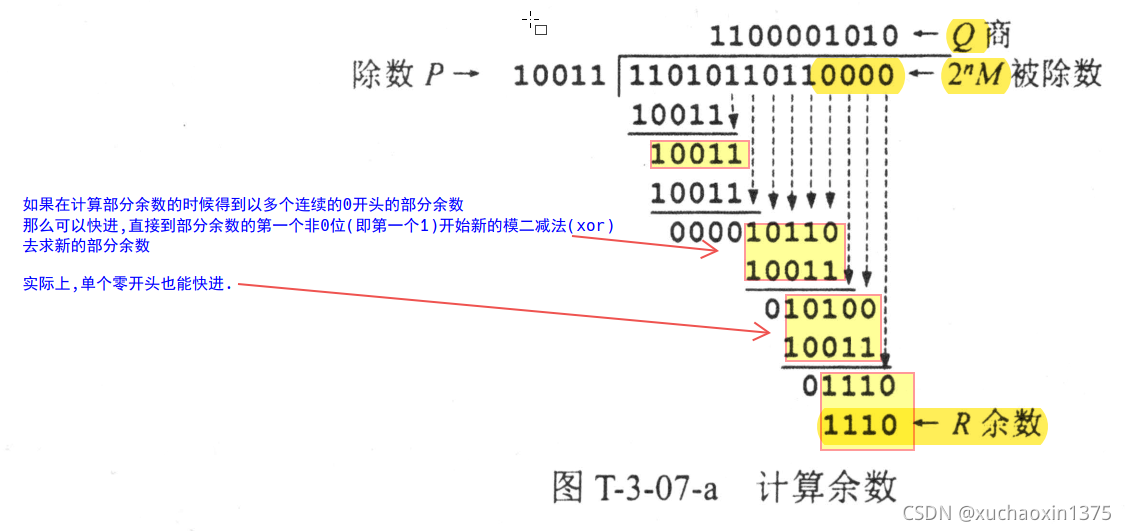
模二除法快进特点(实例)🎈

• 快进到非0位
  • 在第三次上商的时候,您将发现快进
  • 根据前面的分析,每次求新的部分余数都可以执行一定程度的前进
  • 设除数的位数为d=5位
  • 下一次上商之前,从部分余数的第一个非0位开始(第一个1,这个1前面有w个0),继续下放知道凑足d=5位,
  • 继续上商
    • 先补上w个0
    • 在上1(按照一般情况的基本规则继续计算)
    • 基本原理在于前面提到的,每确定一位商,部分余数的位数(高位就会少1位)
      • 相应的,部分余数高位减少w位,也应该确定下来w位的上🎈
    • 不过快进归快进,减法的时候,只有第一位不写,其他的0都要写!

例

• 要发送的数据是M=1101011011，采用CRC校验，生成多项式G(x)是10011，那么最终发送的数据应是（C）。
  • A.11010110111010
    B.11010110110110
    C.11010110111110
    D.11110011011100
  • 经过计算
    • $r=r_G=5-1=4$
      • 生成多项式G(x)的阶为4
    • FCS通过对M做G(x)=10011的模二除法,得到其
      • 余数为R=1110
      • 商Q=11 0000 1010(不关心,只留作草稿)
    • $发送端数据CRC=2^{r}M+R$

帧检验序列FCS(Frame Check Sequence)

• 在选用CRC检测法时

• 上例中的最终余数010即为帧检验序列FCS(也叫冗余码)

ref

• 

设计CRC生成多项式的原则

来自wiki 百科