概率论的学习和整理--番外12：2个概率方案，选择哪个好？如何比较-CSDN博客

下面这是错的！

这种简单思维，完全没有考虑到递归的影响，绿色还可以继续再来合成，需要折算

方案1

3A=1/4*(3+1)+3/4*3 '这里这个1是可以继续再合成的，进行递归合成，无限次
3A=4/4+9/4
3A=13/4

方案2

3A=9/10*3+1/10*6
3A=27/10+6/10
3A=33/10

比较

E(X1)-E(X2)=11/4-33/10=（110-132）/40= -22/40= -11/20

3.2 正确算法1，直接解方程

方案1

解方程，算二者关系

把A视为A, 把B视为B，每3个A可以合成一次B

3A=3/4*B+1/4*(B+A)
11/4*A=B
A=4/11*B

方案2

3A=9/10*B+1/10*2B
3A=11/10*B
A=11/30*B

比较

E(X1)-E(X2)=4/11-11/30= (120-121) /330 = -1/330

3.3 正确算法2，用条件期望求解

把A视为E(X), 把B视为1，每1个A只相当于1/3个B

使用条件期望，先要考虑清楚，要考察的随机变量
这里令 X=是生成B的数量
因为把合成公式用这个视角带入
方案1： 3E(X)=3/4*1+1/4*(1+E(X))
方案2： 3E(X)=9/10*1+1/10*2

因为把合成公式用这个视角带入，但可以只看1个材料合成的情况，1/3即可
其实，其实是用1个A，3个A，或者12个A都可以的，最后都可以约掉
方案1： E(X)=3/4*1/3+1/4*(1/3+E(X)/3)
方案2： E(X)=9/10*1/3+1/10*2/3

如果条件期望计算

方案1

E(X)=1/4*1/3（1+E(X)）+3/4*1/3
E(X)=1/12*（1+E(X)）+3/12
E(X)=4/11

方案2

E(X2)=9/10*1/3+1/10*2*(1/3)
E(X2)=3/10+2/30
E(X2)=11/30

比较

E(X1)-E(X2)=4/11-11/30= (120-121) /330 = -1/330

3.4 算法3，用递归--等比数列求和来算

用递归的方法算

考虑到递归的影响，绿色还可以继续再来合成，需要折算

考虑递归--用等比数列求和的方式算

方式1

需要根据现在的合成关系，去展开
然后去观察下，每次迭代之间的数值关系
确实是符合等比数量
找到公比，后来就好计算了
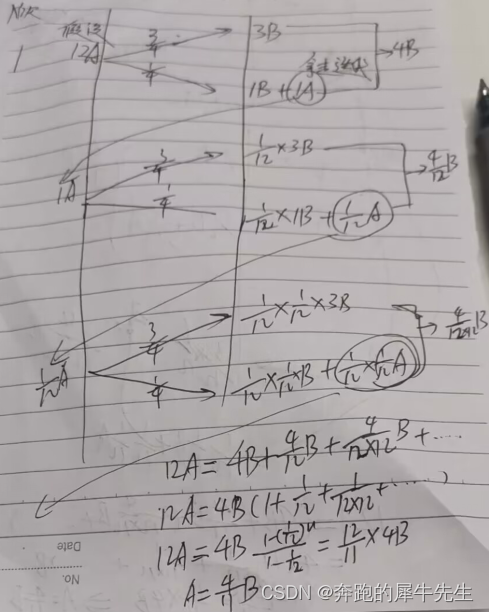
12A =lim 4B+4B/12+4B/12/12+....
12A =等比数列求和
12A =lim 4B*(1-(1/12)^n)/(1-1/12)
12A =4B*12/11
A =4/11*B

方式2

这个不用递归

因为没有涉及到合成后又生成A的问题

3A=9/10*B+1/10*2B
3A=11/10*B
A=11/30*B

比较

E(X1)-E(X2)=4/11-11/30= (120-121) /330 = -1/330