目录
1.1 均匀随机的公式 rand() 和 randbetween()
1.3 如果强行给这些数据添加相同的对应概率,又可以看作均匀分布
2.3 例子3:一个数列,统计其不同数出现的频度可以统计其出现次数的概率
2.5 例子5:有限离散的均匀分布(=等概率分布 =古典概型)
2.7 结论: 数列只是数列,只有带概率信息且概率相等的数列才是均匀分布
0前言
- 虽然说均匀分布很简单,但是,均匀分布函数等等,全整明白也不是那么简单
- 离散的均匀分布和连续的均匀分布还有比较大的区别
0.1 古典概型
古典概型,就是等概率分布,就是指:
有这么一种随机试验,它的所有可能的结果(基础事件)发生的概率是相等的。
0.2 为什么这么多等概率分布/均匀分布?
其实很多现实里的随机试验都不是等概率的,比如常见的硬币,骰子。
这些其实是我们简化问题,做了一些理想假设:
- 硬币=假设是质量厚度均匀的概率
- 骰子=假设是质量均匀的骰子
- 等等
0.3 等概率/均匀分布其实是一种理想假设,或者最初假设
- 我们对一个事物不了解时,获得信息很少时,一般都假设时等概率分布
- 所以这个分布才会很常用。
0.4 伯努利试验,伯努利分布,二项分布
- 伯努利试验,强调的是可以 稳定,相互独立的进行一组随机试验,就是做N次,试验内部不受影响,试验内部基础概率等还是稳定不变的。
- 伯努利分布,0-1分布,就是n=1次伯努利试验,事件A发生的次数
- 二项分布,就是n次伯努利试验,事件A发生的次数
0.5 伯努利试验和等概率模型的关系
- 应该说两者没有直接关系
- 符合其定义的才是
- 一个强调,概率一直相等,无论模型是否稳定
- 一个强调,模型稳定,每次试验独立,不需要是等概率
如果非要联系一下,就是
- 等概率模型里,如果是硬币,骰子这种本身试验内部很稳定,不会变化
- 等概率模型里,如果是拿球不放回试验,也是伯努利试验
0.6 有误导的名称
- 有误导的名称
- 均匀分布,不如叫 等概率分布更准确
- 最小二乘法,不如叫 最小平方法更准确
1 在EXCEL里生成一组随机数
1.1 均匀随机的公式 rand() 和 randbetween()
EXCEL里的rand() 函数可以生成 [0,1)的随机数
- rand() 生成的是 [0,1)的随机数
- randbetween()生成的是[a,b]的随机数
- rand()
- randbetween()
- RAND()*(b-a)+a
- RAND()*(b-a+1)+a
- INT(RAND()*100)

EXCEL默认的散点图,基本都是默认第一象限
可以把坐标轴修改下,X轴显示在均值附近比较直观

1.2 问题是:这是均匀分布的一组数吗?
1.2.1 这个数组是均匀分布的吗
- 初看好像是,又好像不是
- 其实并不是,这只是一组随即数,并不是均匀分布的随机数。
- 比如验证均值和方差可以发现,均值和方差和均匀分布的都有差别
结论
- 所以一组随机数只是一组随机生成的数,并非均匀分布的随机数。
- 这组数本身不均匀,也没有对应的概率列,非均匀分布
理想中的0-1均匀分布,rand()生成的也是[0,1)的随机数
均值=(0+1)/2=0.5
方差=0
当然肯定会样本量太少有关系,但是日常用到确实样本量可能很小
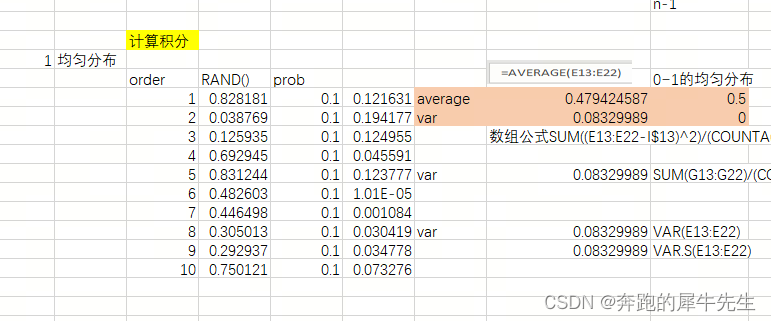
1.2.2 一个数组的均值和方差的求法
EXCEL的内置函数
- 均值,average()
- 方差
- var() var.s() 一定要注意这里都是求的样本方差,也就是分母用的是(n-1)
- var.p() 一定要注意这里都是求的总体方差,也就是分母用的是(n)
直接求法
直接用方差的定义来求,
直接求法注意
- 如果是总体方差,则用总本方差=Σ(x-average())^2/n
- 如果是样本方差,则用样本方差=Σ(x-average())^2/(n-1)
- SUM(G13:G22)/(COUNTA(E13:E22)-1)
- SUM(G13:G22)/(COUNTA(E13:E22)-0)
- 还可以用数组公式SUM((E13:E22-I$13)^2)/(COUNTA(E13:E22)-1)
1.2.3 使用数组公式时的注意点
- 3个公式计算结果完全不同,要注意用括号控制运算次序。
- 第1个=1^2+2^2+3^2=[1,4,9] 但是因为只选择了显示第1个,所以看起来以为是1,其实只是[1,4,9] 的第1个元素
- 第1个=(1+2+3)^2=36
- 第1个=1^2+2^2+3^2=1+4+9=14

1.3 如果强行给这些数据添加相同的对应概率,又可以看作均匀分布
因为原来那个数组,没有概率信息,如果强行加上1条对应的等概率数组,
可以强行认为是均匀分布,设定其概率就好

2 区分几种情况
所以是不是均匀分布,先需要把这些概念厘清
2.0 随机数,XX数列,带概率的数列,均匀分布
- 概念1:随机数,一组随机数
- 概念2:等差数列
- 概念3:带概率的数列,或者能从数列出提炼出频度/权重/概率
- 概念4:离散的均匀分布,不只是等差数列
2.1 例子1:一组随机数
- 只是因为一些需要,随机生成的一组数据(可以指定随机范围)
- 一个随机数,
- 一组随机数特点就是:这些数都在指定范围内随机生成,一般各不相同。和均匀分布没啥直接关系。
2.3 例子2:等差数列 / 等比数列等
- 比如1,2,3,4....10这个是等差数列
- 比如1,3,5,7....11这个是等差数列
- 但是无论是不是等差数列,数列里并没有概率信息,所以只是数列,和概率分布没关系
2.3 例子3:一个数列,统计其不同数出现的频度可以统计其出现次数的概率
- 虽然一般来说,一个数组是没有概率信息的
- 如果是按频度统计为概率,那么保证每个数出现的次数相同也是可以的
- 但这么做,相当于强行给数列,增加了一组映射的列信息。
- 但是,概率本身是可以来源于频度的,如果一个数列里有多个数,可能重复,可以把频度作为权重,进而统计不同的数出现的概率。这样可以统计出一个概率分布来。

2.4 例子4,带概率的数列
- 如果一个数组,同时数组中的每个数还对应着概率,那么这就是一个概率分布
- 可以全手动设定
- 均匀分布的特点是,概率相同,所以事件本身取值是无所谓的,手动随便写10个数,然后设定其概率相等也是一样
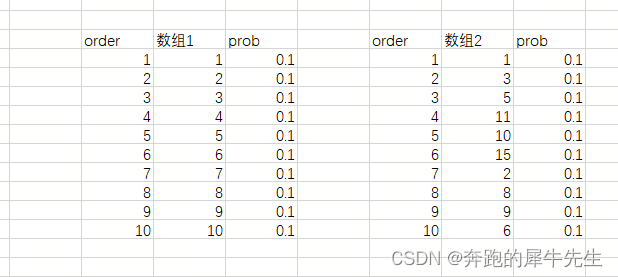
2.5 例子5:有限离散的均匀分布(=等概率分布 =古典概型)
- 可以是等差数列,比如1,2,3....10
- 可以是等比数列,比如1,2,4....512
- 甚至可以是没规律的数列,但是概率都相同
- 可以是任何数,只需要这些数/内容,对应概率相等即可。因此就是等概率分布

- 离散的数列也分为有限和无限。
- 这里先不讨论无限的离散数列的情况。
- 如果是有限个数,其实离散的均匀分布 =等概率分布 =也就是古典概型
2.6 连续的均匀分布
- 连续的均匀分布,每个可能的点的概率 p=1/(b-a)
- 而离散的均匀分布,因为只有n个数,每个可能的点的概率 p=1/n ,两者完全不同

2.7 结论: 数列只是数列,只有带概率信息且概率相等的数列才是均匀分布
- 数列只是数列而已
- 有的是等差,等比数列
- 无规律数列
- 一组范围在a,b 之间的随机数数列
- 等等
- 只有带概率信息且概率相等的数列才是均匀分布
- 无论有限还是无限
2.8 数列/数组求均值方差和概率分布的不同
从均值,方差原始定义求即可
- 均值,就是均值的定义方式,average(xi),本身数列也没有概率信息
- 方差,就是均值的定义方式,var(), 使用方差的定义求方差即可
- D=E(X^2)-E(X)^2
- D=Σ(x-aver(x))/n
3 有限离散的均匀分布(=等概率分布 =古典概型)
3.1 定义:概率相等!
- 可以是任何数,只需要这些数/内容,对应概率相等即可。
- 因此就是等概率分布
2个要求
- 1 有限元素的集合
- 2 每个元素的概率相等
百度里这个图狠有误导性,概率相等即可,对数列本身没有要求均匀间隔。

3.2 举例子
- 可以是一组数
- 可以是一组不相同的数
- 可以是一个骰子
- 可以是一个袋子里的不同的球
3.3 连续分布的这2个公式,不适合离散的连续分布
3.3.1 下面这2个公式,都只适合 连续的均匀分布
- 数学期望:E(x)=(a+b)/2
- 方差:D(x)=(b-a)²/12
- f(x)=1/(b-a)
3.3.2 而如果是离散的连续分布
- 均值,就是均值的定义方式,average(xi),和概率无关(即使加上概率权重,因为概率相同,不同元素的概率权重都相等,还是和概率无关)
- 方差,就是均值的定义方式,var(), 使用方差的定义求方差即可
- D=E(X^2)-E(X)^2
- D=Σ(x-aver(x))^2/n
- 概率密度函数
- f(x) =1/n
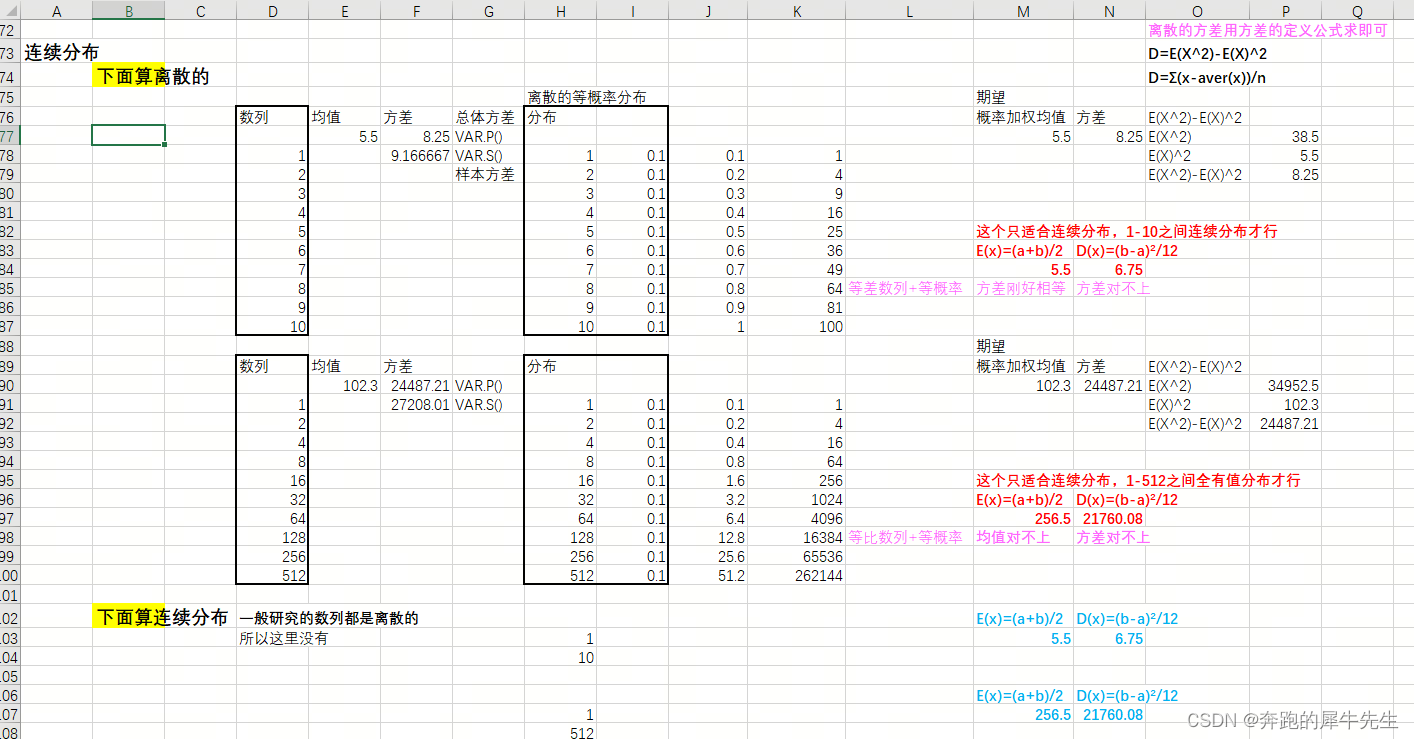
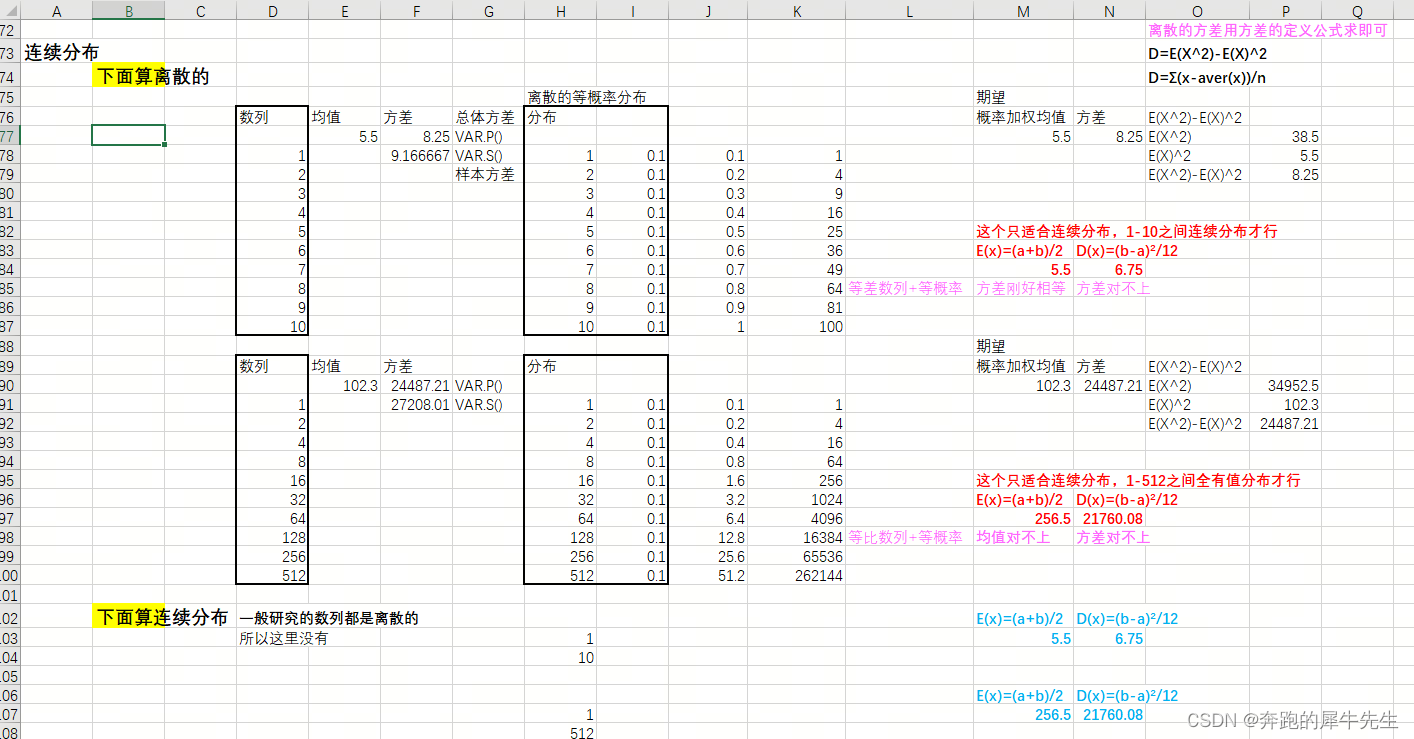
3.4 计算均值
因为是等概率
均值,就是均值的定义方式,average(xi),和概率无关(即使加上概率权重,因为概率相同,不同元素的概率权重都相等,还是和概率无关)
E(X)=概率加权平均值=average(xi)
3.5 计算方差
- 方差,就是均值的定义方式,var(), 使用方差的定义求方差即可
- D=E(X^2)-E(X)^2
- D=Σ(x-aver(x))/n
4 连续的均匀分布
4.0 离散和连续的均匀分布,对比差别
均匀分布,概率不应该是平均分吗?
离散型是这样
- bi比如有10个,那就是每个概率都=1/10
- bi比如有100个,那就是每个概率都=1/100
- 离散的 用概率 1/个数
如果是连续的呢
- b-a 有多长,
- 概率就用全部概率1 去除以 1/(b-a)
- 因为b-a里理论无限个点
- 只能算b-a的长度
- 均匀分布的均值为(a+b)/2,方差为(b-a)^2/12。

4.1 什么是连续的均匀分布

4.2 连续分布的这3个公式
- 数学期望:E(x)=(a+b)/2
- 方差:D(x)=(b-a)²/12
- var(x)=E[X²]-(E[X])²=1/3(a²+ab+ b²)-1/4(a+b)²=1/12(a²-2ab+ b²)=1/12(a-b)²
- f(x)=1/(b-a)
4.3 求连续分布的均值/期望和方差
4.4 方差和均值的公式的推导

4.5 如何对连续均匀分布求积分

积分的求法
- ∫a,b f(x)Xdx
- ∫a,b (1/(b-a))Xdx
- 1/(b-a)∫a,bXdx
- (1/(b-a))*X^2/2+C
求积分的2个端点对应积分值,分别带入a ,b
- 带入b (1/(b-a))*b^2/2+C
- 带入a (1/(b-a))*a^2/2+C
这部分积分内容
- 上面两者相减
- (1/(b-a))*(b^2/2-a^2/2)
- (1/(b-a))*(b^2-a^2)/2
- (1/(b-a))*(b^2-a^2)/2 ’
- 其中,因为(b+a)*(b-a)=b^2-a^2
- (1/(b-a))*(b-a)(b+a)/2
- (b+a)/2
因此,积分结果
∫a,b f(x)Xdx= (b+a)/2
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








