动态规划

星型结构的动态规划

$$图1. 归一化的人脸图像$$

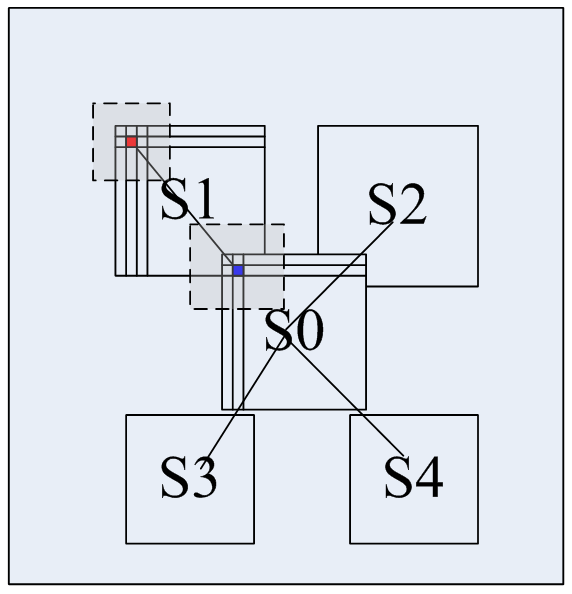
其中,$S0,S1,S2,S3,S4$分别是$cen, lel,rer,ml,mr$,（即中心，左眼眼角，右眼眼角和嘴左角，嘴右脚）是搜索空间。
红色的点和蓝色的点之间的连线称之为：$spring$，其外围的虚线边框是该特征点对应的$patch$.

动态规划问题：

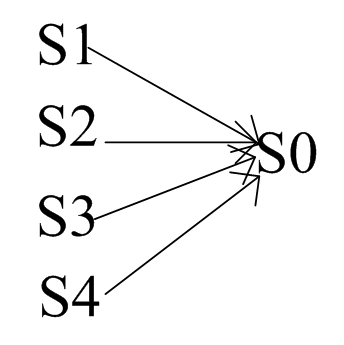
注：下面$S0-S4$即表示搜索空间，又表示阶段。采用混合术语。
1阶段
这里从$S0,S1,S2,S3,S4$可以看作1-5阶段。
2状态
第一个阶段S0的状态变量，即$cener$，或用$s_0$表示，其状态变量的集合即为搜索空间，图中S0所标注的矩形区域。
3决策
状态变量$lel$取值为红色的位置时，其下一个阶段，可以选择蓝色的位置，或者蓝色的前一个位置。这表示决策。描述决策的变量称为决策变量。如从第二个S1阶段到第一个阶段S0决策的例子：
$u_1(lel='红色位置')$，可以看作是一个决策变量，其取值是整个S0区域。
编程时，通常定义一个决策数组，用来跟踪状态的变化，用来寻找达到最优时的最优策略。
4策略
各决策阶段组成的序列就是策略。我们的目的是根据一个”评价函数+准则”，找到最优的策略。
5状态转移方程
其描述了上一个阶段的状态$s_k$和下一个阶段的状态$s_{k+1}$，以及决策$u_k$的关系，如上为：

$$s_{k+1}=u_k(s_k)$$
6指标函数
即评价函数。即我们希望找到的5个landmarks满足，所有特征点的纹理匹配代价和形变代价最大。

纹理代价：
我们可以提取hog,sift,sparse_LBP,LBF等特征。在评价函数一般确认的情况下，纹理特征的描述和提取对于landmarks的定位很重要。学过模板匹配的都知道，当检测的区域的纹理特征和模板表示的特征相同时，可以达到最大的响应。
形变代价：
常用的代价是两个特征点之间的位移矢量的二次函数,则两个特征点之间的形变代价为：。

$$f((x_i,y_i),(x_j,y_j))=a(dx)^2+b(dx)+c(dy)^2+d(dy) \qquad (2)$$
其中 $a,b,c,d$是在训练时，需要学习的模型参数。
在模型的学习过程中，我们只要约束二次函数的二次项的系数全负，我们就可以利用广义距离变换加速动态规划的求解。

辅助理解：

文献1中，公式（3）

$$Shape_m(L)=\sum_{ij \in E_m}{a_{ij}^mdx^2+b_{ij}^2+c_{ij}^mdy^2+c_{ij}^mdy^2+d_{ij}^mdy} \qquad(3)$$
其中 $m$表示component 或者viewPoint或者mixture，即视角
$ij\in E_m$表示 $i,j$相连。
上述公式转换为公式（4）：
$$Shape_m(L)=-(L-\mu_m)^T\Lambda_m(L-\mu_m)+constant \qquad(4)$$
其中 $(\mu,\Lambda)$是形状参数 $(a,b,c,d)$重新参数化的表示。其类似于一个高斯分布。其中 $\Lambda_m$是一个sparse precision matrix，即其中的非0项对应于 $E_m$中相连的两个部分 $i,j$。[34]给出，当二次函数的 $a,c$两个系数是负的时，矩阵 $\Lambda_m$是正定的。 $\mu_m$可以看作是理想的形状。 $\Lambda_m$小的特征值对应的特征向量表示带有小惩罚的“形变模式 deformation mode”。
个人理解：当 $\Lambda_m$正定时，则：
$$-(L-\mu_m)^T\Lambda_m(L-\mu_m)<0$$
同时公式(2)对于二次是一个抛物面，开口向下的抛物面。其正迎合了广义距离变换的求解。
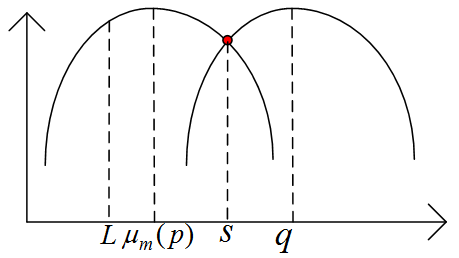
评价函数：
$$f(L)=App(L)+Shape(L)$$
我们希望评价函数值越大越好，对于纹理，越匹配，则 $App(L)$值越大。对于 $Shape(L)$也是约匹配的时候越大。（下图，抛物线画的不标准，广义距离变换在求解时，需要两个抛物线的交点只有一个。我们将形变和广义距离变换画在同一个图上了，其中 $L$表示当前形状，$\mu_m$表示理想的形状， $p,q$表示一维网格，其对应图中的两个抛物线， $S$是两个抛物线的交点。）

1.欧式距离的广义距离变换：

给定$G=\{0,...,n-1\}×\{0,...,m-1\}$是一个二维的网格，并且 $f:G\rightarrow R$是网格上的任意函数。函数 $f$的二维距离变换（在平方欧式距离下）给出：

$$D_f(x,y)=\min_{x',y'}\big((x-x')^2+(y-y')^2+f(x',y')\big)\quad (5)$$
这里，$(x,y)和(x',y')在同样的网格上。$
和多元函数求解积分类似，由于公式（5）中的第一项不含有 $y'$，那么我们可以对公式（5），先对 $y'$最小化，或者先对 $x'$最小化：
先对 $y'$：
$$D_f(x,y)=\min_{y'}\big((y-y')^2+\min_{x'}\big((x-x')^2+f(x',y')\big)$$
$$=\min_{y'}\big((y-y')^2+D_{f|y'}(x)\big)\quad(6)$$
先对 $x'$：
$$D_f(x,y)=\min_{x'}\big((x-x')^2+\min_{y'}\big((y-y')^2+f(x',y')\big)$$
$$=\min_{x'}\big((x-x')^2+D_{f|x'}(y)\big)\quad(7)$$
说明：例如上式，先对将 $x'$看成常数，对 $y'$进行最小化、

2.任意二次形变函数的广义距离变换：

公式（3）中，我们针对某两个相邻的landmarks，如果从$V_i\rightarrow V_j$，我们称$V_i$为孩子，$V_j$为父亲，进行动态规划求解，即形如公式（2）那样：

$$f(x_j,y_j)=\max_{x_i,y_i}\big(f(x_i,y_i)+f((x_i,y_i),(x_j,y_j))\big)=\max_{x_i,y_i}\big(a(dx)^2+b(dx)+c(dy)^2+d(dy)+f(x_i,y_i) \big)\quad (8)$$
其中 $f(x_i,y_i)$表示孩子基准点匹配的纹理代价, $f((x_i,y_i),(x_j,y_j))$表示两个基准点之间的形变代价。
同理，我们也可以转换为一维广义距离变换：
$$f(x_j,y_j)=\max_{x_i}\big(a(dx)^2+b(dx)+\max_{y_i}(c(dy)^2+d(dy)+f(x_i,y_i) )\big)\quad (9)$$
即：
$$f(x_j,y_j)=\max_{x_i}\big(a(dx)^2+b(dx)+\max_{y_i}(c(dy)^2+d(dy)+f(x_i,y_i) )\big)\quad (10)$$

其实现过程中，只需要修改交叉点$s$的计算，以及$D_f(x_j,y_j)$的计算。

在图1中的$S1\rightarrow S0$的动态规划的计算，可以将搜索区域$S1和S0$都映射到从1(for matlab)或者从0(for C)开始的位置，即通过减去各搜索区域的左上角位置。然后直接利用文献2中的一维广义距离变换求解。

算法复杂度的分析：

常规遍历算法的时间复杂度：

针对图1中$S1和S0$，我们假设S1区域大小为$h_1×w_1$，S0的搜索区域为$h_0×w_0$，则外循环次数为$h_0×w_0$,内循环次数为$h_1×w_1$，则
时间复杂度为：

$$O(h_1×w_1×h_0×w_0)$$

广义距离变换的时间复杂度：

1.计算下包络（lower envelope或上包络）时间复杂度为：$h_1×w_1$
2.填充值（查找表）时间复杂度为：$h_0×w_0$
故总的时间复杂度为：

$$O(h_1×w_1+h_0×w_0)$$

参考文献：

1、Face Detection, Pose Estimation, and Landmark Localization in the Wild
2、Distance Transforms of Sampled Functions（广义距离变换）