基于隐马尔可夫模型的有监督词性标注

词性标注（Part-of-Speech tagging 或 POS tagging)是指对于句子中的每个词都指派一个合适的词性，也就是要确定每个词是名词、动词、形容词或其他词性的过程，又称词类标注或者简称标注。词性标注是自然语言处理中的一项基础任务，在语音识别、信息检索及自然语言处理的许多领域都发挥着重要的作用。

       词性标注本质上是一个分类问题，对于句子中的每一个单词W，找到一个合适的词类类别T，也就是词性标记，不过词性标注考虑的是整体标记的好坏，既整个句子的序列标记问题。对于分类问题，有很多现成的数学模型和框架可以套用，譬如HMM、最大熵模型、条件随机场、SVM等等，在本博客中我们介绍基于隐马尔可夫模型（HMM）的词性标注。

1 隐马尔可夫模型（HMM）

       隐马尔科夫模型(HMM)是什么？说白了，就是一个数学模型，用一堆数学符号和参数表示而已，包括隐藏状态集合、观察状态集合、初始概率向量, 状态转移矩阵A，混淆矩阵B。

       在wiki上一个比较好的HMM例子，浅显易懂地介绍了HMM的基本概念和问题，初次接触HMM的人可以首先看一下这个例子。在Hidden Markov Models网站，更加详细地介绍了HMM，在此我们借用该网站中的例子和图进一步介绍HMM。

       想象一个这样的场景：一个诗人因为抨击当权派被打入地牢中，在暗无天日的地牢中诗人不想无所事事，整日沉沦，所以他每天都在墙上写诗抒发情感。某日，他在地牢的墙角发现一些苔藓。在毫无生机的地牢里能发现另一种生命让他深感欣慰，每天都与苔藓对话。几天之后他发现一个现象，苔藓有时湿润，有时干燥，他猜想这可能和外面未知的天气有关。

       根据上面的描述，我们可以构造一个HMM，然后利用苔藓的状态来预测天气。首先，天气是未知的状态，是需要推测的量，在HMM中就是隐藏状态。为了简化起见，假设诗人被捕的地牢外面只有三种天气状态：晴天（Sun）、雨天（Rain）和阴天（Cloud），如图一所示。

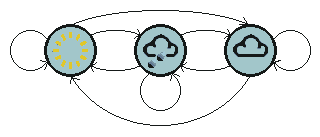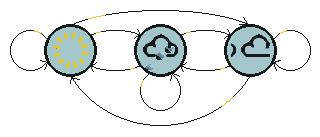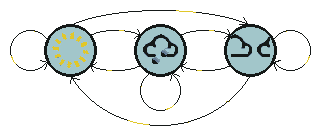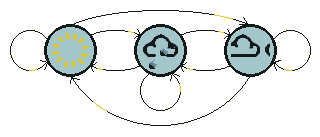
图一 天气状态转换图

       状态转换可以分为确定型的和非确定型的，交通灯的状态转换是确定型的，也即在红灯之后我们肯定知道下一个状态是绿灯。但是天气状态的转换是非确定型的，也即今天是晴天，不能确定明天是什么天气（即使现在的天气预报非常准确，我们还是无法100%知道明天的天气，其实明天的世界有很大的不确定型）。不确定型的状态转换需要采用概率模型来描述它们之间的状态变化。图二描述了地牢外面天气的状态转移矩阵：

图二 天气的状态转移矩阵

       上述矩阵是行随机的（row stochastic），每一行的概率相加是1，含义是不管昨天什么天气，今天肯定是（sun,cloud,rain）天气中的一种，只是每一种天气发生的概率不同。假设有N个状态，隐藏状态的状态转移矩阵就是一个N*N的矩阵，通常称为A。

       此外，我们还需要一个不同天气发生的先验概率，也即地牢外面常年统计获得的三种天气发生概率，通常称为 。假定（sun,cloud,rain）发生的先验概率为：

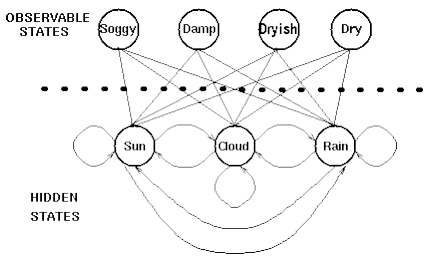
现在我们已经有HMM的两个参数，还缺一个关于观测状态的参数。在地牢中，诗人可以观测的量只有苔藓的状态，为简化起见，假设苔藓的变化只有四种状态：非常潮湿（Soggy）、潮湿（Damp）、干燥（Dryish）和非常干燥（Dry）。这些可观测的状态都和隐藏的天气相关，如图三所示。每一个隐藏的天气状态都可能会产生苔藓的四种状态，又只是概率不同而已。为了描述这个概率，需要引入一个混淆矩阵（confuse matrix），又叫发射矩阵。用来描述不同天气状态下产生苔藓不同状态的概率，如图四所示。

图三 隐藏天气状态和观测状态之间的关系

       混淆矩阵描述了HMM的第三个参数，通常称为B。假定有M个可观测状态，则混淆矩阵是N*M的矩阵，并且每一行的概率为1，表示在某个天气状态下，苔藓肯定属于（Soggy，Damp，Dryish，Dry）中的一种状态。

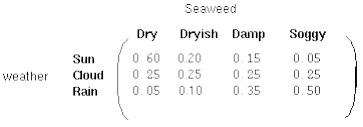
图四 HMM的混淆矩阵

       整个HMM就是由上述三元组构成，可以用HMM表示。知道了这三个参数，我们就可以完全了解整个HMM。HMM可以用来解决三个问题：

1. 给定一个模型，如何计算某个特定的观测序列的概率；
2. 给定一个模型和某个特定的观测序列，如何找到最可能产生这个输出的隐藏状态序列；
3. 给定足够的观测数据，如何估计HMM的三个参数。

       在语音识别领域，主要关注第一和第三个问题，在词性标注中主要关注第二和第三个问题。解决第一个问题的用途是：在有多个HMM的情况下，选择使概率最大的HMM。在语音识别领域，需要对每个词构建一个HMM模型，就将语音识别成概率最大的HMM对应的词。解决第二个问题的用途是可以知道观测序列最有可能的隐藏状态序列，词性标注就是解决这个问题。第三个问题对所有应用HMM的人来说都非常重要，但是也最难，也即训练模型参数。HMM的三个参数并不是凭空想出来的，而是训出来的。

       第一个问题可以通过前向算法快速解决，第二个问题需要利用Viterbi算法解决，第三个问题则有两种方法解决：有监督或者无监督。有监督的参数训练通过标注训练集统计获得相关参数，难度较低；无监督的参数训练则通过鲍姆-韦尔奇算法迭代训练获得，难度很大。在此我们介绍有监督的词性标注，也即HMM参数的训练通过统计语料库获得。

2 词性标注

       词性标注的目的就是对给定的句子先分词，然后给每一个词标注不同的词性。很明显可以看出，HMM中的可观测序列就是词性标注中给定句子的分词，而隐藏状态就是不同的词性，词性的先验概率即是参数所以，为了实现对句子的词性标注，我们需要首先利用语料库训练一个HMM，然后再对句子进行分词和标注。

2.1 中文分词

       我们首先介绍中文分词。这是因为用户输入的是一个完整的句子，并不能直接得到可观测序列。采用统计语言模型的中文分词，效果已经非常好，可以认为中文分词是一个已经解决了的问题。不过，这又需要训练一个新的马尔可夫模型，不属于本博客考虑的范围。在此，我们实现了一种最简单的中文分词：总左往右扫描句子，然后查找词库，找到最长的词匹配，遇到不认识的字串就分割成单字词。

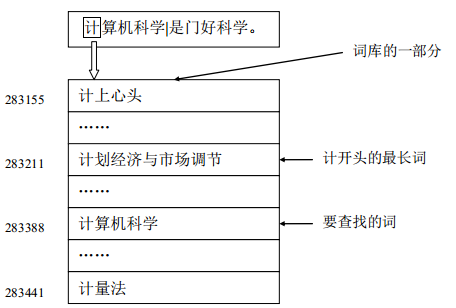
       在代码中，我们有一个接近35w的词库，词库中的词语按照unicode码排序，可以方便地查找。在分词时，首先将词库读到内存中，然后将句子按照从左往右最长匹配原则查找词库。由于词库按照unicode码排序，所以我们可以采用二分快速查找词组。查找时，我们首先读取原始句子的第一个字，定位到该字在词库中的起始位置和结束位置，然后进行二分查找即可。在查找的过程中记录起始和结束位置之间所有词的最大长度，然后从最大长度开始查找词库，长度逐一递减，直到找到为止。图五简单描述了分词的过程：

图五 中文分词示意图

2.2 HMM参数训练

       HMM需要训练的参数有三个，即。表示词性的先验概率，A表示词性之间的状态转移矩阵，B表示词性到词的发射矩阵或者混淆矩阵。本博客采用有监督的方式训练上述三个参数。有监督的方式，也即通过统计语料库中的相关信息训练参数。图六是我们采用的语料库的部分截图，每一行都是一个完整的被标注过的句子。

图六 部分语料库

       HMM参数训练就是通过分析上述语料库获得HMM的三个参数。通过解析上述语料库我们可以获得：每个词性出现的次数，每个词性及其后继词性出现的次数和词性对应的词。统计完这些信息之后就可以以频率代替概率获得三个参数的值。

       统计上述信息的关键是解析语料库，解析通过下面三句正则表达式完成：

[java]  view plain copy print ?

1. // 获取预料语料库中的一个个不同的词组(以空格分开)，词组后附有相应的词性  
2. text = content.toString().split("\\s{1,}");   
3. // 去除词性标注，只保存词组  
4. phrase = content.toString().split("(/[a-z]*\\s{0,})");//"/"后面跟着一个或者多个字母然后是多个空格  
5. // 获取语料库中从前往后的所有词组的词性  
6. characters = content.toString().split("[0-9|-]*/|\\s{1,}[^a-z]*"); //开头的日期或者空格+非字母作为分隔符  

注释已经详细解释了正则表达式的含义，在此不再赘述。获得上述信息之后，我们就可以很容易地统计相关信息，进而利用频率算概率。词性先验概率的计算没有任何难度。隐藏状态转移矩阵按照公式：

来计算， 表示不同的两个词性前后出现的次数， 表示词性 出现的次数。可观测状态的发射矩阵按照公式：

来计算， 表示某个词和某个词性同时出现的次数。在计算频率的时候，由于有些值非常小，为了避免后面计算过程中的下溢，我们统一将计算的结果乘以100。个人不能保证这种方法的可靠性，事实上，对于频数为零或者频数很小的情况，我们需要按照古德-图灵估计重新计算（数学之美P34），之后求最优隐藏序列需要采用log方式。在此，为了简便，忽略这些细节（不要在意这些细节☺）。假设通过分析语料库，最后获得了N个词性，M个词组，则 就是一个长度为N的向量，A是一个N*N的句子，B就是一个N*M的矩阵。后面对句子进行词性标注时，要确保分词后的词组都在M中，否则就超出了HMM的处理能力。

2.3 再次分词

       一般情况下，完成HMM参数训练之后，我们就可以利用HMM完成一些具体的事情。不过，在这之前对于我们的词性标注系统，还需要进一步分词。我们采用的分词方法是从左往右，最大匹配模式。但是程序中采用的语料库却倾向于最小匹配模式。所以我们初次分词的结果有可能不在语料库中。在此我们将语料库不能识别的词组再次进行分词尝试让算法找到更多的词。

       再次分词的算法很简单。既然我们已经统计了HMM中出现过的所有可观测状态M，则将分词的结果在所有的状态中查找即可。找不到的分词分成两部分作为新的分词。

2.4 Viterbi算法

       终于要说到大名鼎鼎的Viterbi算法了，但是从难度上来说，它远不如模型的参数训练麻烦，所以其实它很简单。为了更数学化的描述该算法，我们先声明几个符号：

• ：隐藏状态的先验概率；
  
• ：隐藏状态的转移矩阵，每一项表示从状态转移到状态的概率；
  
• ：隐藏状态产生观测状态的发射矩阵或混淆矩阵，每一项表示隐藏状态产生观测状态的概率；
  

       在介绍Viterbi算法在计算隐藏状态序列的优越性之前，我们先考虑穷举算法。还是考虑一开始的诗人天气预测问题。假设诗人连续三天观测到苔藓的状态为（dry，damp，soggy），现在要求最可能的天气状态。最简单但是最笨的方法是将三天的所有天气组合罗列出来，然后求每一种组合的概率，选择概率最大的组合即可，如图七所示。

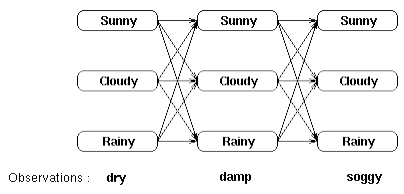
图七 观测序列的所有可能隐藏序列组合

       按照上面穷举算法，最可能的状态序列求法如下：

假定有T个可观测状态，给定一个隐藏状态序列，计算复杂度为O(2T)，所以总的复杂度为O(2TN^T)。显然这个复杂度为指数级，无法应用到实际中，基于动态规划的Viterbi算法应运而生。

既然要求最可能的隐藏状态序列，则其必然满足该序列发生的可能性最大，同时子序列也满足最优子结构： x₀,x₁,…,x_t发生的概率也必须最大，否则可以替换成概率更大的序列，从而产生更好的序列，这与前提矛盾。DP算法有两个关键点：递归方程和初始化。假定我们现在已经求得了最可能发生的前 t个隐藏状态，在求 t+1个状态时，我们需要从第 t个状态中选择最优的一个状态。由于在时刻 t，共有 N个可以选择的隐藏状态，所以 t+1时刻的计算就是从这 N个状态中选择一个使 t+1状态概率最大的。初始化主要是依赖于先验概率。由此可得Viterbi算法的步骤：

1. 令，i=0,1,…,N-1；
   

2. 对t=1,2,…,T-1，i=0,1,…,N-1，计算：

   

3. 在时刻T-1会得到以N个不同状态结尾的概率，选择概率最大的状态：

   

4. 计算最大概率不是目的，目的是要找到使概率最大的隐藏序列，这就需要保存每一步计算过程中选择的最优状态，然后回溯即可。

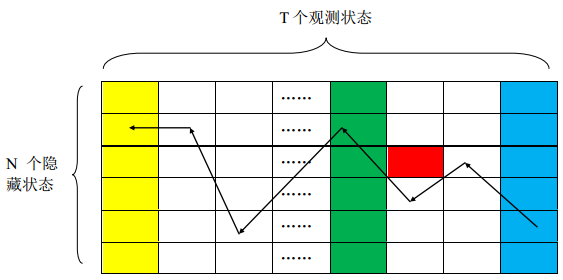
Viterbi算法的计算可以通过图八说明。黄色的一列是需要初始化的列，红色方格的计算依赖绿色的列，最后结果是蓝色列中的最大值。计算完成之后，再通过回溯找到最优的隐藏状态序列。

图八Viterbi算法的矩阵计算过程

       有了Viterbi算法，我们就可以快速获得最优的隐藏序列，由于图八中的矩阵总共有N*T个元素，每个元素的计算复杂度为O(N)，所以总的复杂度为O(TN²)。在实际的实现过程中，我们最好将隐藏状态和观测状态交换一下位置，也即对上述矩阵进行转置，这是因为如果按照图八的方式，每一列元素实际上是不相邻的，这会导致非常严重的cache缺失，从而会使计算性能下降，图示只是为了描述方便才这样画的。

3 总结

       针对词性标注，我们在利用HMM时需要解决两个问题：HMM三个参数的训练和寻找最优隐藏序列。在词性标注领域，存在非常多的语料库，所以我们采用有监督的训练方式获得HMM参数，然后利用Viterbi算法求最优隐藏序列。整个算法的关键在于理解HMM，只有真正理解了，后面的所有任务都可以轻而易举地解决。

4 参考资料

[1] 数学之美3,4,5,26章；

[2] 隐马尔可夫模型；

[3] A revealing introduction to hiddenmarkov models；

[4] HMM在自然语言处理中的应用一：词性标注。