16 树与大顶堆、小顶堆

1、树的描述

由图到树，树的基本概念

树是不包含回路的连通无向图，树有三条性质：

（1） 一棵树中的任意两个结点有且仅有唯一的一条路径连通。

（2） 一棵树如果有n个结点，那么它一定恰好有n-1条边。

（3） 在一棵树中加一条边将会构成一个回路。

树中的每一个点叫做节点，在上面的图中，1号节点为根节点，也成所有节点的祖先，节点2,3,4是1号节点的儿子，1号节点是2，3,4节点的父亲，父亲节点叫做父节点，儿子节点叫做子节点，没有父节点的节点是整棵树的根节点，没有子节点的节点叫做叶节点，比如上图中5 6 7 8 9 10节点，其他的节点叫做内部节点，节点的深度为该节点到达根节点的层数，比如2号节点深度为2,5号节点深度为3.

2、二叉树

二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子，左边的叫做左儿子，右边的叫做右儿子，或者说每个结点最多有两棵子树。更加严格的递归定义是：二叉树要么为空，要么由根结点、左子树和右子树组成，而左子树和右子树分别是一棵二叉树。上面这棵树就是一棵二叉树。 

满二叉树

如果二叉树中每个内部结点都有两个儿子，这样的二叉树叫做满二叉树。或者说满二叉树所有的叶结点都有同样的深度。比如下面这棵二叉树，满二叉树的严格定义为一棵深度为h的且有2^h-1个节点的二叉树。

完全二叉树 

如果一棵二叉树除了最右边位置上有一个或者几个叶结点缺少外，其他是丰满的，那么这样的二叉树就是完全二叉树。严格的定义是：若设二叉树的高度为h，除第h层外，其他各层（1～h-1）的结点数都达到最大个数，第h层从右向左连续缺若干结点，则这个二叉树就是完全二叉树。也就是说如果一个结点有右子结点，那么它一定也有左子结点。例如下面这三棵树都是完全二叉树。其实你可以将满二叉树理解成是一种特殊的或者极其完美的完全二叉树。

其实完全二叉树中父亲和儿子之间有着神奇的规律，我们只需用一个一维数组就可以存储完全二叉树。首先将完全二叉树进行从上到下，从左到右编号。

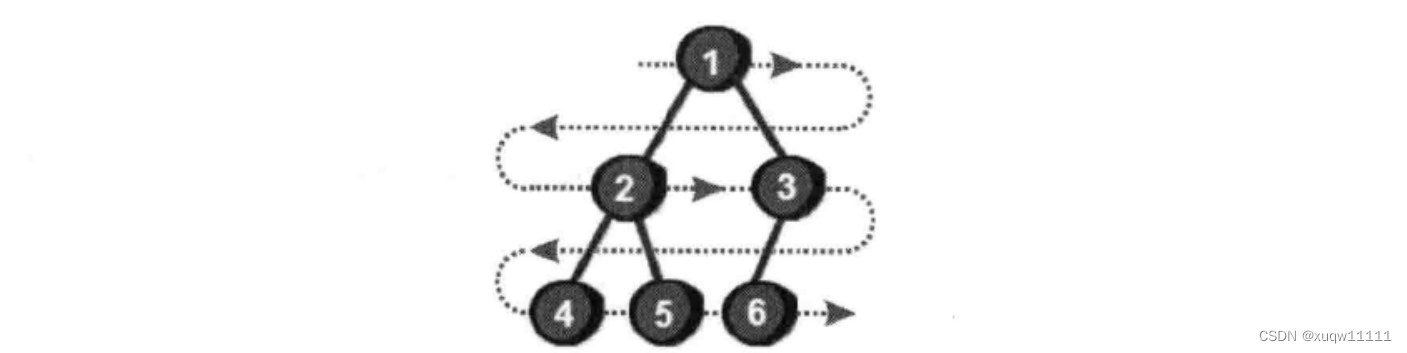
通过上图我们发现，如果完全二叉树的一个父结点编号为k，那么它左儿子的编号就是2*k，右儿子的编号就是2*k+1。如果已知儿子（左儿子或右儿子）的编号是x，那么它父结点的编号就是x/2，注意这里只取商的整数部分。在C语言中如果除号"/"两边都是整数的话，那么商也只有整数部分（即自动向下取整），即4/2和5/2都是2。另外如果一棵完全二叉树有N个结点，那么这个完全二叉树的高度为log2N（此处也是取整数解），简写为logN，即最多有logN层结点

3、堆

如上图所示，符合这样特点（所有子节点的数值都比父节点的数值要大的二叉树）的完全二叉树成为最小堆，所有子节点的数值都比父节点的数值要小的二叉树成为最大堆。

如果对于最小堆与最大堆不好理解，可以使用小顶堆和大顶堆进行描述。

最小堆与最大堆的作用

假如有14个数，分别是99、5、36、7、22、17、46、12、2、19、25、28、1和92，请找出这14个数中最小的数，请问怎么办呢？最简单的方法就是将这14个数从头到尾依次扫一遍，用一个循环就可以解决。这种方法的时间复杂度是O（14），也就是O（N）。

现在我们需要删除其中最小的数，并增加一个新数23，再次求这14个数中最小的一个数。请问该怎么办呢？只能重新扫描所有的数，才能找到新的最小的数，这个时间复杂度也是O（N）。假如现在有14次这样的操作（删除最小的数后再添加一个新数），那么整个时间复杂度就是O（14^2）即O（N^2）。那有没有更好的方法呢？堆这个特殊的结构恰好能够很好地解决这个问题。

首先我们将所有的数组成一个最小堆

删除并添加一个元素到最小堆

很显然最小的数就在堆顶，假设存储这个堆的数组叫做h的话，最小数就是h【1】。接下来，我们将堆顶部的数删除。将新增加的数23放到堆顶。显然加了新数后已经不符合最小堆的特性，我们需要将新增加的数调整到合适的位置。

比较23的两个子节点，取最小的进行交换

 按照上面的规则继续比较交换

我们刚才在对23进行调整的时候，竟然只进行了3次比较，就重新恢复了最小堆的特性。现在最小的数依然在堆顶，为2。而使用之前从头到尾扫描的方法需要14次比较，现在只需要3次就够了。现在每次删除最小的数再新增一个数，并求当前最小数的时间复杂度是O（3），这恰好是O（log14）即O（log2N），简写为O（logN）。

向下调整的代码实现

//向下维护堆
void shiftDown(int i) {
	while (true) {
		int t = i;
		if (2 * i > n) break;
		//判断左儿子
		if (h[2 * i] < h[i])  t = 2 * i;
		//判断右儿子
		if (2 * i + 1 <= n and h[i * 2 + 1] < h[t]) t = 2 * i + 1;

		if (t == i) break;
		else {
			//交换两个数
			int hh = h[i];
			h[i] = h[t];
			h[t] = hh;
		}
		//更新i的数值 
		i = t;
	}
	return;
}

新增一个数值到最小堆

如果只是想新增一个值，而不是删除最小值，又该如何操作呢？即如何在原有的堆上直接插入一个新元素呢？只需要直接将新元素插入到末尾，再根据情况判断新元素是否需要上移，直到满足堆的特性为止。如果堆的大小为N（即有N个元素），那么插入一个新元素所需要的时间为O（logN）。例如我们现在要新增一个数3.

先将3与它的父结点25比较，发现比父结点小，为了维护最小堆的特性，需要与父结点的值进行交换。交换之后发现还是要比它此时的父结点5小，因此再次与父结点交换，到此又重新满足了最小堆的特性。

向上调整的代码实现

//向上维护堆
void shiftUp(int i) {
	if (i == 1) return;
	while (i > 1 and h[i] < h[i / 2]) {
		//交换两个数
		int t = h[i];
		h[i] = h[i / 2];
		h[i / 2] = t;
		//向上推一层
		i = i / 2;
	}
	return;
}

建立一个堆

思路1：插入一个元素，进行向上维护堆一次，时间复杂度为log（n），插入n个元素时间复杂度为nlog（n）具体实现代码如下：

	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>h[i];
		shiftUp(i);
	}

思路2：先将所有的元素插入到数组堆中（堆的存储就是数组），从n/2（该堆的倒数第二行有子节点的最后一个元素）开始往上（-1）进行堆向下的维护，直到维护到堆顶为止，就建立了一个符合要求的最小堆。时间复杂度为n，具体证明使用等比数列的求和公式，具体代码如下：

	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>h[i];
	}
	for(int i=n/2;i>=1;i--){
		shiftDown(i);
	}

堆排序的基本思想

（1） 建立堆 

（2） 删除堆的顶部元素（打印输出），将最后一个元素添加到堆顶，并向下维护堆

（3） 循环执行步骤（2），直到堆中剩余一个元素。

代码实现

#include <bits/stdc++.h>
using namespace std;

int h[101];

//小顶堆的维护 加入一些保护

//向上维护堆
void shiftUp(int i) {
	if (i == 1) return;
	while (i > 1 and h[i] < h[i / 2]) {
		//交换两个数
		int t = h[i];
		h[i] = h[i / 2];
		h[i / 2] = t;
		//向上推一层
		i = i / 2;
	}
	return;
}
//向下维护堆
void shiftDown(int i, int _n) {
	while (true) {
		int t = i;
		if (2 * i > _n) break;
		//判断左儿子
		if (h[2 * i] < h[i])  t = 2 * i;
		//判断右儿子
		if (2 * i + 1 <= _n and h[i * 2 + 1] < h[t]) t = 2 * i + 1;

		if (t == i) break;
		else {
			//交换两个数
			int hh = h[i];
			h[i] = h[t];
			h[t] = hh;
		}
		//更新i的数值
		i = t;
	}
	return;
}


int main() {
	int n;
	cin >> n;
	//建立堆
	for (int i = 1; i <= n; i++) {
		cin >> h[i];
	}
	for (int i = n / 2; i >= 1; i--) {
		shiftDown(i, n);
	}
	
	//循环执行 删除堆的顶部元素（打印输出），
	//将最后一个元素添加到堆顶，并向下维护堆
	int num=n;
	for(int i=1;i<=n;i++) {
		cout << h[1] << " ";
		h[1] = h[num];
		num--;
		shiftDown(1, num);
	}
	return 0;
}

上面的排序结果只是打印输出，如果需要保存最终的结果可以重复使用h数组，使用最大堆进行排序，每次将最大值放入数组未排序元素的末尾。

代码实现

#include <bits/stdc++.h>
using namespace std;

int h[101];

//大顶堆的维护 加入一些保护
//向上维护堆
void shiftUp(int i) {
	if (i == 1) return;
	while (i > 1 and h[i] < h[i / 2]) {
		//交换两个数
		int t = h[i];
		h[i] = h[i / 2];
		h[i / 2] = t;
		//向上推一层
		i = i / 2;
	}
	return;
}
//向下维护堆
void shiftDown(int i, int _n) {
	while (true) {
		int t = i;
		if (2 * i > _n) break;
		//判断左儿子
		if (h[2 * i] > h[i])  t = 2 * i;
		//判断右儿子
		if (2 * i + 1 <= _n and h[i * 2 + 1] > h[t]) t = 2 * i + 1;

		if (t == i) break;
		else {
			//交换两个数
			int hh = h[i];
			h[i] = h[t];
			h[t] = hh;
		}
		//更新i的数值
		i = t;
	}
	return;
}


int main() {
	int n;
	cin >> n;
	//建立堆
	for (int i = 1; i <= n; i++) {
		cin >> h[i];
	}
	for (int i = n / 2; i >= 1; i--) {
		shiftDown(i, n);
	}
	
	//循环执行 删除堆的顶部元素（打印输出），
	//将最后一个元素添加到堆顶，并向下维护堆
	int num=n;
	for(int i=1;i<=n;i++) {
//		cout << h[1] << " ";
		int maxData=h[1];
		h[1] = h[num];
		h[num]=maxData;
		num--;
		shiftDown(1, num);
	}
	for(int i=1;i<=n;i++){
		cout<<h[i]<<" ";
	}
	return 0;
}

测试数据为：

14
99 5 36 7 22 17 46 12 2 19 25 28 1 92

注意事项

（1） 堆排序的时间复杂度为nlog（n）。

（2） 堆排序是一种不稳定的排序方式。