本节介绍行列式性质的几何意义,也就是行列式的性质与有序单形的体积的性质之间的关系。
0 关于有序单形以及其与行列式的关系请点这里
1根据有序单形体积的性质推断出行列式的性质,该方法最早由阿根廷人提出。
D表示以a1,a2,...,an为列的矩阵的行列式
(1)性质一:若存在i不等于j有ai = aj 则行列式D = 0;
对应到有序单形,当有两个顶点重合时改单形是退化的有序单形,体积为0.
以三维空间中的有序单形为例,当两个顶点重合的时候,该单形退化为一个三角形,体积为0;
(2) 性质二:D(a1,...,an)是其自变量的多重线性函数,即如果固定全体ai(i不等于j)则D是自变量aj的线性函数。
当其他顶点固定时候单形的体积等于aj到其他顶点所在超平面的高度h乘超平面的体积S,而S是固定的.并且h是
aj的线性函数(由于aj与h的夹角是固定的,想想三维空间中一个向量的的端点到一个平面的距离)
(3) 性质三:标准化: D(e1,...,en) = 1.
这条性质很好理解,此时单形的边互相垂直,以三维空间为例此时的单形的体积是1/(3!)
D的其他性质都可以从以上三条性质推出
(4)性质四:如果交换D的自变量ai和aj,D的值将改变一个因子(-1 也就是d的符号会改变)
对应于有序单形,如果交换两个顶点的位置,那么顶点会到其超平面的另一侧,因此单形体积的符号会改变
下边利用性质(1)和性质(2)给出证明:
(5)若a1,a2,...,an线性相关,则D(a1,...an) = 0;
当向量线性相关的时候说明对应的单形是退化的单形,
以三维空间为例 此时的三个向量是共面的,因此体积是0;
下边利用性质(1)和性质(2)给出证明:
因为a1,..,an线性相关,假设a1 = k2a2+k3a3+,...,+knan;则:








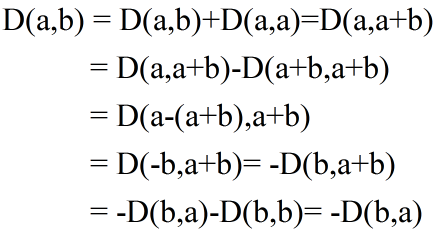















 3334
3334











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








