本节将实数域上的完备性与局部紧致性推广到欧几里得空间上的向量上.
0 首先回忆几个概念:
(i) 收敛
设{ak}为一数列,如果:
则称{ak}收敛于a,记做:
(ii)柯西列
柯西列是满足:
的序列
下边是柯西列与非柯西列的示例:
(iii)完备性
实数的一个基本性质就是柯西列均收敛,这一性质叫做实数的完备性.
完备性指的是实数域上的所有柯西列都收敛于一个实数.
完备性用直观的话说就是实数的数轴是没有洞的.就是说任何地方都存在数.
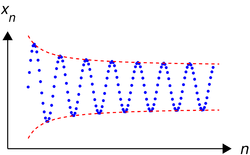
有理数就不是完备的.因为有理数上的某些柯西列收敛于无理数.如:
(iv)局部紧致性
实数域内任何有界序列都包含收敛子列.
局部紧致性是比完备性更强的性质.说的是一个有界的实数列由于数列中的数是无线的.
而这些点又没有洞来逃逸.所以极限点一定存在.
1 向量的收敛性
设{x1,x2,..,xk}是欧几里得空间X中的一列向量.如果当:
则称该数列收敛于x或以x为极限.记做:
2 向量的完备性与局部紧致性
如果欧几里得空间X中的向量列{xk}满足:
则称为柯西列.
(i)有限维欧几里得空间中的柯西列都有极限.
证明:
设:
则:
上式表明如果向量是柯西列那么每一个分量组成的序列也是柯西列.则有:
因此证明了:
(ii)设{xk}是欧几里得空间里的一列向量,如果存在实数R.使得对任意k都有:
则称{xk}有界.
(iii)有限维欧几里得空间中的任意有界向量列都包含于收敛子列.
证明:
由于:
因此每个分量组成的序列是有界的.根据局部紧致性.存在:
我们可以构造由每个分量的极限组成的:
我们构造的子列就收敛于上边的x.
3 有限维空间的判断
设X是具有欧几里得结构并且局部紧致的线性空间.即X中向量的任意有界序列{xk}都有收敛子列.则x是有限维空间
证明(简略):
考虑无线维空间的标准正交基序列{xk}:
此序列显然有界但是却不收敛.任意连个向量的距离的平方不会小于2.因此不具备局部紧致性.
4 映射的收敛性
如果一列映射{A1,A2,...,An}满足:
则称{An}收敛于A或以A为极限.








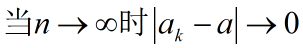
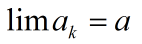
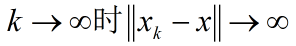
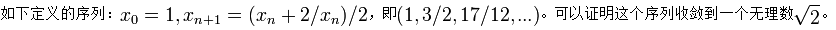
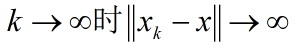
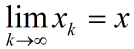
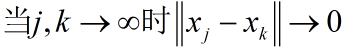
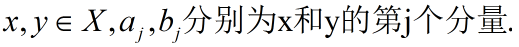
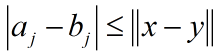
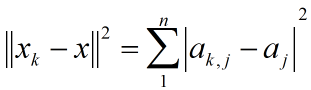
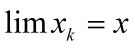
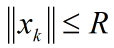
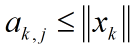
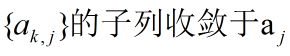
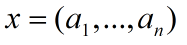
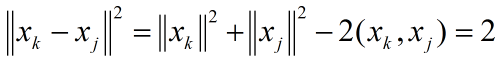
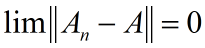














 4436
4436

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








