朴素贝叶斯(naïve Bayes)分类器是一种常用的分类算法,属于机器学习十大算法之一。正如其名称所体现的,朴素贝叶斯分类器的确很“朴素”,可以说它是贝叶斯理论甚至分类算法中最简单的算法之一。先看一看贝叶斯定理——
贝叶斯定理
贝叶斯定理如下:
其中P(A|B)是表示B发生的情况下A发生的概率。这个定理有什么用呢?
我们先来看一个例子:春节到了,老妈包了300个饺子(假设这300个饺子外形都一样),其中有100个猪肉馅的,150个羊肉馅的,50个韭菜馅的,那么我们很容易知道,吃一个饺子吃到羊肉馅的概率是1/2。假如我并不知道每种馅的饺子各有多少,而是根据已经吃掉的饺子中各种馅的比例来预测我下一个吃到羊肉馅饺子的概率,这就是贝叶斯定理的思想。
现实生活中,我们有很多时候并不能知道事件发生的准确概率,只能通过统计已发生的情况来预测未发生情况的概率,可以称这种概率为“逆概率”,贝叶斯定理正是用来解决“逆概率”问题日常生活中,像天气预报、彩票中奖预测等,都有这种思想的存在。我们来看上面的定理:
我们已知A和B事件发生的概率以及在A发生的情况下B发生的概率,那么通过这些已知条件便能通过上面的公式求出B发生的条件下A发生的概率。这里我们需要知道几个概念:
- 先验概率:现在我们知道A、B的概率及A条件下B发生的概率,即P(A)、P(B)、P(B|A),P(A)就是先验概率,就是我们对事件A的一个主观判断,一般是通过经验可知的;
- 后验概率:P(A|B)称为“后验概率”,就是事件B发生后,对事件A发生的可能性进行了重新评估。
对于这两个概念,我觉得这篇文章分析的很透彻,链接附上:https://www.jianshu.com/p/4d5e3655269e
朴素贝叶斯
我们假设类别为c={c1,c2,…,cd},样本集为X={(x1,y1),…,(xm,ym)},每个分量xi={xi1,…,xid}则根据贝叶斯定理,有:
根据全概率公式,我们可以得到:
我们假设在类别已知的情况下,样本的每个属性值间相互独立,各个样本之间也相互独立,则可得出:
这就是朴素贝叶斯分类器。
极大似然估计
根据上面的式子,可以看出在朴素贝叶斯分类中,就是学习P(ck)和P(xi|ck)的值。我们可以通过极大似然估计得到相应的概率。首先,P(ck)的极大似然估计为:
其中I(yi=ck)为指示函数,yi=ck时为1,不等时为0;设第i个特征xi可能的取值集合为{ai1,ai2,…,aim},则P(xi|ck)的极大似然估计为:
朴素贝叶斯的一些问题
下溢问题
数值下溢问题是指计算机浮点数计算的结果小于可以表示的最小数,因为计算机的能力有限,当数值小于一定数时,其无法精确保存,会造成数值的精度丢失,由上述公式可以看到,求概率时多个概率值相乘,得到的结果往往非常小;因此通常采用取对数的方式,将连乘转化为连加,以避免数值下溢。
零概率问题
零概率问题,就是在计算实例的概率时,如果某个量x,在观察样本库(训练集)中没有出现过,会导致整个实例的概率结果是0。
在实际的模型训练过程中,可能会出现零概率问题(因为先验概率和反条件概率是根据训练样本算的,但训练样本数量不是无限的,所以可能出现有的情况在实际中存在,但在训练样本中没有,导致为0的概率值,影响后面后验概率的计算),即便可以继续增加训练数据量,但对于有些问题来说,数据怎么增多也是不够的。这时我们说模型是不平滑的,我们要使之平滑,一种方法就是将训练(学习)的方法换成贝叶斯估计。
Python实现
import numpy as np
import math
# naive Bayes
class NaiveBayes:
def __init__(self):
self.model = None
# 数学期望
@staticmethod
def mean(X):
"""计算均值
Param: X : list or np.ndarray
Return:
avg : float
"""
avg = 0.0
# ========= show me your code ==================
avg = np.mean(X)
# ========= show me your code ==================
return avg
# 标准差(方差)
def stdev(self, X):
"""计算标准差
Param: X : list or np.ndarray
Return:
res : float
"""
res = 0.0
# ========= show me your code ==================
# here
res = math.sqrt(np.mean(np.square(X-self.mean(X))))
# ========= show me your code ==================
return res
# 概率密度函数
def gaussian_probability(self, x, mean, stdev):
"""根据均值和标注差计算x符号该高斯分布的概率
Parameters:
----------
x : 输入
mean : 均值
stdev : 标准差
Return:
res : float, x符合的概率值
"""
res = 0.0
# ========= show me your code ==================
# here
exp = math.exp(-math.pow(x - mean, 2) / 2 * math.pow(stdev, 2))
res = (1 / (math.sqrt(2 * math.pi) * stdev)) * exp
# ========= show me your code ==================
return res
# 处理X_train
def summarize(self, train_data):
"""计算每个类目下对应数据的均值和标准差
Param: train_data : list
Return : [mean, stdev]
"""
summaries = [0.0, 0.0]
# ========= show me your code ==================
# here
summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
# ========= show me your code ==================
return summaries
# 分类别求出数学期望和标准差
def fit(self, X, y):
labels = list(set(y))
data = {label: [] for label in labels}
for f, label in zip(X, y):
data[label].append(f)
self.model = {
label: self.summarize(value) for label, value in data.items()
}
return 'gaussianNB train done!'
# 计算概率
def calculate_probabilities(self, input_data):
"""计算数据在各个高斯分布下的概率
Paramter:
input_data : 输入数据
Return:
probabilities : {label : p}
"""
# summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)], 1.0: [(5.8, 0.449),(2.7, 0.27)]}
# input_data:[1.1, 2.2]
probabilities = {}
# ========= show me your code ==================
for label, value in self.model.items():
probabilities[label] = 1
# here
for i in range(len(value)):
mean, stdev = value[i]
probabilities[label] *= self.gaussian_probability(input_data[i], mean, stdev)
# ========= show me your code ==================
return probabilities
# 类别
def predict(self, X_test):
# {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
label = sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
return label
# 计算得分
def score(self, X_test, y_test):
right = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right += 1
return right / float(len(X_test))
参考资料
- (转)贝叶斯的理解https://www.jianshu.com/p/4d5e3655269e
- 贝叶斯统计https://zhuanlan.zhihu.com/p/38553838
- 深入理解朴素贝叶斯(Naive Bayes)https://blog.csdn.net/li8zi8fa/article/details/76176597
- 朴素贝叶斯分类模型(一)https://blog.csdn.net/u013850277/article/details/83996358
- 《统计学习方法》.李航
- 《机器学习》.周志华










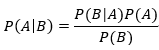
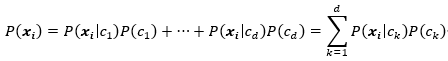
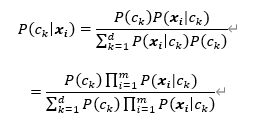
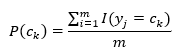
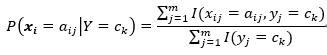














 438
438











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








