基于离散时间系统的SIR模型-CSDN博客

本文链接：https://blog.csdn.net/xyhxx99499/article/details/148040901

在疫情防控的关键时期，如何准确预测传染病的传播趋势成为了全球关注的焦点。数学模型作为一种强大的工具，可以帮助我们理解疾病传播的机制，并为公共卫生决策提供科学依据。今天，我们将深入探讨一个基于随机微分方程的传染病传播模型，通过 MATLAB 代码实现并可视化分析，揭示传染病传播的内在规律。

一、SIR 模型：传染病传播的基础框架

SIR 模型是传染病动力学中最经典的模型之一，它将人群分为三类：

易感者 (Susceptible)：尚未感染但可能被感染的个体
感染者 (Infected)：已经感染并具有传染性的个体
康复者 (Recovered)：已经康复并获得免疫力的个体

模型通过两个关键参数描述疾病传播过程：

β(beta)：传染率，表示接触导致感染的概率
γ(gamma)：恢复率，表示感染者康复的速率

在这个模型中，我们还引入了一个新参数：

ι(iota)：外部输入率，表示外部感染源的影响

下面是 SIR 模型的核心代码实现：

function [S_next, I_next, R_next, Y_next] = sir(S, I, R, Y, parms)
    % 解包参数
    beta  = parms.beta;
    gamma = parms.gamma;
    iota  = parms.iota;
    N     = parms.N;
    dt    = parms.dt;
    
    % 计算感染力和二项式概率
    lambda = beta * (I + iota) / N;
    ifrac  = 1 - exp(-lambda * dt);
    rfrac  = 1 - exp(-gamma * dt);
    
    % 随机抽取转换人数
    infection = binornd(S, ifrac);
    recovery  = binornd(I, rfrac);
    
    % 更新各类人群数量
    S_next = S - infection;
    I_next = I + infection - recovery;
    R_next = R + recovery;
    Y_next = Y + infection;
end

这段代码实现了 SIR 模型的核心逻辑：

计算感染力 λ，表示单位时间内易感者接触到感染者的概率
利用指数函数将连续时间的参数转换为离散时间步长 dt 内的概率
使用二项分布随机抽样，模拟感染和康复过程的随机性
更新各类人群的数量，并记录累计感染人数

二、随机模拟：捕捉传染病传播的不确定性

在现实世界中，传染病的传播具有很大的随机性。例如，一次偶然的大规模聚集可能导致感染人数激增，而严格的防控措施又可能迅速遏制疫情。为了捕捉这种不确定性，我们使用随机微分方程进行模拟。

下面是模拟代码：

% Parameters: [beta, gamma, iota, N, dt]
parms = struct( ...
    'beta',  0.1, ...
    'gamma', 0.05, ...
    'iota',  0.01, ...
    'N',     1000, ...
    'dt',    0.1  ...
);
tf = 200;  % 模拟总时间
tl = 2001; % 时间点数量
t  = linspace(0, tf, tl); % 生成时间向量

% 预分配内存
S = zeros(1, tl);
I = zeros(1, tl);
R = zeros(1, tl);
Y = zeros(1, tl);  % 累计新感染人数

% 初始状态
S(1) = 999;  % 初始易感者
I(1) =   1;  % 初始感染者
R(1) =   0;  % 初始康复者
Y(1) =   0;  % 初始累计感染人数

% 时间步进循环
for j = 2:tl
    [S(j), I(j), R(j), Y(j)] = sir( ...
        S(j-1), I(j-1), R(j-1), Y(j-1), parms);
end

% 将结果存入结构体
results.t = t;
results.S = S;
results.I = I;
results.R = R;
results.Y = Y;

这段代码完成了整个模拟过程：

定义模型参数，包括传染率、恢复率、外部输入率等
设置模拟时间范围和时间步长
初始化各类人群的数量
通过时间步进循环，逐点计算每个时间点的人群数量
将结果存储在结构体中，便于后续分析和可视化

三、结果可视化：直观展示传染病传播动态

可视化是理解模型结果的关键步骤。通过绘制不同人群随时间的变化曲线，我们可以直观地观察传染病的传播趋势。

下面是可视化代码：

% 假设已经完成模拟：res = simulate();

figure;
hold on;

% 绘制各类人群随时间的变化
plot(res.time, res.S, 'r', 'LineWidth', 2);  % 易感者 - 红色
plot(res.time, res.I, 'g', 'LineWidth', 2);  % 感染者 - 绿色
plot(res.time, res.R, 'b', 'LineWidth', 2);  % 康复者 - 蓝色

% 添加标签和图例
xlabel('Time', 'FontWeight', 'bold');
ylabel('Number', 'FontWeight', 'bold');
legend('Susceptible','Infected','Recovered', 'Location','best');

hold off;

运行这段代码后，我们将得到一个包含三条曲线的图表：

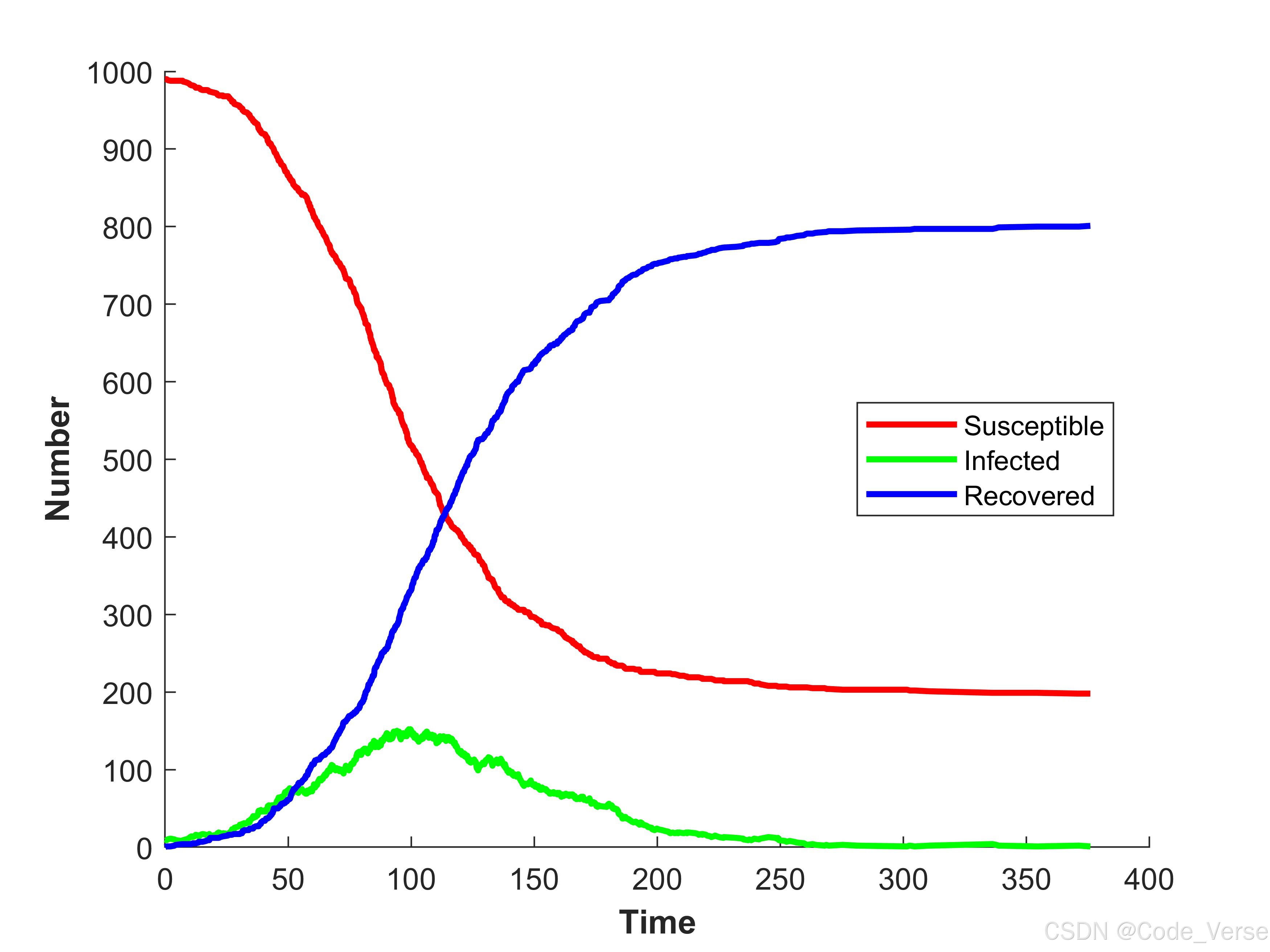
红色曲线：表示易感者数量随时间的变化。随着感染的传播，易感者数量逐渐减少。
绿色曲线：表示感染者数量随时间的变化。通常会呈现先上升后下降的钟形曲线，反映疫情的爆发和消退过程。
蓝色曲线：表示康复者数量随时间的变化。随着感染者康复，康复者数量持续增加。

四、模型分析：解读传染病传播的关键指标

通过分析模拟结果，我们可以获得以下关键指标：

1. 基本再生数 R₀

基本再生数 R₀是传染病传播的重要指标，定义为一个感染者在易感人群中能够平均感染的人数。在 SIR 模型中，R₀可以近似计算为： \(R_0 = \frac{\beta}{\gamma}\) 当 R₀ > 1 时，疫情会爆发；当 R₀ < 1 时，疫情会逐渐消退。在我们的模型中，R₀ = 0.1/0.05 = 2，表示一个感染者平均能感染 2 个人，疫情会迅速传播。