数据降维利器：主成分分析 (PCA) 的数学原理与 MATLAB 实现

最新推荐文章于 2025-05-21 08:29:48 发布

Code_Verse

最新推荐文章于 2025-05-21 08:29:48 发布

阅读量939

点赞数 17

文章标签： matlab 数学建模

本文链接：https://blog.csdn.net/xyhxx99499/article/details/148045517

版权

#新星杯·14天创作挑战营·第11期#

在大数据时代，我们常常面临高维数据的挑战：变量过多不仅增加计算复杂度，还可能引入噪声干扰分析结果。主成分分析 (Principal Component Analysis, PCA) 作为一种强大的数据降维技术，能够在保留数据主要特征的前提下，将高维数据映射到低维空间。今天，我们就通过一段 MATLAB 代码，深入探索 PCA 的数学原理、实现过程与应用场景。

一、PCA 核心思想：用更少的维度捕捉更多的信息 🎯

PCA 的核心目标是找到一组新的正交变量（主成分），这些主成分按方差递减排序，并且能够解释原始数据的大部分变异。简单来说：

降维：将高维数据转换为低维表示
信息浓缩：用少数几个主成分保留原始数据的主要信息
噪声过滤：去除数据中的次要波动，突出主要特征

例如，在人脸识别中，PCA 可以将数千个像素点压缩为几十个特征向量，同时保留面部的关键特征。

二、PCA 数学原理：从协方差矩阵到特征分解 🧮

1. 数据标准化

PCA 对数据尺度敏感，因此通常需要先对数据进行标准化处理： \(x_{\text{standard}} = \frac{x - \mu}{\sigma}\) 其中，\(\mu\)是均值，\(\sigma\)是标准差。标准化后的数据均值为 0，方差为 1。

% 数据标准化代码
x_mean = mean(x);
x_std = std(x);
x_stadard = (x - x_mean) ./ x_std;

2. 计算相关系数矩阵

相关系数矩阵衡量了变量间的线性相关性，是 PCA 的基础： \(R = \text{corrcoef}(x_{\text{standard}})\) 相关系数矩阵是对称正定矩阵，其对角线元素为 1（变量与自身的相关系数）。

3. 特征分解：寻找主成分

对相关系数矩阵进行特征分解： \(R = VDV^T\) 其中：

V是特征向量矩阵，每列代表一个主成分方向
D是对角矩阵，对角线元素为特征值，对应主成分的方差

% 特征分解代码
R = corrcoef(x_stadard);
[V, D] = eig(R);

4. 主成分排序与贡献度计算

特征值按降序排列后，计算每个主成分的贡献率和累积贡献率： \(\text{贡献率} = \frac{\lambda_i}{\sum_{j=1}^p \lambda_j}\) \(\text{累积贡献率} = \sum_{i=1}^k \frac{\lambda_i}{\sum_{j=1}^p \lambda_j}\)

% 特征值排序与贡献度计算
lambda = diag(D);
lambda = lambda(end: -1: 1);  % 降序排列
contribution = lambda ./ sum(lambda);  % 贡献率
accu_contribution = cumsum(contribution);  % 累积贡献率

三、PCA 实现步骤详解：从代码到可视化 🕹️

1. 数据准备与标准化

首先对原始数据进行中心化和标准化，消除量纲影响。这一步很关键，因为 PCA 本质上是通过方差最大化来确定主成分方向。

2. 计算相关系数矩阵

相关系数矩阵反映了变量间的线性关系强度。例如，在金融数据分析中，两个股票收益率的相关系数接近 1，表示它们具有很强的同向变动关系。

3. 特征分解与主成分提取

特征分解是 PCA 的核心步骤。特征向量方向决定了主成分的方向，特征值大小表示该主成分解释的方差量。通常保留累积贡献率超过 80% 的前 k 个主成分。

4. 结果可视化：碎石图与贡献度分析

碎石图 (Scree Plot) 是展示特征值与主成分关系的常用工具：

% 绘制碎石图示例
figure;
subplot(2,1,1);
plot(1:length(lambda), lambda, 'o-', 'LineWidth', 2);
xlabel('主成分序号'); ylabel('特征值');
title('特征值分布（碎石图）');
grid on;

subplot(2,1,2);
plot(1:length(lambda), accu_contribution, 'o-', 'LineWidth', 2);
hold on;
plot([0 length(lambda)], [0.8 0.8], 'r--', 'LineWidth', 1);
xlabel('主成分数量'); ylabel('累积贡献率');
title('主成分累积贡献率');
legend('累积贡献率', '80%阈值');
grid on;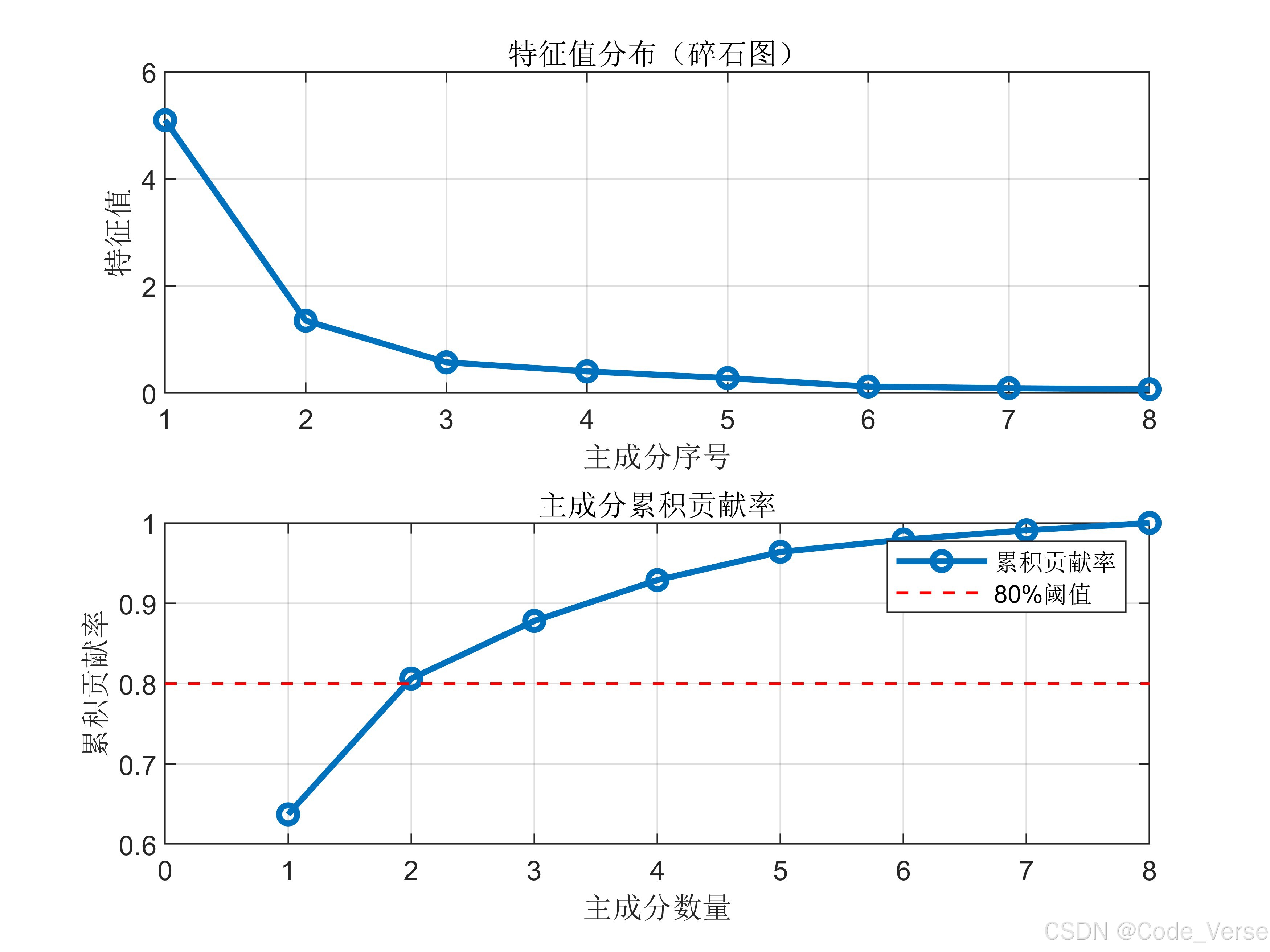

碎石图中，特征值快速下降后趋于平缓的转折点，通常是选择主成分数量的参考点。

四、PCA 应用场景：从数据压缩到特征提取 🚀

1. 数据可视化

将高维数据降维到 2D 或 3D 空间，便于直观理解数据分布。例如，在基因表达数据分析中，PCA 可以将数千个基因表达值映射到二维平面，发现样本间的聚类关系。

2. 特征提取

在机器学习中，PCA 常被用于特征提取，减少模型复杂度。例如，在图像识别中，PCA 可以提取图像的主要特征，降低计算量的同时提高识别准确率。

3. 噪声过滤

PCA 具有一定的噪声过滤能力。由于噪声通常表现为方差较小的成分，通过保留主要主成分，可以有效去除噪声。

4. 多重共线性处理

在回归分析中，变量间的多重共线性会影响模型稳定性。PCA 通过生成正交的主成分，消除了共线性问题。

五、PCA 的优缺点与注意事项 ⚖️

1. 优点

无监督学习：无需标签信息，仅基于数据自身方差结构
计算高效：特征分解算法成熟，计算速度快
解释性强：主成分按方差贡献排序，便于理解数据结构

2. 缺点

线性假设：只能捕捉线性关系，对非线性结构无能为力
可解释性下降：主成分通常是原始变量的复杂组合，难以直观解释
异常值敏感：标准化过程可能放大异常值的影响

3. 注意事项

数据标准化：必须进行标准化处理，除非变量量纲相同
主成分选择：根据累积贡献率或碎石图确定主成分数量
结果解释：主成分方向可能与原始变量方向不同，需谨慎解释

六、PCA 拓展：核 PCA 与增量 PCA 🌟

1. 核 PCA (Kernel PCA)

核 PCA 通过核函数将数据映射到高维特征空间，再进行 PCA，能够处理非线性降维问题。例如，在人脸识别中，核 PCA 可以更好地捕捉面部的非线性特征。

2. 增量 PCA (Incremental PCA)

对于大规模数据集，传统 PCA 计算开销大。增量 PCA 通过分批次处理数据，逐步更新主成分，适用于在线学习场景。

结语：PCA—— 数据科学工具箱中的瑞士军刀 🛠️

主成分分析作为数据降维的经典方法，在数据分析、机器学习、信号处理等领域有着广泛应用。通过特征分解，PCA 帮助我们从高维数据中提取关键信息，发现数据背后的潜在结构。无论是探索性数据分析，还是作为机器学习的预处理步骤，PCA 都是值得信赖的工具。

下次面对高维数据时，不妨试试 PCA，让数据的主要特征 “一目了然”～ 🌟

互动话题：你在实际项目中是如何应用 PCA 的？遇到过哪些挑战？欢迎在评论区分享你的经验！👇

完整代码（省流版）

x_mean = mean(x);
x_std = std(x);
x_stadard = (x - x_mean) ./ x_std;
R = corrcoef(x_stadard);
[V, D] = eig(R);
lambda = diag(D);
lambda = lambda(end: -1: 1);
contribution = lambda ./ sum(lambda);
accu_contribution = cumsum(contribution);
% 绘制碎石图示例
figure;
subplot(2,1,1);
plot(1:length(lambda), lambda, 'o-', 'LineWidth', 2);
xlabel('主成分序号'); ylabel('特征值');
title('特征值分布（碎石图）');
grid on;

subplot(2,1,2);
plot(1:length(lambda), accu_contribution, 'o-', 'LineWidth', 2);
hold on;
plot([0 length(lambda)], [0.8 0.8], 'r--', 'LineWidth', 1);
xlabel('主成分数量'); ylabel('累积贡献率');
title('主成分累积贡献率');
legend('累积贡献率', '80%阈值');
grid on;