基于FreeFEM++的有限元编程--3

目录

前言

1、泊松方程的描述

2、结果保存和读取

3、更多网格生成方法

4、边界条件介绍

5、总结，

---

前言

FreeFem++是通过有限元方法求解PDE的免费软件，该软件由法国第六大学开发，可以运行在windows、linux和Mac系统上。可以进行网格生成、自动建立有限元模型、整合了各类线性求解器、能适用于与二维和三维问题，可以生成图片、文字和文件作为计算结果的输出。使用方法是编写脚本文件、保存为后缀为.edp为后缀的文本文件，运行软件调用该脚本文件即可。

用网上找到的材料，通过六类方程学习如何用FreeFem进行有限元模拟，这几个例子分别设计泊松方程、弹性方程、斯托克斯方程（Stokes）、纳维-斯托克斯方程（Navier-Stokes equations，NS方程）、耦合系统、向量到网格。由于长度问题，这篇先写第一类问题，泊松方程问题。

1、泊松方程的描述

利用FreeFem++进行包括5个步骤，定义网格、定义问题、求解、保存。

定义一个在固定边界（Dirichlet）上的泊松方程，下面展示了泊松方程的原始形式、变分形式和格林估计形式（采用P1形式的有限元，即三角形的边用两个点的线段表示）。

 

bool debug=true;

mesh Sh = square(10,10);   //mesh generation of a square

plot(Sh, wait=debug);    //Plot the initial mesh

fespace Vh(Sh, P1);  // space of P1 Finite Elements

Vh u, v;   // u and v belongs to Vh

func f=cos(x)*y;  // f is a function of x and y

problem Possion(u,v)=    // Definition of the problem

    int2d(Sh)(dx(u)*dx(v)+dy(u)*dy(v))    // bilinear form

    -int2d(Sh)(f*v)          // linear form

+on(1,2,3,4,u=0);            // Dirichlet Conditions

Possion;              // Solve Poisson Equation

plot(u);       // Plot the result

 

 

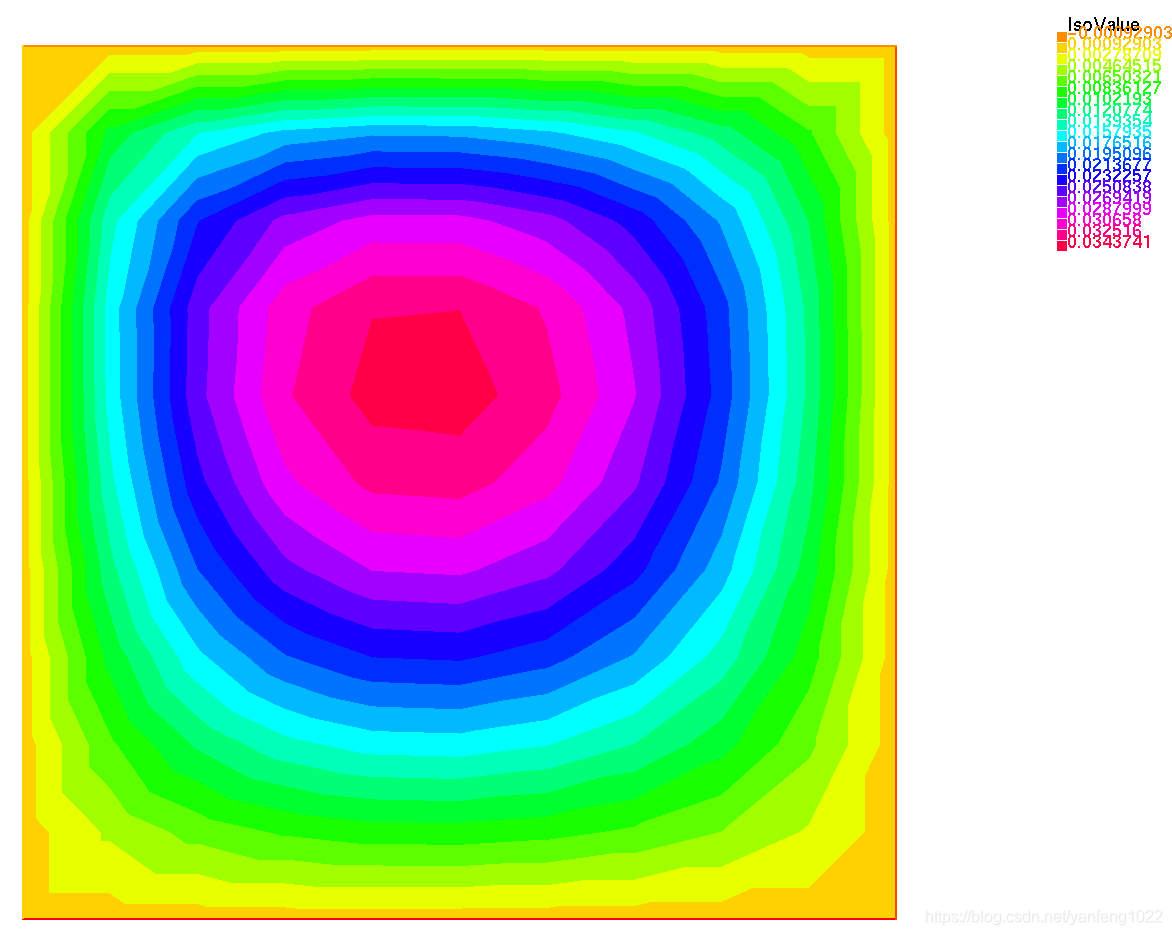
2、结果保存和读取

保存网格和结果

include "possion1.edp";        // include previous script

plot(u, ps="result.eps");     // Generate eps output

savemesh(Sh,"Sh.msh");         // Save the Mesh

ofstream file("potential.txt");

file<<u[];

 

读取网格和结果

mesh Sh=readmesh("Sh.msh"); // Read the Mesh

fespace Vh(Sh,P1);

Vh u=0;

ifstream file("potential.txt");

file>>u[]; // Read the potential

plot(u,cmm="The result was correctly saved :)");

 

3、更多网格生成方法

关键词square只能生成结构化网格，更通用的网格可以通过关键词border和buldmesh生成，它可以用一组参数化的曲线表示网格的边界。比如下面的例子：

 

border a(t=0,2.*pi){x=cos(t);y=sin(t);};

mesh Sh1=buildmesh(a(20));

plot(Sh1, wait=true, cmm="The unit dist");

 

border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)*0.2+0.3;};

mesh Sh2=buildmesh(a(20)+b(-20));

plot(Sh2,wait=true,cmm="The unit disk with a hole");

 

mesh Sh3=buildmesh(a(20)+b(20));

plot(Sh3,wait=true,cmm="The unit disk with an inclusion");

 

 

 

 

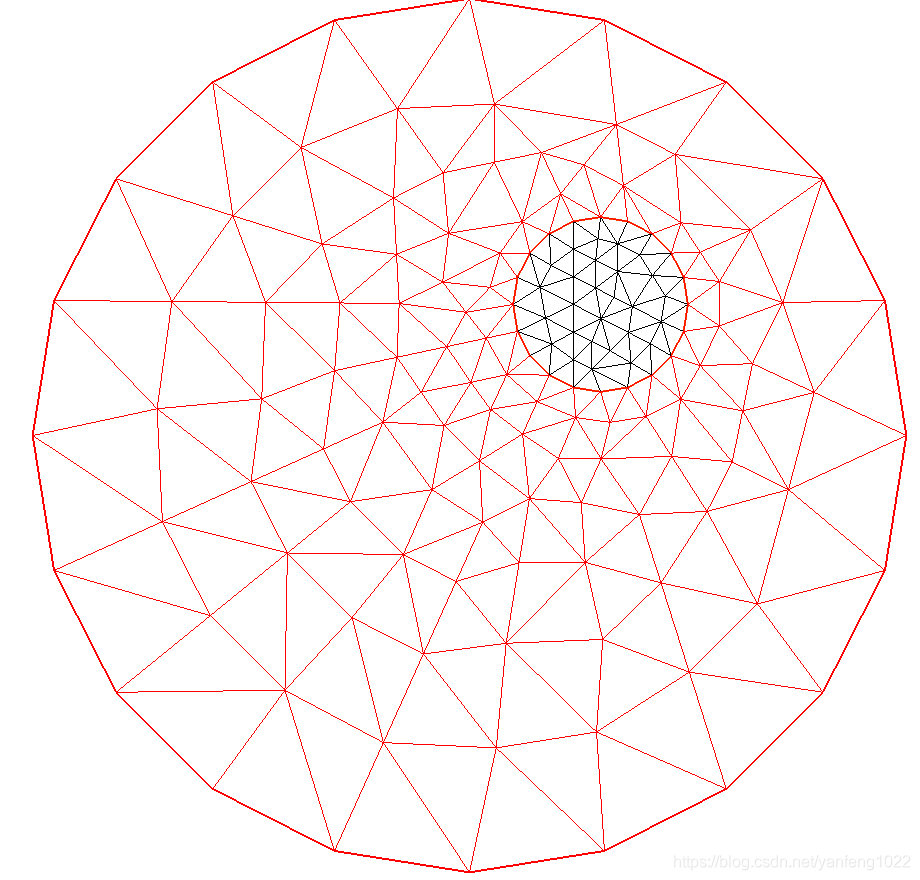
下面是定义在带洞圆饼上的泊松方程

int Dirichlet=1;    // For label definition

border a(t=0,2.*pi){x=cos(t);y=sin(t); 

    label=Dirichlet;};

border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=0.2*sin(t)+0.3; 

    label=Dirichlet;};

mesh Sh=buildmesh(a(80)+b(-20));  // The Unit Disk with a hole

plot(Sh, wait=true);

fespace Vh(Sh, P1);

Vh u,v;

func f=cos(x)*y;

problem Possion(u,v)=    // Definition of the problem

    int2d(Sh)(dx(u)*dx(v)+dy(u)*dy(v))    // bilinear form

    -int2d(Sh)(f*v)          // linear form

+on(Dirichlet,u=0);            // Dirichlet Conditions

Possion;              // Solve Poisson Equation

plot(u);       // Plot the result

 

 

 

 

 

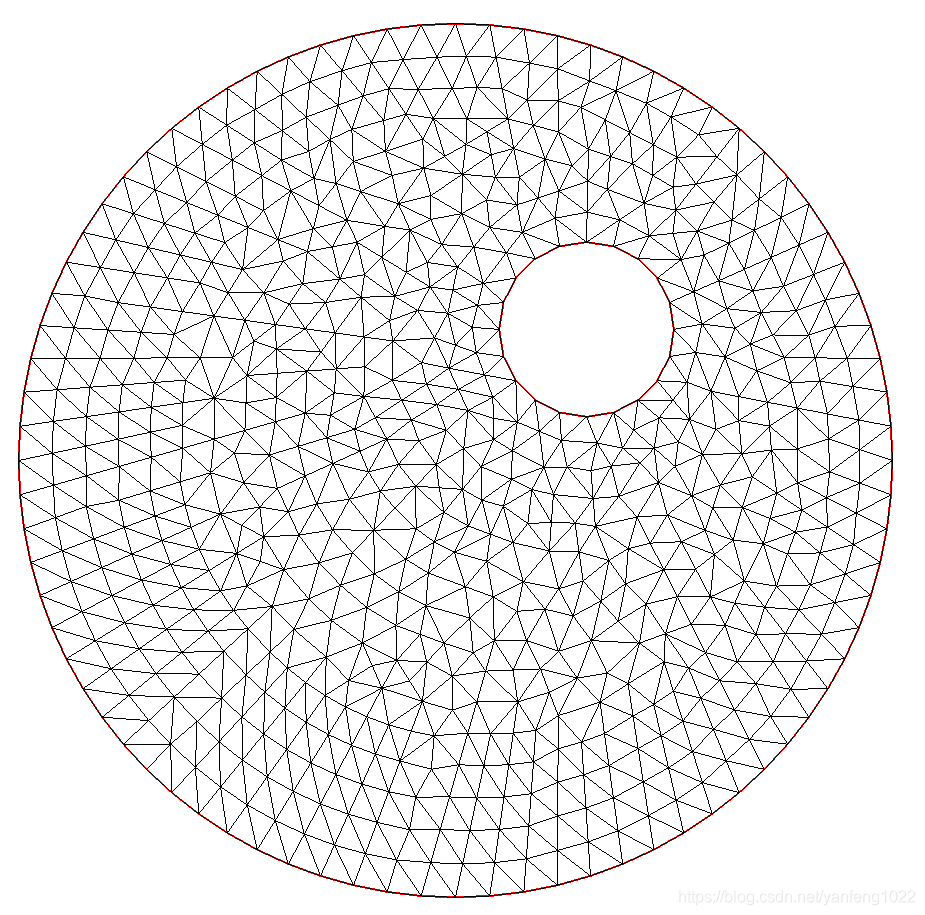
4、边界条件介绍

实际的工程问题都是有限边界，而不是无线边界。常见的边界条件有狄利克雷（Dirichlet）边界条件、诺伊曼Neumann边界条件、柯西边界条件和混合边界条件等。

在数学中，狄利克雷边界条件，为常微分方程的“第一类边界条件”，以彼得·古斯塔夫·狄利克雷（1805-1859）命名。当对一个常微分方程或偏微分方程施加时，它指定了微分方程的解在边界处的值。求出这样的方程的解的问题被称为狄利克雷问题。在应用科学中，狄利克雷边界条件也可以称为固定边界条件

第二类边界条件即诺依曼边界条件（Neumann boundary condition），给出了在边界处解对指定函数的导数或偏导数。例如，泊松方程中的浮动边界条件，电势可以浮动，电场（负的电势梯度）为零。

柯西边界条件是强加在常微分方程或偏微分方程的边界条件，而边界条件则是其方程的解都要符合在边界的给定条件。一组柯西边界条件通常包含在边界的函数值及导数，这相当于给定狄利克雷边界条件和诺伊曼边界条件。柯西边界条件的名字是纪念19世纪的著名数学家-柯西。

混合边界条件是狄利克雷边界条件和诺依曼边界条件的和混合，比如有四个边界，两个边界满足狄利克雷边界条件而另外两个边界满足诺依曼边界条件。

下面的例子展示了混合限边界条件下三种方程的关系：

 

int Dirchlet=1, Neumann=2;        // For label definition

border a(t=0, 2.*pi){x=cos(t);y=sin(t); label=Dirchlet;};

border b(t=0, 2.*pi){x=0.2*cos(t)+0.3;y=0.2*sin(t)+0.3;label=Neumann;};

mesh Sh = buildmesh(a(80)+b(-20));

plot(Sh, wait=true);

fespace Vh(Sh, P1);

Vh u, v;

func f=cos(x)*y;

func ud=x;

func g=1;

problem Possion(u,v)=

    int2d(Sh)(dx(u)*dx(v)+dy(u)*dy(v))

    +int1d(Sh, Neumann)(g*v)

    -int2d(Sh)(f*v)

+on(Dirchlet, u=ud);         // u=ud on label=Dirichlet=1

Possion;

plot(u);

 

 

 

 

 

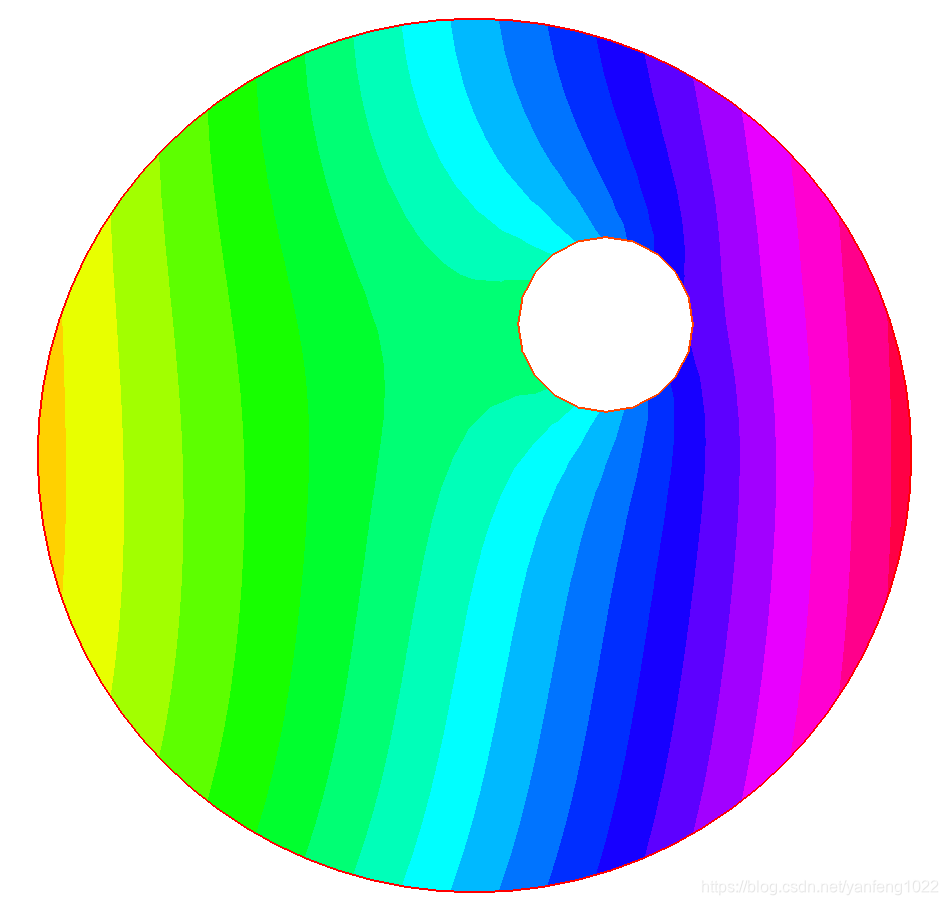
针对上述问题，可以采用自适应网格adapmesh的方法求解，可以看出网格变化之后计算结果也发生了较大的变化：

 

int Dirichlet=1,Neumann=2;

border a(t=0,2.*pi){x=cos(t);y=sin(t);label=Dirichlet;};

border b(t=0,2.*pi){x=0.2*cos(t)+0.3;y=sin(t)*0.2+0.3;label=Neumann;};

mesh Sh=buildmesh(a(80)+b(-20));

plot(Sh, wait=true);

fespace Vh(Sh,P1); Vh u,v;

func f=cos(x)*y; func ud=x; func g=1.;

problem Poisson(u,v)=

    int2d(Sh)(dx(u)*dx(v)+dy(u)*dy(v))

    -int1d(Sh,Neumann)(g*v)-int2d(Sh)(f*v)

+on(Dirichlet,u=ud);

Poisson;

plot(Sh,cmm="Initial Mesh",wait=1);plot(u,wait=1);

Sh=adaptmesh(Sh,u,err=1.e-3);

Poisson;

plot(Sh,cmm="Adapted Mesh",wait=1);plot(u);

 

 

 

 

 

5、总结，

通过这些例子学习到如下知识：

（1）关于网格

mesh 用于表示各种类型的网格

square 用于创建结构化网格

savemesh 用于保存网格到文件

reeamesh 用从文件中读取网格

border 用于表示参数化曲线

buildmesh 用于有参数化曲线定义的网格

adaptmesh 用于重新定义网格

 

（2）关于变分形式

fespace 用于表示有限元空间

problem 用于表示变分问题

P1，P2，P3 表示拉格朗日单元

int2d 表示给定域上的积分

int1d 表示部分边界上的积分

on 表示给于的边界条件

 

（3）其他杂项

func 表示依赖于x和y的函数

int 表示整数类型

plot 表示绘图

include 表示引用另外一个脚本文件

ofstream 表示直接输出到一个文件

ifstream 表示从一个文件读取数据

cos 余弦函数，所有经典函数都可以直接使用