转载出处:http://blog.csdn.net/eternity1118_。
1.简介
目前为止,通过MLP和BP算法的学习,我们已经接触了神经网络,并且知道了最具有代表性的一种模型“多层感知器”,这篇文章对ANN做个详细的总结和概述。
一般来讲,ANN可以看做是由大量简单计算单元(神经元节点)经过相互连接而构成的学习机器,网络中的某些因素,如连接强度(权值)、节点计算特性、网络结构等,可以按照一定的规则或算法根据样本数据来进行相应的调整(训练或学习),最终使网络实现一定的功能。
ANN的基本三要素:神经元的传递函数、网络结构、连接权值的学习算法;以上三个因素决定了不同的NN模型。
2.神经网络模型的类型
根据其结构特点,ANN模型通常被分为三大类:前馈型网络(feed-forward network)、反馈型网络(feedback network)、竞争学习型网络(competitive learning network)。
2.1前馈型网络(feed-forward network)
之前学到的BP网络就是一种前馈型的网络,这种类型网络的基本特点是,节点按照一定的层次排列,信号按照单一的方向从一层节点传递到下一层节点,网络连接是单向的,在这种分层的NN中,也可以把每一层看作是对特征进行一次加工或变换,如果节点传递函数是线性的,那么这种变换就是线性变换,反之就是非线性变换,经过一系列变换后,由网络的最后一层节点来做决策,而BP网络其实就是通过隐层节点对样本特征进行非线性变换,然后在变换空间中采用感知器准则函数构建线性分类器。
还有一种我们所熟知的网络--RBF,熟称径向基函数网络,它也是典型的前馈型,ok,在了解RBF网络之前,我们先来了解下什么是径向函数。
径向函数(radial function)是一种自变量取值仅依赖于样本到原点或到其他中心点距离的函数,通常是欧氏距离;而所谓的径向基函数(RBF)其实就是用一组径向函数的加权求和来实现某种函数逼近:
其中,ci是原点或中心点;
最常用的径向基函数是高斯函数:
其中,c是中心点,r是宽度参数;所以RBF网络就是用一个三层的神经网络来实现径向基函数的逼近,如图:
上图中,每一个输入特征都以一定的权值连接到中间层的节点,每个中间层节点是一个径向基函数,所有径向基函数又通过一定的权值连接到输出节点,对于用来作函数逼近的RBF网络,输出节点往往为线性函数;而对于用作模式识别的RBF网络,输出节点可以使阈值逻辑函数,(两类问题)如果各个径向基函数的输出加权求和后大于一定阈值,则决策为第一类,否则第二类。
该网络中主要可以调节的参数有:径向基函数的个数,每个径向基函数的中心,宽度,以及连接权值。
2.2反馈型网络(feedback network)
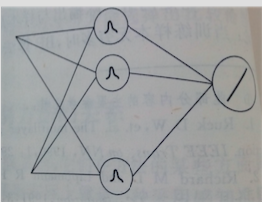
这种类型的网络中最常见的是Hopfield网络,如图:
上图中可以看出,该网络其实是一种闭环网络,与我们的反馈控制系统一样,输入信号作用到各节点上后,各个节点的输出又作为输入反馈到各节点,待网络稳定后输出。Hopfield网络多用于函数优化上,在模式识别中还可以用于特征优化及模板匹配等。
2.3竞争学习型网络(competitive learning network)
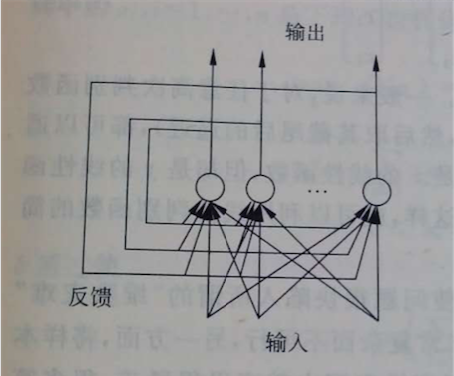
这种类型的网络跟上一种不同,没有反馈连接,且其节点都是排列在同一个层次上,所以神经网络之间会产生横向的连接或相互影响,在学习时通过神经元之间的竞争实现特定的映射,最具代表性的是自组织映射网络(熟称SOM),如图,它属于一种非监督的学习过程,后续会学习到。
当然还有其他的网络,比如模糊神经网络也很有用。
3.如何选择神经网络结构
对于任意一个复杂的非线性函数,总存在适当的MLP来以任意精度逼近它,因此MLP几乎可以看成是一种“万能”的分类器,但是这一理论只是存在性的理论,对于如何针对具体问题找到适当的NN结构却没有给出答案。在基于数据的ML中,我们面对的知识训练样本,如何设计适当的NN结构才能取得更好的效果,至今都是一个广泛被关注的重要问题,但可惜的是人们还不能很好地对这一问题给出解答。
一般的NN来说,输入节点数是样本特征的维数,输出是具体需要而定,唯独中间层的节点数以及中间层的层数是不确定的,因此我们的问题就转化为了如何确定隐层的层数和隐层的节点数。说到这里或许大家都了解,一方面,大的隐层节点数会导致强学习能力,更容易收敛到一个训练误差较小的解,但是当训练样本有限的情况下,训练误差小并不一定能保证在预测未知样本上准确性就高,这种现象叫做“过学习”或“过拟合”(over-fitting),因此盲目增加隐层节点数的做法并不可取。另一方面,小的隐层节点数自然会导致过于薄弱的学习能力,无法构成非线性复杂的分类面,对于复杂数据很难得到小的训练误差,当然在测试样本上结果也是差强人意的,这种现象就叫做“欠学习”或“欠拟合”(under-fitting)。不管是过学习还是欠学习都是不可取的,我们需要的是两者之间的平衡。
通常来说,有三种做法来选择隐层节点数和隐层数:
1)试探性选择:在缺乏理论指导的情况下,通过多次试算,往往有可能找到合适的数目,具体做法是:多选几个值,采用留一法或其它进行交叉验证,然后根据交叉验证的错误率来选择较恰当的节点数;基本经验有:a)隐层节点数要小于输入节点数,或者可以为输入节点数的一半;b)小训练样本下,选择较少的隐层节点。
2)根据先验知识 :这个就是要根据具体问题或对象的分析,针对某一个性质来设计对应的层;
3)算法确定:具有代表性的是裁减法,基本做法是:初始时采用较多的隐层节点,在采用BP进行权值学习时增加一条额外的指标,就是要求所有权值的绝对值或平方和尽可能地小,这样一来,一部分多余的节点的权值就会逐渐减小,然后在学习到某一阶段时,检查各隐层节点的权值,把那些权值太小的节点剔除掉,然后对剩下的节点再进行学习,当然这一过程也要进行多次。
对于隐层数,当然是越多越好,因为隐层越多,网络越深,学习能力也更强,但是也要具体分析。
当然,实际应用时仍然需要对具体问题和数据有个充分的认识之后,再决定如何对待。
4.神经网络与传统模式识别方法的关系
NN与传统模式识别方法之间有相互联系的,在某些方面具有等价性,如MLP其实可以看做是感知器的非线性推广,当然还有研究表明,MLP还可以看做是对贝叶斯后验概率的估计,对此有一个结论:当训练样本无穷多时,BP算法的目标函数等价于神经网络输出与样本后验概率的均方误差,最小化这样的目标函数得到的网络输出就是对样本后验概率的最小均方误差估计,当然前提是在确定的结构下。
5.神经网络如何应用于模式识别
对于非线性的模式识别,传统方法中需要给定指定功能的非线性判别函数才能设计分类器,或者分段线性,但是如果采用神经网络就会比其他模式识别方法要简单方便很多,因为对于神经网络而言它就是一个黑盒子,只要确定了其网络结构,剩下的用BP来学习训练就好了,而无需关心网络最后实现的分类器是什么样的,而且它不需要使用者对数学模型有很充分的了解,使用起来容易上手。
尽管易上手,但还是有两方面的工作要注意:1)需要利用网络的输出对分类的类别进行合理的编码;2)对特征进行标准化;
5.1输出编码
对于多类问题,常见做法为:对于c类问题,设计有c个输出节点的NN,每个节点为一类;在训练阶段,对于属于第i类的样本,设定第i个节点的期望输出为1,其余都为零。在对新样本进行识别时,考查各个输出节点,以输出最大的节点对应的类别作为对该样本的类别决策。
看起来,这种方法是不是很像之前提到的多SVM分类,因此这种做法也被称为“1-of-C”编码。
5.2特征标准化
由于神经元节点的传递函数对特征的取值范围有一定的要求限制,所以在利用NN进行模式识别时,一定要注意这个细节点,这是很多初学者极容易忽视的地方。
拿Sigmoid函数来说,值域为[0,1],而自变量取值范围为负无穷到正无穷,这种自变量过大或过小容易导致函数饱和,从而不能察觉到自变量中的变化,举个例子,如果某一特征其取值远大于1,比如200,如果直接拿这样的特征作为神经网络的输入,那么不论特征取100还是800,对神经元来说其值都近似为无穷大,尽管最后也可能会得到很接近的输出值,但是这一特征在实际分类中起不到半点作用,而且这种情况可以通过采用很小的权值来矫正,但是各连接权值之间大小差异太明显,仍然对学习的收敛有很大不利,因此为了避免这一情况,我们需要进行特征标准化,通过调整特征的scale和平移特征的均值,使得各特征的取值都位于传递函数比较敏感的自变量取值范围内。
特征标准化的做法最常用的是归一化,归一化为1或者标准差等。







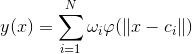















 1568
1568

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








