美赛BOOM数学建模4-2微分方程传染病预测模型

注明：本文根据数学建模BOOM网课简单整理，自用

• 指数传播模型与SI模型

❑从最简单的指数传播模型说起

❑ 传染病预测问题

• 不同类型传染病的发病机理和传播途径各有特点

• 有的传染病，在得过一次后可获得免疫力，但有的则不会

• 有的传染病具有潜伏期，有的则没有

• 需要对不同类型的传染病建立相应合适的预测模型

❑ 从最简单的看起：指数传播模型

1. 假设所研究的区域是封闭区域，在一定时期内人口总量不变，不考虑迁入和迁出

2. 在𝑡时刻患病人数𝑁(𝑡)是随时间连续变化的、可微的函数

3. 每个病人在单位时间内会传染到的人数为大于0的常数𝜆

❑ 本期课程重点：模型假设与模型改进的思想

❑指数传播模型

❑ 模型的建立

• 设𝑁(𝑡)为𝑡时刻患病人数，则𝑡 + Δ𝑡时刻的患病人数为𝑁(𝑡 + Δ𝑡)

• 则从𝑡 → 𝑡 + Δ𝑡时间内，净增的患病人数为𝑁 (t + Δ𝑡) − 𝑁(𝑡)

• 根据假设3（每个病人在单位时间内会传染到的人数为大于0的常数𝜆），有：

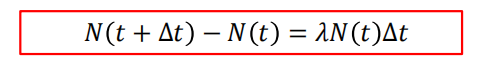
• 注意，𝜆在模型中始终是常数（每个病人在单位时间内会传染到的人数）

❑ 微分方程

• 基于上一页的第2条模型假设，在上面公式等号两边同时除以Δ𝑡，并令Δ𝑡 → 0

• 可得微分方程：

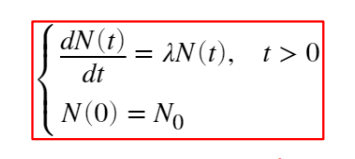
• 可求得该模型的解析解：

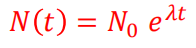
❑ 结果分析

• 模型结果显示，患病人数是指数型增长的

• 该模型一般适用于传染病暴发初期

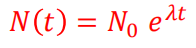
• 因为在初期，传染源和传染途径往往未知，难以防范

• 但是按照该模型， 𝑡 → ∞时𝑁（t）→ ∞，这显然是不符合实际的

❑ 模型改进

• 封闭区域内人数有限，当患病人数越来越多时，健康人群的数量也就越来越少

• 那么单位时间内新增的人数（ 𝑁（t）的导数）也会减少，毕竟没多少人可以被感染了

• 基于以上分析，对模型进行改进，建立SI模型

❑SI模型

❑ 模型假设