一文看懂如何用贝叶斯解决实际问题

贝叶斯定理太有用了，不管是在投资领域，还是机器学习，或是日常生活中高手几乎都在用到它。

生命科学家用贝叶斯定理研究基因是如何被控制的；

教育学家突然意识到，学生的学习过程其实就是贝叶斯法则的运用；

基金经理用贝叶斯法则找到投资策略；

Google用贝叶斯定理改进搜索功能，帮助用户过滤垃圾邮件；

无人驾驶汽车接收车顶传感器收集到的路况和交通数据，运用贝叶斯定理更新从地图上获得的信息；

人工智能、机器翻译中大量用到贝叶斯定理。

我准备花一个系列，从下面4个方面来科普下贝叶斯定理。前2次我们聊了：

1.贝叶斯定理有什么用？ 

2.什么是贝叶斯定理？ 

今天是第3部分：贝叶斯定理的应用案例

前面我们介绍了贝叶斯定理公式，及其背后的思想。现在我们来举个实际例子，你会更加熟悉这个牛瓣的工具。

为了后面的案例计算，我们需要先补充下面这个知识。

1   全概率公式

这个公式的作用是计算贝叶斯定理中的P(B)。

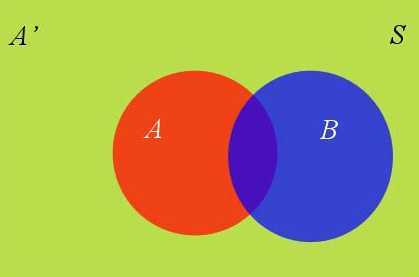
假定样本空间S，由两个事件A与A'组成的和。例如下图中，红色部分是事件A，绿色部分是事件A'，它们共同构成了样本空间S。

这时候来了个事件B，如下图：

全概率公式：

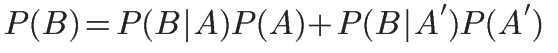
它的含义是，如果A和A'构成一个问题的全部（全部的样本空间），那么事件B的概率，就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。

看到这么复杂的公式，记不住没关系，因为我也记不住，下面用的时候翻到这里来看下就可以了。

2   贝叶斯定理在判断中的应用

有两个一模一样的碗，1号碗里有30个巧克力和10个水果糖，2号碗里有20个巧克力和20个水果糖。

然后把碗盖住。随机选择一个碗，从里面摸出一个巧克力。

问题：这颗巧克力来自1号碗的概率是多少？

好了，下面我就用套路来解决这个问题，到最后我会给出这个套路。

第1步，分解问题

1）要求解的问题：取出的巧克力，来自1号碗的概率是多少？

来自1号碗记为事件A1，来自2号碗记为事件A2

取出的是巧克力，记为事件B，

那么要求的问题就是P(A1|B)，即取出的是巧克力，来自1号碗的概率

2）已知信息：

1号碗里有30个巧克力和10个水果糖

2号碗里有20个巧克力和20个水果糖

取出的是巧克力

第2步，应用贝叶斯定理

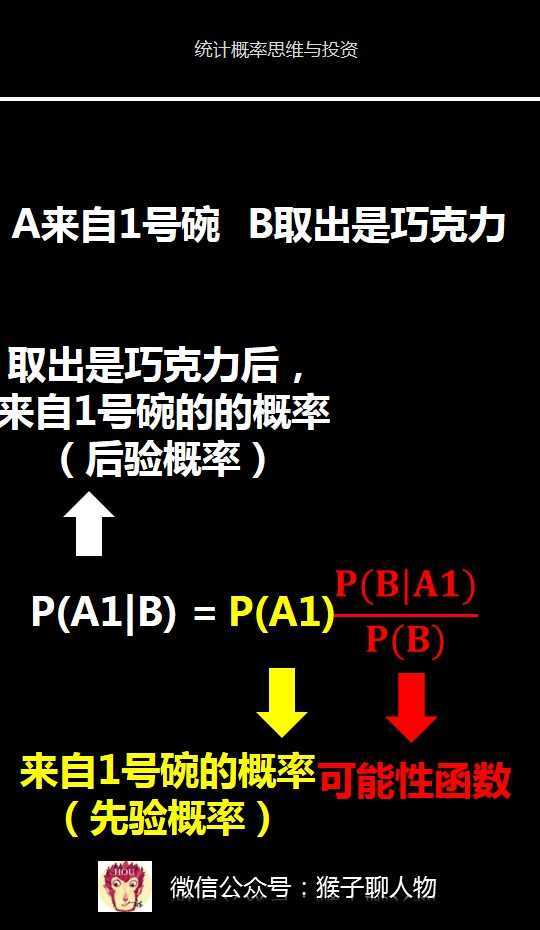
第3步，求贝叶斯中的2个指标

1）求先验概率

由于两个碗是一样的，所以在得到新信息（取出是巧克力之前），这两个碗被选中的概率相同，因此P(A1)=P(A2)=0.5,(其中A1表示来自1号碗，A2表示来自2号碗)

这个概率就是"先验概率"，即没有做实验之前，来自一号碗、二号碗的概率都是0.5。

2）求可能性函数

可能性函数P(B|A1)/P(B)

其中，P(B|A1)表示从一号碗中(A1)取出巧克力(B)的概率。

因为1号碗里有30个水果糖和10个巧克力，所以P(B|A1)=30/(30+10)=75%

现在只有求出P(B)就可以得到答案。根据全概率公式，可以求得P(B)如下图：

图中P(B|A1)是1号碗中巧克力的概率，我们根据前面的已知条件，很容易求出。

同样的，P(B|A2)是2号碗中巧克力的概率，也很容易求出（图中已给出）。

而P(A1)=P(A2)=0.5

将这些数值带入公式中就是小学生也可以算出来的事情了。最后P(B)=62.5%

所以，可能性函数P(A1|B)/P(B)=75%/62.5%=1.2

可能性函数>1.表示新信息B对事情A1的可能性增强了。

3）带入贝叶斯公式求后验概率

将上述计算结果，带入贝叶斯定理，即可算出P(A1|B)=60%

这个例子中我们需要关注的是约束条件：抓出的是巧克力。如果没有这个约束条件在，来自一号碗这件事的概率就是50%了，因为巧克力的分布不均把概率从50%提升到60%。

3   贝叶斯定理解决问题的套路

现在，我总结下刚才的贝叶斯定理应用的套路，你就更清楚了，会发现像小学生做应用题一样简单。

第1步. 分解问题

简单来说就像做应用题的感觉，先列出解决这个问题所需要的一些条件，然后记清楚哪些是已知的，哪些是未知的。

1）要求解的问题是什么？

识别出哪个是贝叶斯中的事件A（一般是想要知道的问题），哪个是事件B（一般是新的信息，或者实验结果）

2）已知条件是什么？

第2步.应用贝叶斯定理

第3步，求贝叶斯公式中的2个指标

1）求先验概率

2）求可能性函数

3）带入贝叶斯公式求后验概率

后面我会接着聊以下内容：

3.应用案例2：贝叶斯在疾病检测中的应用

4.生活中的贝叶斯思维