一、设计目的
1.斜抛物体的水平射程和竖直射高的数值分析。
2.物体斜抛的初速度为 v0 ,不计空气阻力,求物体的水平射程和竖直射高与射角的关系。求证:物体轨迹的最高点都分布在一个椭圆上。
二、设计思路
物体的水平射程和竖直射高与射角之间存在一定的关系。我们可以通过分析轨迹方程来求证物体轨迹的最高点都分布在一个椭圆上。
假设物体的初速度为v₀,射角为θ。
在水平方向上,物体的速度恒定,即vₓ = v₀ * cosθ。假设物体的飞行时间为t,根据匀速直线运动的公式可以得到水平射程:
R = vₓ * t
= v₀ * cosθ * t
在竖直方向上,物体受到重力加速度g的影响。假设物体的竖直飞行时间为t,竖直方向的位移为h,竖直方向的初速度为vy0。
根据竖直方向上的运动学公式可以得到:
h = vy0 * t + (1/2) * g * t²
由于初速度v₀在初速度方向上的投影为vᵧ = v₀ * sinθ,且在竖直方向上初速度为vy0 = vᵧ。
代入上述关系,我们可以得到:
h = v₀ * sinθ * t - (1/2) * g * t²
因为物体在达到最高点时,竖直方向的速度为0,即vᵧ = 0。
根据上述条件可以得到:
vy0 = 0
vy0 = v₀ * sinθ - g * t
解得 t = (v₀ * sinθ) / g
将t代入h的表达式中可以得到:
h = (v₀ * sinθ) * (v₀ * sinθ) / (2g)
接下来,我们可以推导物体轨迹的方程。
在水平方向上,物体的运动可以表示为:
x = vx0 * t= (v₀ * cosθ) * t
在竖直方向上,物体的运动可以表示为:
y = h + h0
= (v₀ * sinθ) * (v₀ * sinθ) / (2g) + 0
= (v₀ * sinθ)² / (2g)
将x和y的表达式结合起来,我们可以得到物体轨迹的方程:
(x² / (v₀ * cosθ)) + (y² / ((v₀ * sinθ)² / (2g))) = 1
这是一个标准的椭圆方程,表明物体轨迹的最高点位于椭圆的焦点位置。
因此,我们可以证明物体轨迹的最高点都分布在一个椭圆上。
三、代码及结果
%斜抛物体的射程,射局和最局点的分布
clear%清除变量
theta=0:90;%物体射角的度数向量
th=theta*pi/180;%物体射角的弧度数
x=sin(2*th);%水平射程(以最大射程为单位)
y=sin(th).^2/2;%竖直射高(以最大射程为单位)
figure%创建图形窗口
plot(theta,x,theta,y,'--','linewidth' ,2)%画射程和射高曲线
grid on%加网格
legend('射程\itX/X\rm_M','射高\itY/X\rm_M')%图例
fs=16;%字体大小
title('斜抛物体的水平射程和竖直射高','FontSize',fs)%标题
xlabel('射角\it\theta/\rm\circ','FontSize' ,fs)%横坐标标签
text(0,0.5,'\itX\rm_M=\itv\rm_0^2/\itg','FontSize',fs)%说明最大射程
theta= 15:10:75;%物体射角的度数向量
th=theta*pi/180;%物体射角的弧度数
x=linspace(0,1,40);%水平坐标向量(以最大射程为单位)
[TH,X]=meshgrid(th,x);%水平坐标和角度和矩阵
Y=X.*tan(TH)-X.^2/2./cos(TH).^2;%高度位置矩阵
figure%创建图形窗
%plot(x,Y,'LineWidth',2) %画斜抛运动曲线族
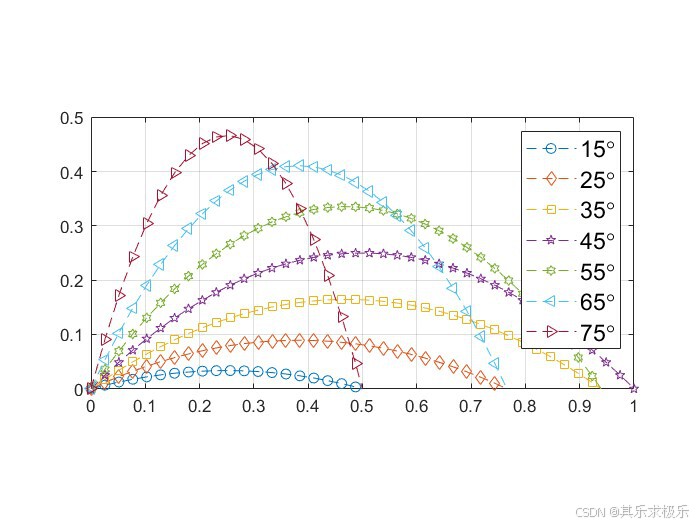
plot(x,Y(:,1),'o-',x,Y(:,2),'d-',x,Y(:,3),'s-',x,Y(:,4),'p-',...
x,Y(:,5),'h-',x,Y(:,6),' <-',x,Y(:,7),'>-','LineStyle','--')%画斜抛运动曲线族
grid on %加网格
axis equal %使坐标刻度相等
axis([0 1 0 0.5]) %曲线范围
n=length(th); %射角的个数
h=legend([num2str(theta'),repmat('\circ',n,1)]);%插入角度图例
set(h,'FontSize' ,fs-2)%放大图例
y0=zeros(size(h));%落点纵坐标向量
x0=sin(2*th);%落点横坐标向量(射高的横坐标的两倍)
text(x0,y0,num2str(x0',3),'FontSize',fs)%标记射程(保留3位)
ym= sin(th).^2/2;%射高
text(x0/2,ym,num2str(ym',3),'FontSize',fs)%标记射高(保留3位)
hold on%保持图像
plot([y0;x0/2],[ym;ym],'--')%画射高的水平虚线
stem(x0/2,ym,'--','filled')%画直杆虚线作为射高的竖直线
ym=0:0.01:0.5;%最高点的纵坐标
xm=0.5*sqrt(1-((ym-0.25)/0.25).^2); %最高点的横坐标
plot(xm,ym,LineWidth',2)%画最大高度曲线
title('斜抛物体的曲线和最高点的分布','FontSize',fs)%标题
xlabel('水平坐标\itx/X\rn_ I','FontSize' ,fs)%横坐标标签
ylabel('竖直坐标\ity/X\rm_ I','FontSize' ,fs)%纵坐标标签
text(0.6,0.4,'\itX\rm_ M=\itv\rm.0^2/\itg','FontSize',fs)%说明最大射程 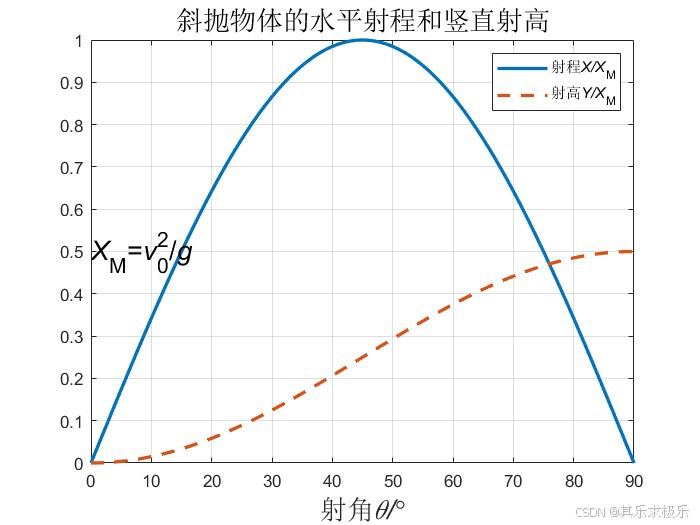

























 542
542

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








