【模板】点双连通分量
题目描述
对于一个 n n n 个节点 m m m 条无向边的图,请输出其点双连通分量的个数,并且输出每个点双连通分量。
输入格式
第一行,两个整数 n n n 和 m m m。
接下来 m m m 行,每行两个整数 u , v u, v u,v,表示一条无向边。
输出格式
第一行一个整数 x x x 表示点双连通分量的个数。
接下来的 x x x 行,每行第一个数 a a a 表示该分量结点个数,然后 a a a 个数,描述一个点双连通分量。
你可以以任意顺序输出点双连通分量与点双连通分量内的结点。
样例 #1
样例输入 #1
5 8
1 3
2 4
4 3
1 2
4 5
5 1
2 4
1 1
样例输出 #1
1
5 1 2 3 4 5
样例 #2
样例输入 #2
5 3
1 2
2 3
1 3
样例输出 #2
3
1 4
1 5
3 1 2 3
样例 #3
样例输入 #3
6 5
1 3
2 4
1 2
4 6
2 3
样例输出 #3
4
2 6 4
2 4 2
3 3 2 1
1 5
样例 #4
样例输入 #4
7 8
1 3
2 4
3 5
2 5
6 4
2 5
6 3
2 7
样例输出 #4
3
2 7 2
5 5 2 4 6 3
2 3 1
样例 #5
样例输入 #5
1 1
1 1
样例输出 #5
1
1 1
提示
样例四解释:
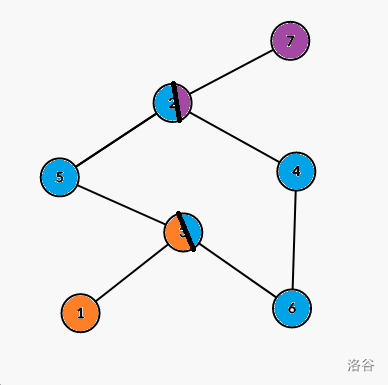
相同颜色的点为同一个分量里的结点。
温馨提示:请认真考虑孤立点与自环(样例五)的情况。
数据范围:
对于
100
%
100\%
100% 的数据,
1
≤
n
≤
5
×
1
0
5
1 \le n \le 5 \times10 ^5
1≤n≤5×105,
1
≤
m
≤
2
×
1
0
6
1 \le m \le 2 \times 10^6
1≤m≤2×106。
| subtask | n n n | m m m | 分值 |
|---|---|---|---|
| 1 1 1 | 1 ≤ n ≤ 100 1 \le n \le 100 1≤n≤100 | 1 ≤ m ≤ 500 1 \le m \le 500 1≤m≤500 | 25 25 25 |
| 2 2 2 | 1 ≤ n ≤ 5000 1 \le n \le 5000 1≤n≤5000 | 1 ≤ m ≤ 5 × 1 0 4 1 \le m \le 5 \times 10^4 1≤m≤5×104 | 25 25 25 |
| 3 3 3 | 1 ≤ n ≤ 2 × 1 0 5 1 \le n \le 2\times 10^5 1≤n≤2×105 | 1 ≤ m ≤ 5 × 1 0 5 1 \le m \le 5\times 10^5 1≤m≤5×105 | 25 25 25 |
| 4 4 4 | 1 ≤ n ≤ 5 × 1 0 5 1 \le n \le 5 \times10 ^5 1≤n≤5×105 | 1 ≤ m ≤ 2 × 1 0 6 1 \le m \le 2 \times 10^6 1≤m≤2×106 | 25 25 25 |
本题不卡常,时间限制与空间限制均已开大,正确的解法均可通过。
数据更新
- 2022 / 7 / 14 2022/7/14 2022/7/14 加强数据
- 2022 / 11 / 26 2022/11/26 2022/11/26 新增 10 10 10 组较小的数据( 1 ≤ n , m ≤ 10 1\le n, m \le 10 1≤n,m≤10),方便选手调试。
- 2022 / 12 / 31 2022/12/31 2022/12/31 重组 s u b t a s k subtask subtask,并加入若干组极端数据。
- 2023 / 1 / 1 2023/1/1 2023/1/1 发现昨天新加入的数据出了问题,已修改。
惊喜:AC 后记得把鼠标放到测试点上看反馈信息,有惊喜哦。
七月二十一号更新:更正了一处笔误。
先介绍几个概念:
连通分量:无向图中,满足任意两点之间都有路径相连的极大连通子图。也就是说,抽离出一些点以及它们之间的边,满足这些点任意两点之间,可以直接或间接到达对方,在这个前提下,满足抽离出的图越大越好,把抽离出的图叫做连通分量。
割点:无向图中,删除该点及与其相连的边后,图的连通分量数量增加,则称其为割点。换而言之,删除一个割点及相关边后,图中原来连通的两点不再连通,从而使得一个连通分量分裂成两个(或多个)连通分量。
点双连通:若对于一个无向图,其任意一个节点对于这个图本身而言都不是割点,则称其点双连通。也就是说,删除任意点及其相关边后,整个图仍然属于一个连通分量。
点双连通分量:无向图中,极大的点双连通子图。与连通分量类似,抽离出一些点及它们之间的边,使得抽离出的图是一个点双连通图,在这个前提下,使得抽离出的图越大越好。
先讲讲怎么求割点:
引入 Tarjan 算法。
我们把 DFS 遍历无向图过程中形成的图叫做搜索树,其中,从 uuu 到一个未被搜索过的节点 vvv 的一条边叫树边,回溯到一个祖先 vvv 的边叫返祖边。
定义 dfnudfn_udfnu 表示 uuu 在搜索树中的访问时间戳(第几个搜到),lowulow_ulowu 表示 uuu 通过返祖边可回溯到的最小时间戳。
初始时,lowu=dfnulow_u=dfn_ulowu=dfnu。
对于一条树边 (u,v)(u,v)(u,v),lowu=min{lowv,lowu}low_u=\min\{low_v,low_u\}lowu=min{lowv,lowu},即:可以先下到 vvv,再回溯。
对于一条返祖边 (u,v)(u,v)(u,v),且 vvv 不是 uuu 的直系父亲,lowu=min{dfnv,lowu}low_u = \min\{dfn_v, low_u\}lowu=min{dfnv,lowu},即:直接回溯。
对于树边 (u,v)(u,v)(u,v),如果 lowv≥dfnulow_v\geq dfn_ulowv≥dfnu,即 vvv 和其子树能够通过返祖边回溯到的时间戳最小只能是 dfnudfn_udfnu,那么要把它们的时间戳回溯到到 dfnudfn_udfnu 之前就需要与 uuu 相关的边。也就是说这时如果把 uuu 去掉,与其有关的边全部消失,那么 lowvlow_vlowv 不可能小于等于 dfnudfn_udfnu,也就是不可能回溯到时间戳比 uuu 更小的点,此时这个子树与其它点无法连通,uuu 就是割点。
注意:一个连通分量的搜索树的根节点一定满足上面的条件,因为在这个搜索树中,不存在一个 dfndfndfn 值比它小的节点,但是当且仅当其至少拥有两个以上的子树,它才能被称为割点。
画个图吧(红色代表根节点,圆角矩形代表一个子树):
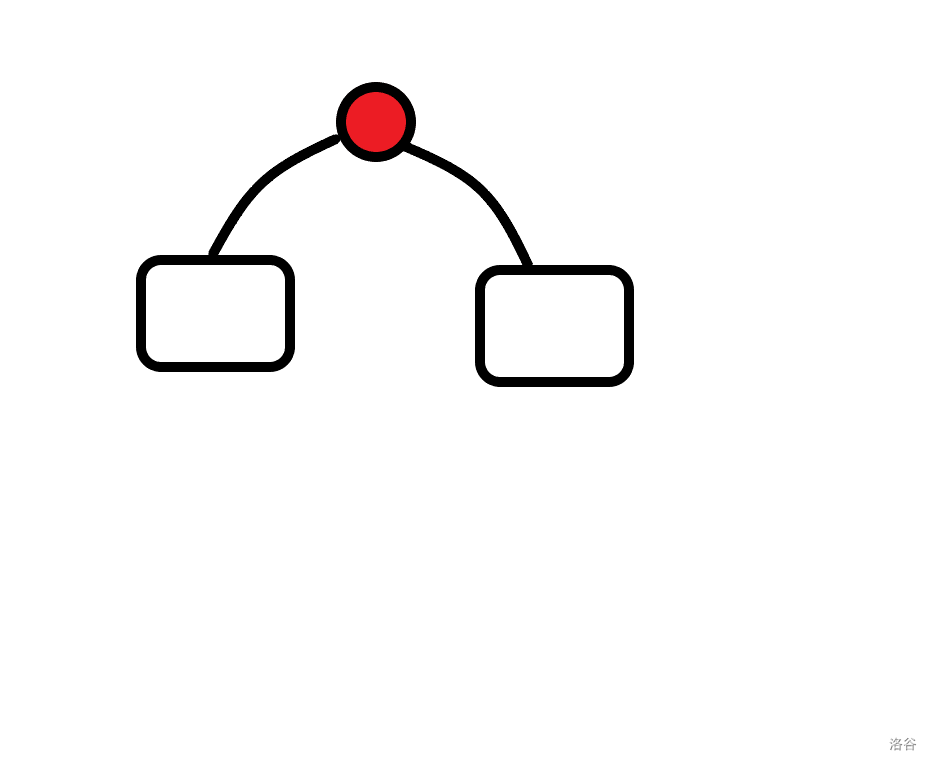
显然如果这个图只存在根节点和其中一个子树时,由于根节点是第一访问的节点,它会被我们上面的判断条件误判为割点,但是它并不是一个割点,而当它有多个子树时,删除它会使得子树不再连通,这时它才是一个割点。
代码(核心部分):
inline void tarjan(int u, int fa) {
int son = 0;//子树个数
low[u] = dfn[u] = ++idx;//打上时间戳标记
s[++top] = u;//u进入搜索树
for(int i = fir[u]; i; i = nxt[i]) {
int v = to[i];
if(!dfn[v]) {//树边
son++;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) cut[u] = true;
} else if(v != fa) low[u] = min(low[u], dfn[v]);//返祖边
}
if(fa == 0 && son < 2) cut[u] = false;//是根节点,且子树小于2,不是割点
}
知道了割点怎么求,点双连通分量(接下来简称点双)就很好求了:
两个点双最多只有一个公共点(即都有边与之相连的点);且这个点在这两个点双和它形成的子图中是割点。
对于第一点,因为当它们有两个及以上公共点时,它们可以合并为一个新的点双(矩形代表一个点双,圆形代表公共点):
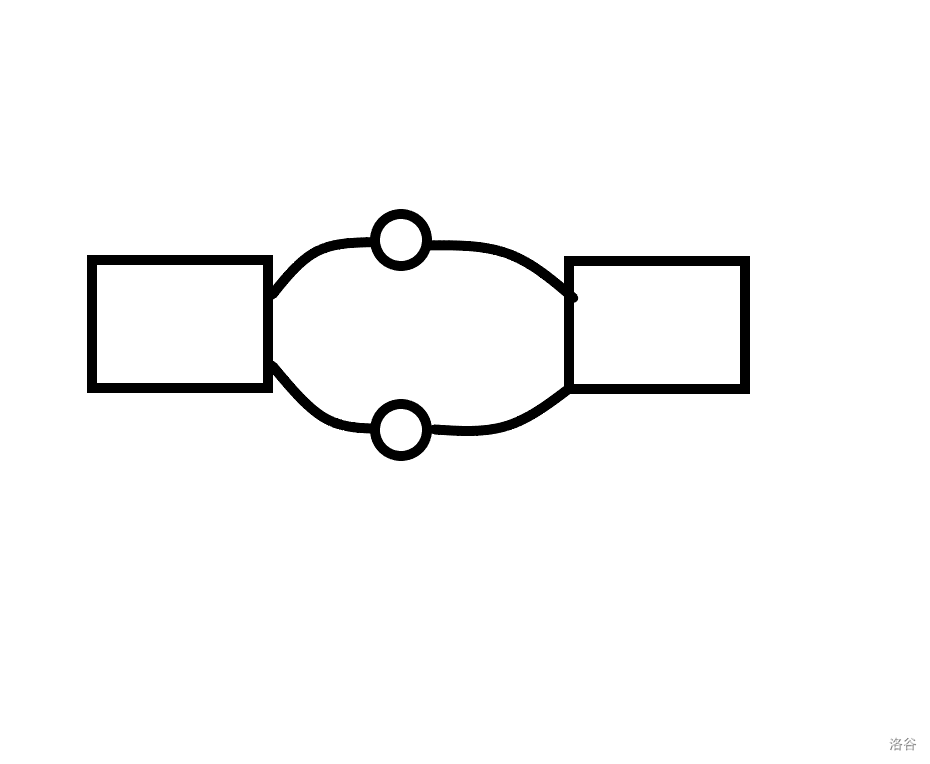
当有两个及以上公共点时,删除其中一个点及其与两个点双相连的边后,这两个点双总是可以通过另一个公共点到达彼此,属于一个连通分量,所以这些公共点对于这个子图而言并不是一个割点,按照定义,这两个点双和这些公共点应该是一个更大的点双。
对于第二点,与第一点类似,当对于这个子图而言它不是一个割点时,这两个点双也可以合并为一个新的点双:
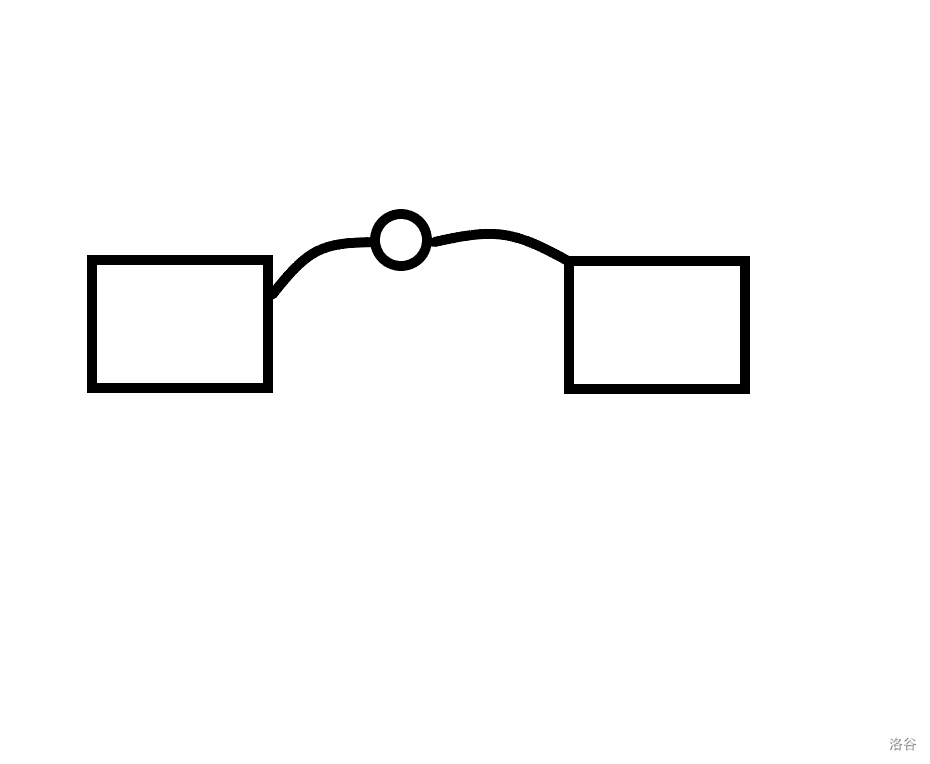
当这个公共点对于这个子图不是一个割点时,也就意味着这两个点双有着另外的边相连,而这些边相连的点同样也是两个点双的公共点,可以归到第一种情况里。
对于一个点双,它在 DFS 搜索树中 dfndfndfn 值最小的点一定是割点或者树根。
当这个点是割点时,它所属的点双必定不可以向它的父亲方向包括更多点,因为一旦回溯,它就成为了新的子图的一个割点,不是点双。所以它应该归到其中一个或多个子树里的点双中。
当这个点是树根时,它的 dfndfndfn 值是整棵树里最小的。它若有两个以上子树,那么它是一个割点;它若只有一个子树,它一定属于它的直系儿子的点双,因为包括它;它若是一个独立点,视作一个单独的点双。
换句话说,一个点双一定在这两类点的子树中。
我们用栈维护点,当遇到这两类点时,将子树内目前不属于其它点双的非割点或在子树中的割点归到一个新的点双。注意这个点可能还是与其它点双的公共点,所以不能将其出栈。
本题代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5, M = 4e6 + 5;
int cnt = 1, fir[N], nxt[M], to[M];
int s[M], top, bcc, low[N], dfn[N], idx, n, m;
vector<int> ans[N];
inline void tarjan(int u, int fa) {
int son = 0;
low[u] = dfn[u] = ++idx;
s[++top] = u;
for(int i = fir[u]; i; i = nxt[i]) {
int v = to[i];
if(!dfn[v]) {
son++;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) {
bcc++;
while(s[top + 1] != v) ans[bcc].push_back(s[top--]);//将子树出栈
ans[bcc].push_back(u);//把割点/树根也丢到点双里
}
} else if(v != fa) low[u] = min(low[u], dfn[v]);
}
if(fa == 0 && son == 0) ans[++bcc].push_back(u);//特判独立点
}
inline void add(int u, int v) {
to[++cnt] = v;
nxt[cnt] = fir[u];
fir[u] = cnt;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++) {
int u, v;
scanf("%d%d", &u, &v);
add(u, v), add(v, u);
}
for(int i = 1; i <= n; i++) {
if(dfn[i]) continue;
top = 0;
tarjan(i, 0);
}
printf("%d\n", bcc);
for(int i = 1; i <= bcc; i++) {
printf("%d ", ans[i].size());
for(int j : ans[i]) printf("%d ", j);
printf("\n");
}
return 0;
}























 714
714

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










