python numpy 从零实现简单神经网络

numpy从0实现两层神经网络及数学推导，主要涉及矩阵相乘和链式求导以及几个常见的激活函数形式。

1.logistics regression

可以把logistics单元看作是最简单的神经网络，具体这里就不在介绍了，可以看这篇文章

2.neural network

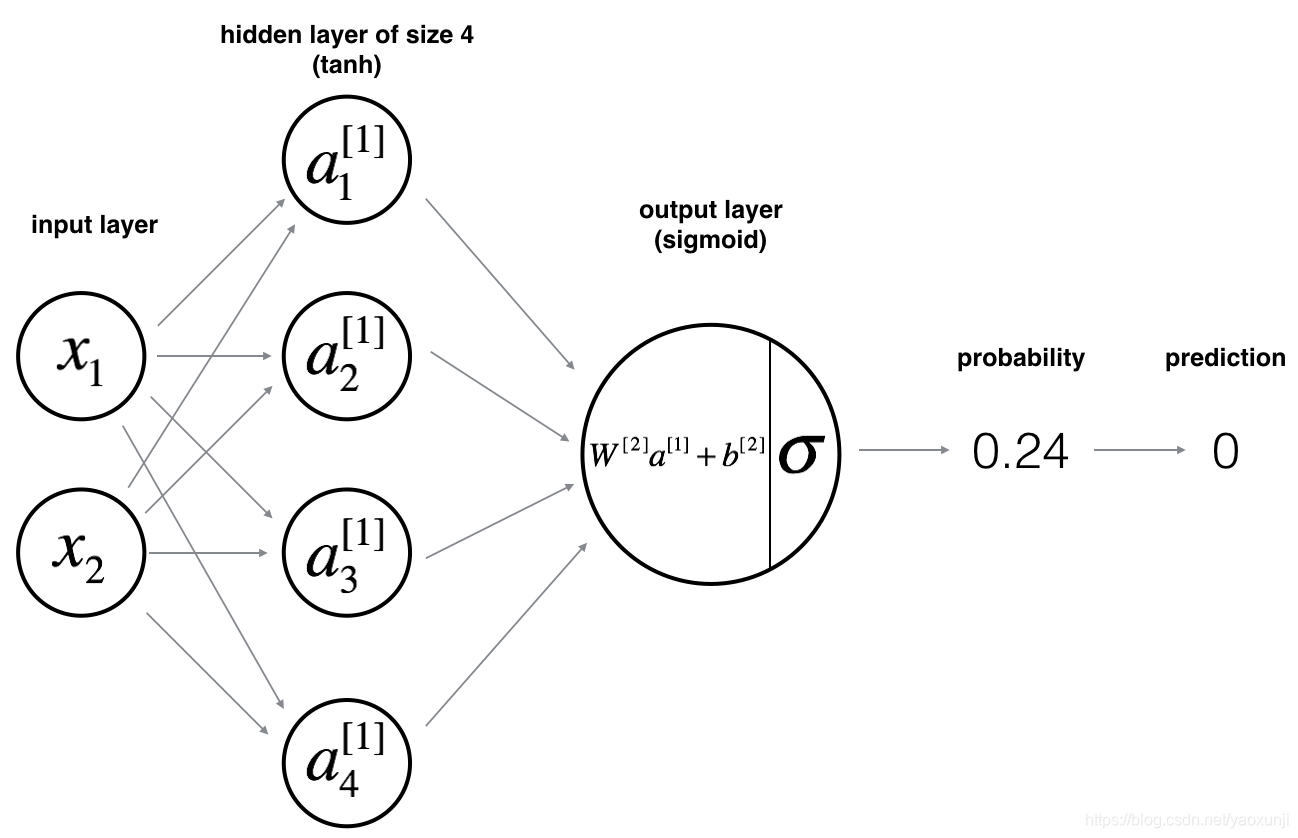
这里网络分为三层，输入层，隐含层，输出层。以图中为例来使用numpy实现前向传播，反向传播和梯度更新。

3.activation function

激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中，引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

（1） sigmoid

$$\begin{gathered} g(x)=\frac{1}{1+e^{-x}} \\ g(x{)}^{\prime }=g(x)(1-g(x)) \end{gathered}$$

numpy实现：

def sigmoid(x):
    return 1 / (1+np.exp(-x))

（2） tanh

$$\begin{gathered} g(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \\ g(x{)}^{\prime }=1-g(x{)}^2 \end{gathered}$$

numpy实现

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

4.loss function

损失函数（loss function）是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“风险”或“损失”的函数。在应用中，损失函数通常作为学习准则与优化问题相联系，即通过最小化损失函数求解和评估模型。

Cross Entropy

交叉熵损失是分类任务中的常用损失函数 ,可以用在二分类和多分类中，形式有所不同。

二分类中：
$$L(\hat{y},y)=-(ylog(\hat{y})+(1-y)log(1-\hat{y}))$$
多分类中：
$$L(\hat{y},y)=-y_{i}log(\widehat{y_i})$$

5.forward propagation

（1）初始化参数

首先网络中除去输入层还有两层，也就是我们需要初始化隐含层的权重W和偏置b，输出层的权重W和偏置b。每层权重初始化为随机数，偏置设置为0.
$$\begin{gathered} W1--(n_h,n_x),b1--(n_h,1) \\ W2--(n_y,n_h),b2--(n_y,1) \\ {n}_x--输入层，n_h--隐含层，n_y--输出层 \end{gathered}$$
numpy实现

def init_parameters(input_size,hidden_size,output_size):
    w1 = np.random.rand(hidden_size,input_size) * 0.01
    b1 = np.zeros((hidden_size,1))
    w2 = np.random.rand(output_size,hidden_size) * 0.01
    b2 = np.zeros((output_size,1))
    
    parameters = {
        "w1":w1,
        "b1":b1,
        "w2":w2,
        "b2":b2
    }
    return parameters

（2）前向传播

计算公式：
$$\begin{gathered} z^{[1](i)}=W^{[1]}{x}^{(i)}+b^{[1](i)} \\ {a}^{[1](i)}=\tanh (z^{[1](i)}) \\ {z}^{[2](i)}=W^{[2]}{a}^{[1](i)}+b^{[2](i)} \\ {\hat{y}}^{(i)}=a^{[2](i)}=sigmoid(z^{[2](i)}) \end{gathered}$$
numpy实现

def forward_propagation(X,parameters):
    w1 = parameters["w1"]
    b1 = parameters["b1"]
    w2 = parameters["w2"]
    b2 = parameters["b2"]
    
    Z1 = np.dot(w1,X) + b1
    A1 = tanh(Z1)
    
    Z2 = np.dot(w2,A1) + b2
    A2 = sigmoid(Z2)
    
    cache = {
        "Z1":Z1,
        "A1":A1,
        "Z2":Z2,
        "A2":A2,
    }
    return A2,cache

6.background propagation

（1）计算损失

$$J=-\frac{1}{m}\sum _{i=0}^m\left(y^{(i)}\log \left(a^{[2](i)}\right)+(1-y^{(i)})\log \left(1-a^{[2](i)}\right)\right)$$

numpy实现

def compute_cost(A2,Y):
    m = Y.shape[1]
    loss = -(np.multiply(Y,np.log(A2)) + np.multiply(1-Y,np.log(1-A2)))
    cost = np.sum(loss) / m
    cost = np.squeeze(cost)
    return cost

（2）反向传播

$$\begin{gathered} dW1=\frac{\partial \mathcal{J}}{\partial W_1}db1=\frac{\partial \mathcal{J}}{\partial b_1} \\ dW2=\frac{\partial \mathcal{J}}{\partial W_2}db2=\frac{\partial \mathcal{J}}{\partial b_2} \end{gathered}$$

$$\begin{gathered} 对输出层求偏导 \\ \frac{\partial \mathcal{J}}{\partial z_2^{(i)}}=\frac{1}{m}(a^{[2](i)}-y^{(i)})\frac{\partial \mathcal{J}}{\partial W_2}=\frac{\partial \mathcal{J}}{\partial z_2^{(i)}}{a}^{[1](i)T}\frac{\partial \mathcal{J}}{\partial b_2}=\sum _i\frac{\partial \mathcal{J}}{\partial z_2^{(i)}} \\ 对隐含层求偏导 \\ \frac{\partial \mathcal{J}}{\partial z_1^{(i)}}=W_2^T\frac{\partial \mathcal{J}}{\partial z_2^{(i)}}\ast (1-a^{[1](i)2})\frac{\partial \mathcal{J}}{\partial W_1}=\frac{\partial \mathcal{J}}{\partial z_1^{(i)}}{X}^T\frac{\partial {\mathcal{J}}_i}{\partial b_1}=\sum _i\frac{\partial \mathcal{J}}{\partial z_1^{(i)}} \end{gathered}$$

numpy实现

def back_propagation(parameters, cache, X, Y):
    w1 = parameters["w1"]
    b1 = parameters["b1"]
    w2 = parameters["w2"]
    b2 = parameters["b2"]
    
    Z1 = cache["Z1"]
    A1 = cache["A1"]
    Z2 = cache["Z2"]
    A2 = cache["A2"]
    
    dZ2 = A2 - Y
    dw2 = np.dot(dZ2,A1.T) / m
    db2 = np.sum(dZ2, axis=1, keepdims=True) / m
    dZ1 = np.multiply(np.dot(w2.T, dZ2), 1 - np.power(A1, 2))
    dw1 = np.dot(dZ1,X.T) / m
    db1 = np.sum(dZ1, axis=1, keepdims=True) / m
    
    grads = {"dw1": dw1,
             "db1": db1,
             "dw2": dw2,
             "db2": db2}
    
    return grads

7.gradient descent

梯度更新规则：
$$\begin{gathered} \theta =\theta -\alpha \frac{\partial J}{\partial \theta } \\ \alpha 为学习率,\theta 代表参数 \end{gathered}$$
更新公式：
$$\begin{gathered} W1:=W1-\alpha \frac{\partial \mathcal{J}}{\partial W_1} \\ b1:=b1-\alpha \frac{\partial \mathcal{J}}{\partial b_1} \\ W2:=W2-\alpha \frac{\partial \mathcal{J}}{\partial W_2} \\ b2:=b2-\alpha \frac{\partial \mathcal{J}}{\partial b_2} \end{gathered}$$
numpy实现

def gradient_descent(parameters, grads, learning_rate):
    w1 = parameters["w1"]
    b1 = parameters["b1"]
    w2 = parameters["w2"]
    b2 = parameters["b2"]
    
    dw1 = grads["dw1"]
    db1 = grads["db1"]
    dw2 = grads["dw2"]
    db2 = grads["db2"]
    
    w1 = w1 - learning_rate * dw1
    b1 = b1 - learning_rate * db1
    w2 = w2 - learning_rate * dw2
    b2 = b2 - learning_rate * db2
    
    parameters = {
        "w1":w1,
        "b1":b1,
        "w2":w2,
        "b2":b2
    }
    return parameters

8.训练网络

def model(X,Y,hidden_size,num_iterations):
    input_size = X.shape[0]
    output_size = Y.shape[0]
    parameters = init_parameters(input_size,hidden_size,output_size)
    
    for i in range(num_iterations):
        A2,cache = forward_propagation(X,parameters)
        cost = compute_cost(A2,Y)
        grads = back_propagation(parameters,cache,X,Y)
        parameters = gradient_descent(parameters,grads,0.5)
        
        if i % 1000 == 0:
            print("step:%i   %f"%(i,cost))
    return parameters

X_assess, Y_assess = nn_model_test_case() #加载训练数据
parameters = model(X_assess, Y_assess, 4, 10000)

执行结果：

step:0   0.693230
step:1000   0.642704
step:2000   0.451822
step:3000   0.128380
step:4000   0.055486
step:5000   0.033372
step:6000   0.023442
step:7000   0.017932
step:8000   0.014464
step:9000   0.012093