作者:桂。
时间:2017-03-21 07:25:17
链接:http://www.cnblogs.com/xingshansi/p/6592599.html
前言
本文为曲线拟合与分布拟合系列的一部分,主要讲解混合拉普拉斯分布(Laplace Mixture Model,LMM)。拉普拉斯也是常用的统计概率模型之一,网上关于混合高斯模型(GMM)的例子很多,而关于LMM实现的很少。其实混合模型都可以用EM算法推导,只是求闭式解的运算上略有差别,全文包括:
1)LMM理论推导;
2)LMM代码实现;
内容多有借鉴他人,最后一并附上链接。
一、LMM理论推导
A-模型介绍
对于单个拉普拉斯分布,表达式为:

















对于
 个模型的混合分布:
个模型的混合分布:



























如何拟合呢?下面利用EM分析迭代公式,仅分析Y为一维的情况,其他可类推。(先给出一个结果图)

B-EM算法推导
E-Step:
1)求解隐变量,构造完全数据集
同GMM推导类似,利用全概率公式:

2)构造Q函数
基于之前混合高斯模型(GMM)的讨论,EM算法下混合模型的Q函数可以表示为:


























































































其中









 为分布
为分布
 对应的参数,
对应的参数,
 = {
= {

 ,
,

 ,...,
,...,

 }为参数集合,
}为参数集合,
 为样本个数,
为样本个数,
 为混合模型个数。
为混合模型个数。
M-Step:
1)MLE求参
- 首先对

 进行优化
进行优化
由于








 ,利用Lagrange乘子求解:
,利用Lagrange乘子求解:



















































求偏导:





































得

- 对各分布内部参数

 进行优化
进行优化
给出准则函数:

















































仅讨论

 为一维数据情况,其他类推。对于拉普拉斯分布:
为一维数据情况,其他类推。对于拉普拉斯分布:

关于

 利用MLE即可求参。
利用MLE即可求参。
首先求解

 的迭代公式:
的迭代公式:

由于

 含有绝对值,因此需要一点小技巧。
含有绝对值,因此需要一点小技巧。

 对
对

 求偏导,得到:
求偏导,得到:
![]()
得到的

 估计即为:
估计即为:











在迭代的最终状态,可以认为
 次参数与
次参数与


 次参数近似相等,从而上面的求导结果转化为:
次参数近似相等,从而上面的求导结果转化为:

得到参数

 的迭代公式:
的迭代公式:

总结一下LMM的求解步骤:
E-Step:
M-Step:
二、LMM代码实现
根据上一篇GMM的代码,简单改几行code,即可得到LMM:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
function
[u,b,t,iter] = fit_mix_laplace( X,M )
%
% fit_mix_laplace - fit parameters for a mixed-laplacian distribution using EM algorithm
%
% format: [u,b,t,iter] = fit_mix_laplacian( X,M )
%
% input: X - input samples, Nx1 vector
% M - number of gaussians which are assumed to compose the distribution
%
% output: u - fitted mean for each laplacian
% b - fitted standard deviation for each laplacian
% t - probability of each laplacian in the complete distribution
% iter- number of iterations done by the function
%
N =
length
( X );
Z =
ones
(N,M) * 1/M;
% indicators vector
P =
zeros
(N,M);
% probabilities vector for each sample and each model
t =
ones
(1,M) * 1/M;
% distribution of the gaussian models in the samples
u =
linspace
(0.2,1.4,M);
% mean vector
b =
ones
(1,M) *
var
(X) /
sqrt
(M);
% variance vector
C = 1/
sqrt
(2*
pi
);
% just a constant
Ic =
ones
(N,1);
% - enable a row replication by the * operator
Ir =
ones
(1,M);
% - enable a column replication by the * operator
Q =
zeros
(N,M);
% user variable to determine when we have converged to a steady solution
thresh = 1e-7;
step = N;
last_step = 300;
% step/last_step
iter = 0;
min_iter = 3000;
while
(((
abs
((step/last_step)-1) > thresh) & (step>(N*1e-10)) ) & (iter<min_iter) )
% E step
% ========
Q = Z;
P = 1./ (Ic*b) .*
exp
( -(1e-6+
abs
(X*Ir - Ic*u))./(Ic*b) );
for
m = 1:M
Z(:,m) = (P(:,m)*t(m))./(P*t(:));
end
% estimate convergence step size and update iteration number
prog_text =
sprintf
(
repmat
(
'\b'
,1,(iter>0)*12+
ceil
(
log10
(iter+1)) ));
iter = iter + 1;
last_step = step * (1 +
eps
) +
eps
;
step =
sum
(
sum
(
abs
(Q-Z)));
fprintf
(
'%s%d iterations\n'
,prog_text,iter );
% M step
% ========
Zm =
sum
(Z);
% sum each column
Zm(
find
(Zm==0)) =
eps
;
% avoid devision by zero
u =
sum
(((X*Ir)./
abs
(X*Ir - Ic*u)).*Z) ./
sum
(1./
abs
(X*Ir - Ic*u).*Z) ;
b =
sum
((
abs
(X*Ir - Ic*u)).*Z) ./ Zm ;
t = Zm/N;
end
end
|
给出上文统计分布的拟合程序:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
clc
;
clear
all
;
%generate random
xmin = -10;
xmax = 10;
Len = 10000000;
x =
linspace
(xmin,xmax,Len);
mu = [3,-4];
b = [0.9 0.4];
w = [0.7 0.3];
fx = w(1)/2/b(1)*
exp
(-
abs
(x-mu(1))/b(1))+ w(2)/2/b(2)*
exp
(-
abs
(x-mu(2))/b(2));
ymax = 1/b(2);
ymin = 0;
Y = (ymax-ymin)*
rand
(1,Len)-ymin;
data = x(Y<=fx);
%Laplace Mixture Model fitting
K = 2;
[mu_new,b_new,w_new,iter] = fit_mix_laplace( data',K);
%figure
subplot
221
hist
(data,2000);
grid
on;
subplot
222
numter = [xmin:.2:xmax];
plot
(numter,w_new(1)/2/b_new(1)*
exp
(-
abs
(numter-mu_new(1))/b_new(1)),
'r'
,
'linewidth'
,2);
hold
on;
plot
(numter,w_new(2)/2/b_new(2)*
exp
(-
abs
(numter-mu_new(2))/b_new(2)),
'g'
,
'linewidth'
,2);
hold
on;
subplot
(2,2,[3,4])
[histFreq, histXout] =
hist
(data, numter);
binWidth = histXout(2)-histXout(1);
%Bar
bar
(histXout, histFreq/binWidth/
sum
(histFreq));
hold
on;
grid
on;
plot
(numter,w_new(1)/2/b_new(1)*
exp
(-
abs
(numter-mu_new(1))/b_new(1)),
'r'
,
'linewidth'
,2);
hold
on;
plot
(numter,w_new(2)/2/b_new(2)*
exp
(-
abs
(numter-mu_new(2))/b_new(2)),
'g'
,
'linewidth'
,2);
hold
on;
|
对应结果图(与上文同):

参考
- Mitianoudis N, Stathaki T. Batch and online underdetermined source separation using Laplacian mixture models[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(6): 1818-1832.








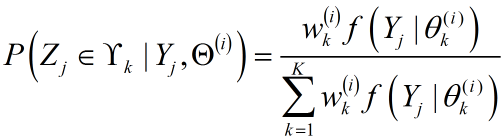



















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








