线段树初步

1、综述

假设有编号从1到 $n$ 的 $n$ 个点，每个点都存了一些信息，用[L,R]表示下标从 $L$ 到 $R$ 的这些点。

线段树的用处就是，对编号连续的一些点进行修改或者统计操作，修改和统计的复杂度都是 $O(log2(n))$。

线段树的原理，就是将[1,n]分解成若干特定的子区间(数量不超过 $4\cdot n$)，然后将每个区间[L,R]都分解为少量特定的子区间，通过对这些少量子区间的修改或者统计，来实现快速对[L,R]的修改或者统计。

由此看出，用线段树统计的东西，必须符合区间加法，否则，不可能通过分成的子区间来得到[L,R]的统计结果。

符合区间加法的例子：

• 数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和

• 最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );

• 最大值——总最大值=max(左区间最大值，右区间最大值)

不符合区间加法的例子：

• 众数——只知道左右区间的众数，没法求总区间的众数

• 01序列的最长连续零——只知道左右区间的最长连续零，没法知道总的最长连续零

一个问题，只要能化成对一些连续点的修改和统计问题，基本就可以用线段树来解决了

2、原理 & 结构

线段树是一种基于分治思想的二叉树结构，用于在区间上进行信息统计。与树状数组相比，线段树是一种更加通用的结构：

1. 线段树的每个节点代表一个区间

2. 线段树具有唯一的根节点，代表的区间是整个统计范围,如 [1,N]

3. 线段树的每个叶节点都代表一个长度为1的元区间 [x,x]。

4. 对于每个内部节点[l,r],它的左子节点是[l,mid]，右子节点是[mid+1,r]，其中 $mid=\lfloor (l+r)/2\rfloor$。

• 区间视角

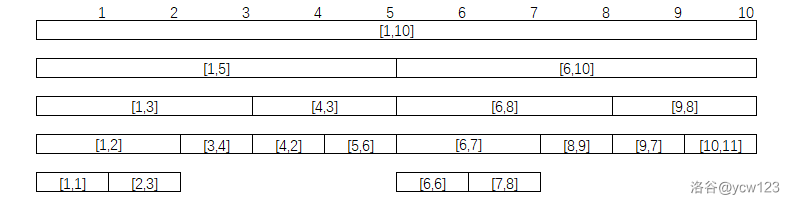
• 二叉树视角

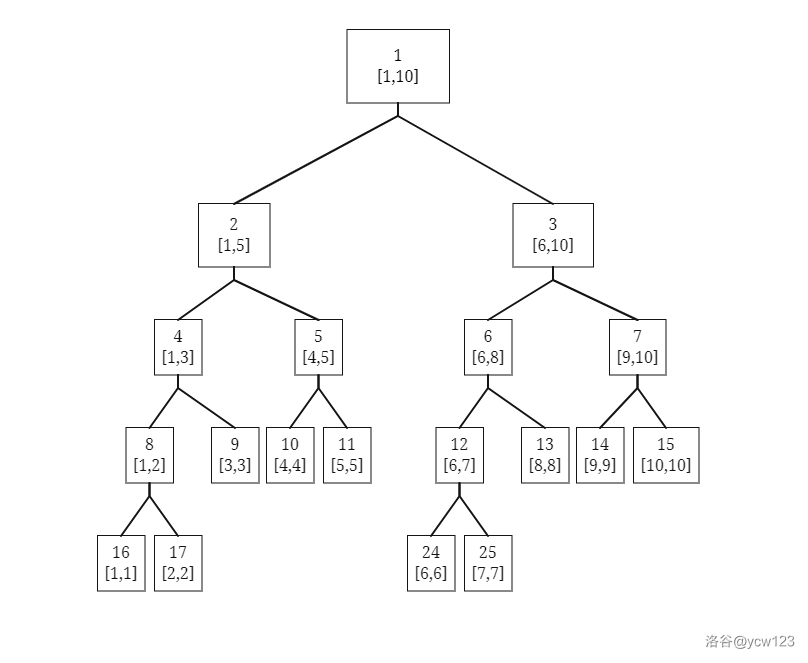
上图展示了一棵线段树。可以发现，去除树的最后一层，整棵线段树一定是一颗完全二叉树，树的深度为 $O(log2(n))$。因此我们可以按照与二叉堆类似的 “父子2倍”节点编号 方法：

1. 根节点编号为1。
2. 编号为 $x$ 的节点的左子节点编号为 $2\cdot x$ ,右子节点编号为 $2\cdot x+1$。

这样一来我们就能简单的使用一个 struct 数组来保存线段树。当然，树的最后一层节点在数组中保存的位置不是连续的，直接空出数组中多余的位置即可。

在理想情况下，$N$ 个叶节点的满二叉树有 $N+N/2+N/4+\dots +2+1=2N-1$ 个节点。因为在上述存储方式下，最后还有一层产生了空余，所以 保存线段树的数组长度要不小于 $4N$ 才能保证不会越界。

3、实现

• 线段树的建树

线段树的基本用途是对序列进行维护，支持查询与修改指令。

给定一个长度为 $N$ 的序列 $A$，我们可以在区间[1,N]上建立一颗线段树,每个叶节点[i,i]保存 $A_i$ 的值。线段树的二叉树结构可以很方便的从下往上传递信息。以区间和问题为例，记

$$sum(l,r)=\sum _{i=l}^r{A}_i$$

显然 $sum(l,r)=sum(l,mid)+sum(mid+1,r)$

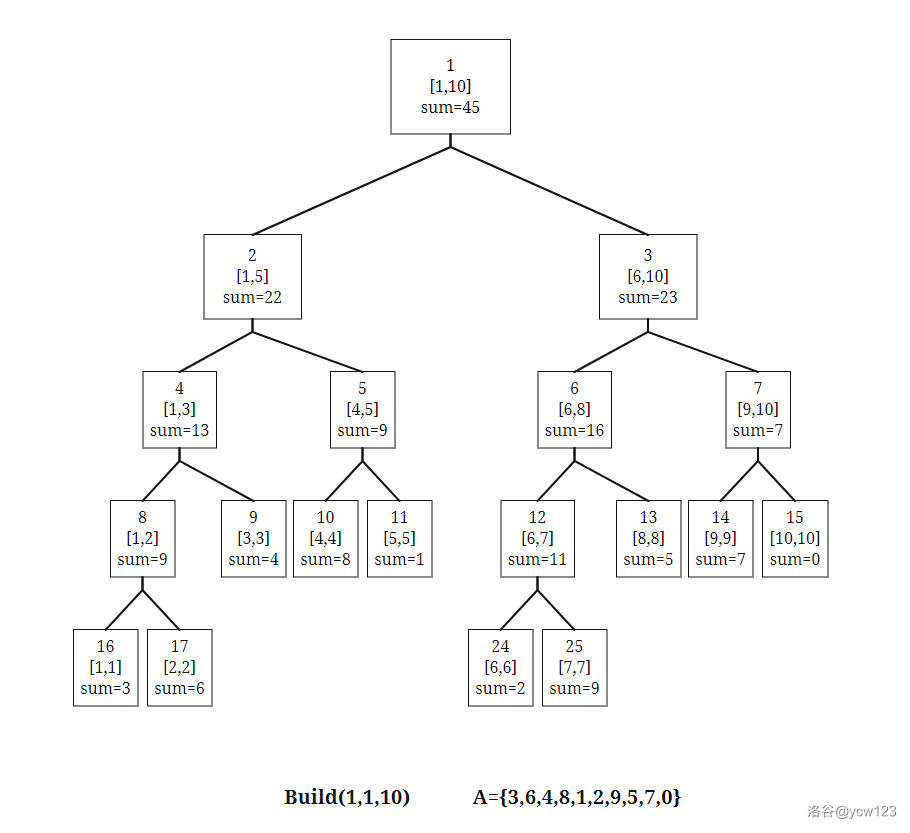
下面这段代码建立了一颗线段树并在每个节点上保存了对应区间的最大值。

struct Tree {
	int l,r;
	int sum;
} t[SIZE*4]; //struct数组存储线段树
 
void Pushup(int x){
	t[x].sum = t[x*2].sum + t[x*2+1].sum;
} 

void build(int x, int l, int r) {
	t[x].l = l, t[x].r = r;                  //节点x代表区间[l,r] 
	if (l==r) { t[x].sum = a[l]; return; }   //叶节点 
	int mid = (l + r) / 2;                   //折半 
	build(x*2, l, mid);           //左子节点[l,mid],编号 x*2 
	build(x*2+1, mid+1, r);       //右子节点[mid+1,r],编号 x*2+1 
	Pushup(x);                    //更新函数，从下往上传递信息 
}

build(1, 1, n);  //调用入口

• 线段树的单点修改

单点修改是形如“ C p k ”的指令，表示把 $A_p$ 的值增加 k。

在线段树中，根节点（编号为1的节点）是执行各种指令的入口。我们需要从根节点出发，递归找到代表区间 [p,p] 的叶节点，然后从下往上更新 [p,p] 以及它的所有祖先节点上保存的信息，如下图所示。时间复杂度为 O(log2(N))。

void Pushup(int x){        //更新信息函数
	t[x].sum = t[x*2].sum + t[x*2+1].sum;
} 

void updata(int x,int p,int k){
	if (t[x].l == t[x].r) { t[x].sum += k; return; } //找到叶节点
	int mid = (t[x].l + t[x].r) / 2;
	if (p <= mid) updata(x*2,p,k);           //x属于左半区间 
	else  updata(x*2+1,p,k);                 //x属于右半区间 
	Pushup(x);                               //从下往上更新信息 
}

updata(1,p,k); 

• 线段树的区间查询

区间查询是形如一条“Q l r”的指令，例如查询序列A在区间 [l,r] 上的和。我们只需要从根节点开始，递归执行以下过程：

1. 若 [l,r] 完全覆盖了当前节点代表的区间，则立即回溯，并且答案加上该节点的sum值。
2. 递归访问两个子节点，若与 [l,r] 无交集，则立即回溯，返回零。

int query(int x, int l, int r){
	if (t[x].l > r || t[x].r < l) return 0;          //与[l,r]无交集
	if (t[x].l >= l && t[x].r <= r) return t[x].sum; //完全包含 
	return query(x*2, l, r) + query(x*2+1, l, r);   //递归两个子节点 
}

printf("%d\n",query(1,l,r))  //调用入口 

该查询过程会把询问区间 [l,r] 在线段树上分成 $O(log2(N))$ 个节点，取它们的和作为答案。

为什么是 $O(log2(N))$ 个呢？仔细分上述过程，在每个节点 [pl,pr] 上，设 $mid=\lfloor (pl+pr)/2\rfloor$，可能会出现以下几种情况:

1. $l\le pl\le pr\le r$，即完全覆盖了当前节点，直接返回。

2. $pl\le l\le pr\le r$，即只有 $l$ 处于节点之内。

   (1). $l>mid$，只会递归右子树。

   (2). $l\le mid$，虽然递归两棵子树，但是右子点会在递归后直接返回。

3. $l\le pl\le r\le pr$，即只有 $r$ 处于节点之内，与情况2类似。

4. $pl\le l\le r\le pr$，即 $l$ 与 $r$ 都位于节点之内。

   (1). $l,r$ 都位于 $mid$ 的一侧，只会递归一棵子树。

   (2). $l,r$ 分别位于 $mid$ 的两侧，递归左右两棵子树。

也就是说，只有情况4(2)会真正产生对左两棵子树的递归。

请读者思考，这种情况至多发生一次，之后在子节点上就会变成情况2或3。

因此，上述查询过程的时间复杂度为 $O(2\times log2(N))=O(log2(N))$。

从宏观上解，相当于 $l,r$ 两个端点分别在线段树上划分出一条递归访问路径，情况4(2)在条路径于从下往上的第一次交会处产生。至此，线段树已经能够处理区间和问题，并且还支持动态修改某个数的值。

• 线段树的区间修改

在线段树的“区间查询”指令中,每当遇到被问区间 [l,r] 完全覆盖的节点时可以立即把该节点上存储的信息回溯。我们已经证明，被询问区间 [l,r] 在线段树上会被分成 $O(log2(N))$ 个小区间，从而在 $O(log2(N))$ 的时间内求出答案。

不过，在“区间修改”指令中，如果某个节被修改区间 [l,r] 完全覆盖，那么以该节点为根的整棵子树中的所有节点存储的信息会发生变化，若逐一进行更新，将使得一次区间修改指令的时间复杂度增加到 $O(N)$，这是我们不能接受的。

试想，如果我们在一次修改指令中发现节点代表的区间 [pl,pr] 被修改区间 [l,r] 完全覆盖,并且逐一更新了子树 $p$ 中的所有节点，但是在之后的查询指令中却根本没有用到 [l,r] 的子区间作为候选答案，那么更新 $p$ 的整棵子树就是徒劳的。

换言之，我们在执行修改指令时，同样可以在 $l\le pl\le pr\le r$ 的情况下立即返回。只不过在回溯之前向节点 $p$ 增加一个标记，即“该节点曾经被修改,但其子节点尚未被更新”。

如果在后续的指令中，需要从节点 $p$ 向下递归我们再检查 $p$ 是否具有标记。若有标记，就根据标记信息更新 $p$ 的两个子节，同时为 $p$ 的两个子节点增加标记然后清除 $p$ 的标记。

也就是说，除了在修改指令中直接划分成的 $O(log2(N))$ 个节点之外，对任意节点的修改都延迟到 “在后续操作中递归进入它的父节点时” 再执行。

这样一来，每条查询或修改指令的时间复杂度都降低到了 $O(log2(N))$ 。这些标记被称为“延迟标记”。

延迟标记提供了线段树中从上往下传递信息的方式。这“延迟”也是设计算法与解决问题的一个重要思路。

标记有相对标记和绝对标记之分：

相对标记是将区间的所有数 $+a$ 之类的操作，标记之间可以共存，跟打标记的顺序无关（跟顺序无关才是重点）。

所以，可以在区间修改的时候不下推标记，留到查询的时候再下推。

注意：如果区间修改时不下推标记，那么Pushup函数中，必须考虑本节点的标记。而如果所有操作都下推标记，那么Pushup函数可以不考虑本节点的标记，因为本节点的标记一定已经被下推了（也就是对本节点无效了）

绝对标记是将区间的所有数变成 $a$ 之类的操作，打标记的顺序直接影响结果，所以这种标记在区间修改的时候必须下推旧标记，不然会出错。

注意：有多个标记的时候，标记下推的顺序也很重要，错误的下推顺序可能会导致错误。

再以区间求和为例：

void Pushdown(int x){          //下推标记函数
	t[x*2].add += t[x].add;
	t[x*2+1].add += t[x].add;
	t[x*2].sum += t[x].add*(t[x*2].r - t[x*2].l + 1);
	t[x*2+1].sum += t[x].add*(t[x*2+1].r - t[x*2+1].l + 1);
	t[x].add=0;
}

void updata(int x, int k, int l, int r){
	if(l>t[x].r||r<t[x].l) return;           //无交集 
	if(l<=t[x].l&&r>=t[x].r){                //完全包含 
		t[x].add += k;
		t[x].sum += (t[x].r - t[x].l + 1) * k;
		return;
	}
	Pushdown(x);                             //下推标记 
	updata(x*2, k, l, r);
	updata(x*2+1, k, l, r);
	Pushup(x);                               //从下往上更新信息 
}

完整代码：

#include<bits/stdc++.h>
using namespace std; 
const int SIZE=1e5;
struct Tree {
	int l,r;
	int sum;
	int add;
} t[SIZE*4]; //struct数组存储线段树
int n,a[SIZE];
void Pushup(int x){
	t[x].sum = t[x*2].sum + t[x*2+1].sum;
} 
void Pushdown(int x){
	t[x*2].add += t[x].add;
	t[x*2+1].add += t[x].add;
	t[x*2].sum += t[x].add*(t[x*2].r - t[x*2].l + 1); 
	t[x*2+1].sum += t[x].add*(t[x*2+1].r - t[x*2+1].l + 1);
	t[x].add=0;
}
void build(int x, int l, int r) {
	t[x].l = l, t[x].r = r;                  //节点x代表区间[l,r] 
	if (l==r) { t[x].sum = a[l]; return; }   //叶节点 
	int mid = (l + r) / 2;                   //折半 
	build(x*2, l, mid);           //左子节点[l,mid],编号 x*2 
	build(x*2+1, mid+1, r);       //右子节点[mid+1,r],编号 x*2+1 
	Pushup(x);                    //更新函数，从下往上传递信息 
}

void updata(int x, int k, int l, int r){
	if(l>t[x].r||r<t[x].l) return;           //无交集 
	if(l<=t[x].l&&r>=t[x].r){                //完全包含 
		t[x].add += k;
		t[x].sum += (t[x].r - t[x].l + 1) * k;
		return;
	}
	Pushdown(x);                             //下推标记 
	updata(x*2, k, l, r);
	updata(x*2+1, k, l, r);
	Pushup(x);                               //从下往上更新信息 
}
int query(int x,int l,int r){
	int res=0;
	if(l>t[x].r||r<t[x].l) return 0;           //无交集
	if(l<=t[x].l&&r>=t[x].r) return t[x].sum;    //完全包含
	Pushdown(x);                               //下推标记 
	res= query(x<<1,l,r)+query(x<<1|1,l,r);    //累计答案 
	Pushup(x);                                 //从下往上更新信息
	return res;                                //回溯 
}

by 2021.7.29