本书中的约瑟夫问题定义如下:从围成标有记号1到n的圆圈的n个人开始,每隔一个删去一个人,知道只有一个人幸存下来。
下图是n=10的起始图形:

削去的顺序为2,4,6,8,10,3,7,1,9,于是最后有5幸存下来。问题是对总人数为n时,幸存者的号码J(n)是多少?
首先面对这个问题的时候,由于题目数据比较少,我们会来时一步一步的推导,第一次循环的时候,从2开始削去了环中的所有偶数,所以我们知道了最后题目的结果肯定是一个奇数。随着一轮一轮的循环删除在环中的数据规模不断缩小,所以我们把它抽象成如下形式:
我们假设一开始有2n个人,经过第一轮消除所有偶数之后编程如下形式:
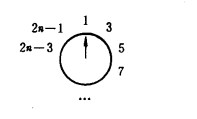
下一个离开的就是3号(因为上一个删除了2n),对比开始没有进行删除的情况我们可以知道,按顺序删除的每个数据变成了之前的数据加倍再减去一,就是说
J(2n)=2J(n)-1,n>=1.
下面再来考虑对于奇数的情形,对于2n+1个人,标号为1的人恰好在标号为2n的人之后被删除,我们类比2n的情形可以得到
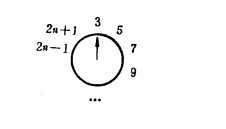
J(2n+1)=2J(n)+1,n>=1.
将以上的方程和J(1)=1组合起来就可以得到在所有情形下定义J的递归式:
J(1)=1.
J(2n)=2J(n)-1,n>=1.
J(2n+1)=2J(n)+1,n>=1.
为了能够在有限次运算内求得指定的J(n),我们来将递归式求得封闭形式:
对一个递归式,发现规律的最好方法就是将数据打表

我们发现表中的数据以2的幂将表分组(1,2,4,8…),并且每一组中的数据都是在递增2。所以我们可以讲n表示成n=2^m+l,m是使2^m不超过n的最大幂次,l表示在每一个分组中所占的位置,此时的递归式的解可以表示为
J(2^m +l)=2*l+1,m>=0,0<=l<2^m.
下面给出上式的证明,我们对m使用归纳法:当m=0时必定有l=0,所以上式的基础就是J(1)=1,此结论为真。归纳证明分为l是偶数还是奇数,如果m>0并且2^m+l=2n,那么l是偶数,那么根据归纳假设有:
J(2^m+l)=2J(2^(m-1)+l/2)-1=2l+1.
这就是我们想要的结果。当2^m=2n+1为奇数,我们同样有类似的证明成立。
我将在下一篇文章中给出文中递推式的推广,这些探讨将会解释所有这类问题背后的隐藏结构。






















 8711
8711

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








