Strassen’s algo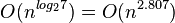rithm for matrix multiplication

Strassen算法能够在时间内完成。

package chapter4;

import Utils.P;

class Matrix {
	private int[][] data;
	int lengthX;
	int lengthY;
	private int xs;
	private int ys;

	public Matrix(int[][] data) {
		this.data = data;
		lengthX = data.length;
		lengthY = data[0].length;
		this.xs = this.ys = 0;
	}

	Matrix(int[][] data, int xs, int xe, int ys, int ye) {
		this.data = data;
		this.xs = xs;
		this.ys = ys;
		this.lengthX = xe - xs;
		this.lengthY = ye - ys;
	}

	public Matrix subMatrix(int xs, int xe, int ys, int ye) {
		return new Matrix(data, xs, xe, ys, ye);
	}

	public int get(int x, int y) {
		return data[xs + x][ys + y];
	}

	public void set(Matrix mt) {
		for (int i = 0; i < mt.lengthX; i++) {
			for (int j = 0; j < mt.lengthY; j++) {
				set(mt.get(i, j), i, j);
			}
		}
	}

	public void set(int d, int x, int y) {
		this.data[xs + x][ys + y] = d;
	}

	public Matrix minus(Matrix m) {
		if (m.lengthX != lengthX || m.lengthY != lengthY) {
			try {
				throw new Exception();
			} catch (Exception e) {
				// TODO Auto-generated catch block
				e.printStackTrace();
				System.exit(0);
			}
		}
		Matrix ret = new Matrix(new int[lengthX][lengthY]);
		for (int i = 0; i < lengthX; i++) {
			for (int j = 0; j < lengthY; j++) {
				ret.set(get(i, j) - m.get(i, j), i, j);
			}
		}
		return ret;
	}

	public Matrix sub(Matrix m) {
		if (m.lengthX != lengthX || m.lengthY != lengthY) {
			try {
				throw new Exception(m.lengthX + " " + lengthX + " " + m.lengthY
						+ " " + lengthY);
			} catch (Exception e) {
				// TODO Auto-generated catch block
				e.printStackTrace();
				System.exit(0);
			}
		}
		Matrix ret = new Matrix(new int[lengthX][lengthY]);
		for (int i = 0; i < lengthX; i++) {
			for (int j = 0; j < lengthY; j++) {
				ret.set(get(i, j) - m.get(i, j), i, j);
			}
		}
		return ret;
	}

	public Matrix add(Matrix m) {
		if (m.lengthX != lengthX || m.lengthY != lengthY)
			return null;
		Matrix ret = new Matrix(new int[lengthX][lengthY]);
		for (int i = 0; i < lengthX; i++) {
			for (int j = 0; j < lengthY; j++) {
				ret.set(get(i, j) + m.get(i, j), i, j);
			}
		}
		return ret;
	}

	public void print() {
		for (int i = xs; i < xs + lengthX; i++) {
			for (int j = ys; j < ys + lengthY; j++) {
				P.rint(data[i][j]);
				P.rint(" ");
			}
			P.rintln();
		}
	}
}

public class Strassen {

	public static Matrix strassen(Matrix a, Matrix b) {
		Matrix c = new Matrix(new int[a.lengthX][b.lengthY]);
		if (a.lengthX == 1 && a.lengthY == 1) {
			c.set(a.get(0, 0) * b.get(0, 0), 0, 0);
			return c;
		}
		int mx = a.lengthX / 2;
		int my = a.lengthY / 2;
		Matrix a11 = a.subMatrix(0, mx, 0, my);
		Matrix a12 = a.subMatrix(0, mx, my, b.lengthY);
		Matrix a21 = a.subMatrix(mx, a.lengthX, 0, my);
		Matrix a22 = a.subMatrix(mx, a.lengthX, my, a.lengthY);
		Matrix b11 = b.subMatrix(0, mx, 0, my);
		Matrix b12 = b.subMatrix(0, mx, my, b.lengthY);
		Matrix b21 = b.subMatrix(mx, b.lengthX, 0, my);
		Matrix b22 = b.subMatrix(mx, b.lengthX, my, b.lengthY);
		Matrix c11 = c.subMatrix(0, mx, 0, my);
		Matrix c12 = c.subMatrix(0, mx, my, c.lengthY);
		Matrix c21 = c.subMatrix(mx, c.lengthX, 0, my);
		Matrix c22 = c.subMatrix(mx, c.lengthX, my, c.lengthY);

		Matrix s1 = b12.sub(b22);
		Matrix s2 = a11.add(a12);
		Matrix s3 = a21.add(a22);
		Matrix s4 = b21.sub(b11);
		Matrix s5 = a11.add(a22);
		Matrix s6 = b11.add(b22);
		Matrix s7 = a12.sub(a22);
		Matrix s8 = b21.add(b22);
		Matrix s9 = a11.sub(a21);
		Matrix s10 = b11.add(b12);

		Matrix p1 = strassen(a11, s1);
		Matrix p2 = strassen(s2, b22);
		Matrix p3 = strassen(s3, b11);
		Matrix p4 = strassen(a22, s4);
		Matrix p5 = strassen(s5, s6);
		Matrix p6 = strassen(s7, s8);
		Matrix p7 = strassen(s9, s10);

		c11.set(p5.add(p4).sub(p2).add(p6));
		c12.set(p1.add(p2));
		c21.set(p3.add(p4));
		c22.set(p5.add(p1).sub(p3).sub(p7));
		return c;
	}

	public static void main(String[] args) {
		Matrix mt = new Matrix(new int[][] { { 1, 3 }, { 7, 5 } });
		Matrix mt2 = new Matrix(new int[][] { { 6, 8 }, { 4, 2 } });
		Strassen.strassen(mt, mt2).print();
	}
}