二叉搜索----BST

 二叉搜索树（binary search tree， BST），它的每个内部结点都关联一个关键字，并且具有以下性质：

任意结点的关键字都大于（或等于）该节点的左子树的关键字，小于（或等于）右子树的关键字。

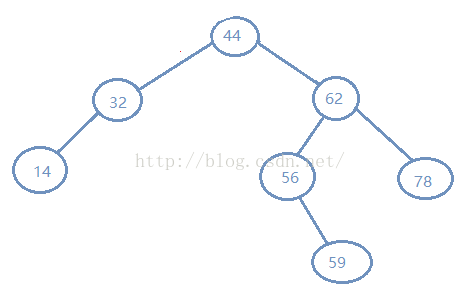
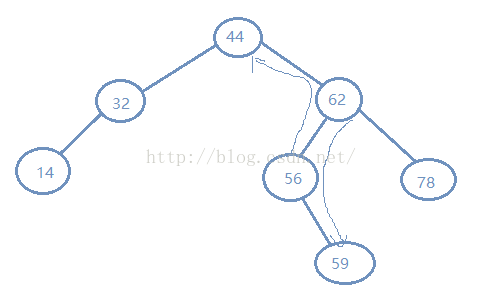
如图示就是一颗二叉搜索树

二叉搜索树的遍历由关键字的有序性可通过输的中序遍历将其按顺序输出
中序的递归遍历

void Order_Travarsal_Tree(BiTree root){
       BiTree p;
       p=root;
       if(p->next != NULL){
          Order_Travarsal_Tree(p->Child);
          Visit(p->data);
          Order_Travarsal_Tree(p->Rchild);
   }
}

中序非递归遍历

void Order_Travarsal_Tree(BiTree root){
       SeqStack *S;
       BiTree p;
       InitStack(S); p=root;
       while(p != NULL  || !IsEmpty(S)){
            while(p != NULL ){
                Push(S,&p);
            }
            if(!IsEmpty(S)){
               Pop(S,&p);
               Visit(p->data);
               Push(S,&p->Rchild);
            }
       }
}

查询二叉查找树

在查询二叉查找树是按照所给的key沿着根结点通过与各个节点的比较往下走，如果有节点键值与key相等则停止，否则一直向下查找，直到结点为空

递归查找

BiTree Search_BiTree(BiTree root, <span style="font-family: Arial, Helvetica, sans-serif;">BiTree</span> key){
      BiTree p=root;
      if(!p && p == key)
        return p;
      else if(p->data > key->data)
        return Search_BiTree(p->Lchild,key);
      else
        return Search_BiTree(p->Rchild, key)
}

非递归查找

BiTree Search_BiTree(BiTree root BiTreekey){
      BiTree p=root;
      while(!p){
          if(p->data == key->deta)
               return p;
          else  if(p->data > key->data)
                p=p->Lchild;
          else
                p=p->Rchild;      
      }
      return NULL;
}

二叉查找树的前趋和后继

在讨论前趋和后继之前先了解一下怎样求二叉搜索树的最大值和最小值

  求最大值，即沿着根结点向书的右子树遍历，直到结点右子树为空

BiTree Max_BiTree(BiTree root){
        BiTree p=root;
        while(p->Rchild != NULL){
         p=p->Rchild;
        }
        return p;
}

求最小值，即沿着根结点向书的左子树遍历，直到结点左子树为空

BiTree Min_BiTree(BiTree root){
        BiTree p=root;
        while(p->Lchild != NULL){
         p=p->Lchild;
        }
        return p;
}

后继

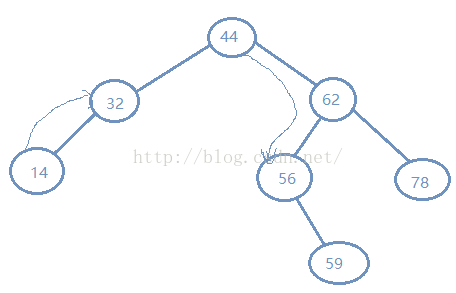
要查找如图示 14 和 44 的后继 14-> 32,44->56

BiTree BiTree_Suceed(BiTree root){
        BiTree p=root;
        if(p->Rchild != NULL)
          return Min_BiTree(p->Rchild);
        BiTree q;
        q=p->parent;
        if(p == q->Lchild)
            return q;
         while(q->parent != NULL){            
             q=q->parent;
         }
          return q;
}

前趋

要查找如图示 56 和 62 的 前趋56->44,62->59

BiTree BiTree_Precursor(BiTree root){
        BiTree p=root;
        if(p->Lchild != NULL)
          return Max_BiTree(p->Lchild);
        BiTree q;
        q=p->parent;
        if(p == q->Rchild)
            return q;
         while(q->parent != NULL){            
             q=q->parent;
         }
          return q;
}

二叉搜索树的插入和删除

插入

在二叉搜索树中插入就是寻找合适的地方，结点比键值大就向右子树遍历，直到结点右子树为空，然后将结点插入，反之向左；

<pre name="code" class="cpp">void BiTree_Insert(BiTree root, BiTree value){
	BiTree p=root;
	if(root == NULL){
		root=value;		
		return 
	}
	while(!p){
		if(p->key > value->key)
			p=p->Lchild;
		else
			p=p->Rchild;
	}
	if(p->key > value->key)
		p->Lchild=value;
	else
		p->Rchildvalue;
}

删除

在二叉搜索树的删除中分三种情况，分别是所删结点有有左子树或右子树、左右子树都存在和无子树三种情况

对于无左右子树的情况 直接删除就行了，无需讨论下面来看看其他两种情况

有两个孩子

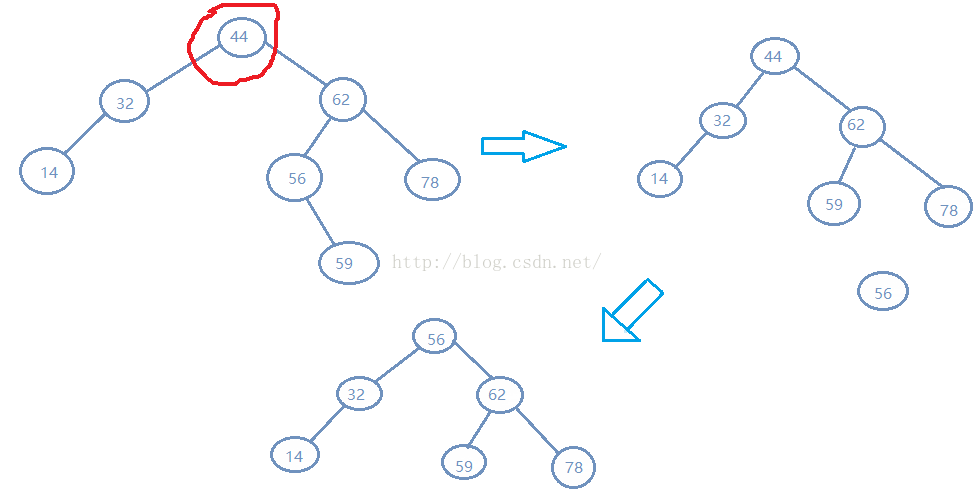
当结点有两个孩子时，不会直接删掉当前结点 ,而是找到当前结点的后继结点，用后继结点的关键字替换掉当前结点的关键字，并且删掉后继结点，如上图。因为后继结点的右子树的最小关键字，用 后继替换当前结点 ,就依然能保证删除位置的左子树偏小，右子树偏大的性质

只有一个孩子

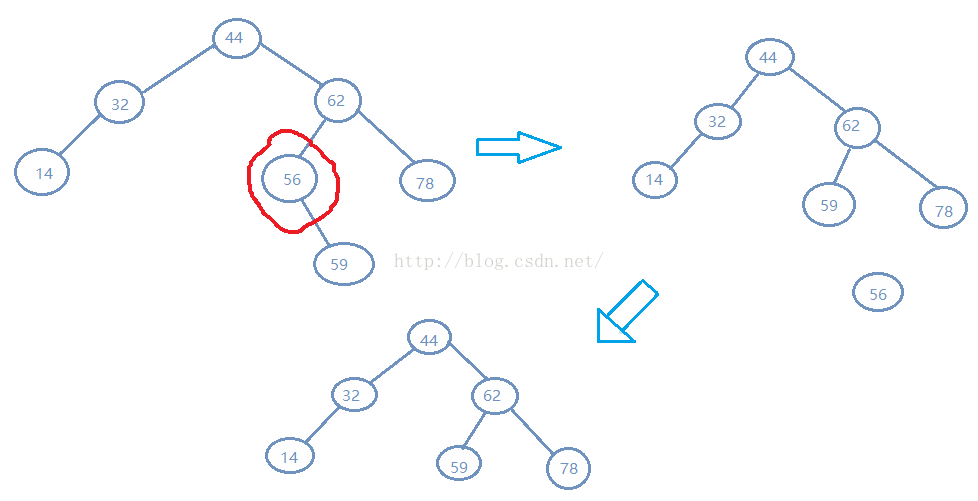
BiTree BiTree_delete(BiTree root ,BiTree D_key){
	BiTree p,q;
	p=BiTree_Search(root,D_key);
	if(p->Lchild == NULL && p->Rchild == NULL){
		q=p;
	}else if(p->Lchild == NULL  || p->Rchild == NULL){
		if(p==p->parent->Lchild)
			p->parent->Lchild=(p->Lchild == NULL ) ? p->Rchild : p->Lchild ;
		else
			p->parent->Rchild=(p->Lchild == NULL ) ? p->Rchild : p->Lchild ;
		p=q;
	}else{
		q=BiTree_Succeed(p);
		p=q;
		if(q->Rchild != NULL)
			q->parent-Lchild=q->Rchild;
	}
	
	free(q);
	return p;
}